【數據結構之二叉樹】二叉樹的創建及遍歷實現
0. 前言
前文【二叉樹的概念和原理】主要介紹了樹的相關概念和原理,本文主要內容為二叉樹的創建及遍歷的代碼實現,其中包括遞歸遍歷和棧遍歷。
1. 二叉樹的實現思路
1.0. 順序存儲——數組實現
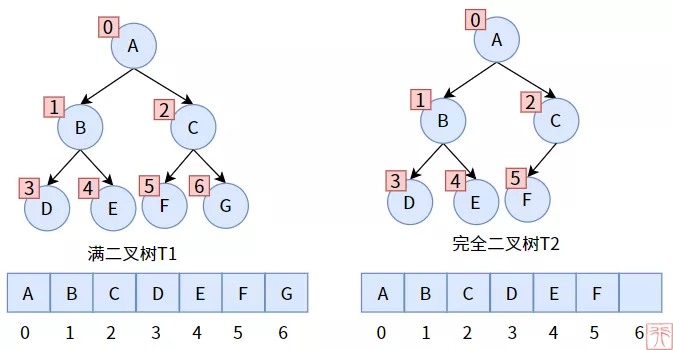
前面介紹了滿二叉樹和完全二叉樹,我們對其進行了編號——從 0 到 n 的不中斷順序編號,而恰好,數組也有一個這樣的編號 —— 數組下標,只要我們把二者聯合起來,數組就能存儲二叉樹了。
那么非滿、非完全二叉樹怎么使用數組存儲呢?
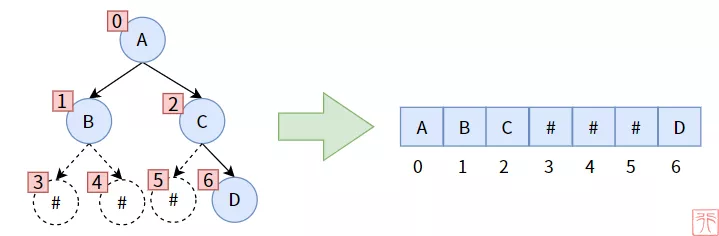
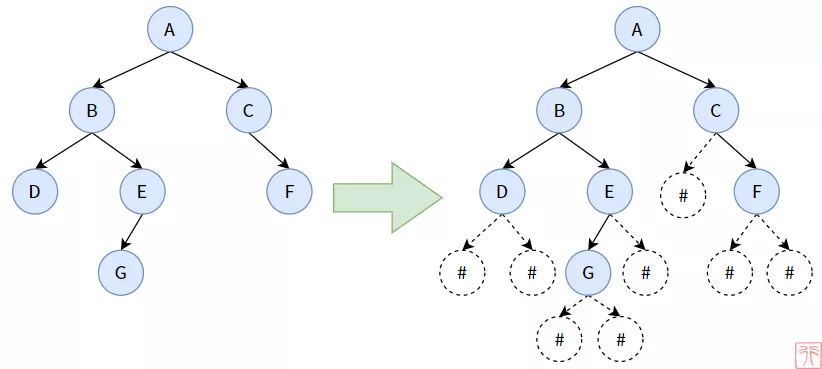
我們可以在二叉樹中補上一些虛構的結點,構造出來一個滿/完全二叉樹來,存儲到數組中時,虛構的結點對應的數組元素不存儲數據(# 代表虛構的不存在)。如下圖:
這樣存儲的缺點是,數組中可能會有大量空間未用到,造成浪費。
1.1. 鏈式存儲——鏈表實現
我們畫樹的圖時,采用的都是結點加箭頭的方式,結點表示數據元素,箭頭表示結點之間的關系,清晰明了。如果你對鏈表熟悉,那么肯定能覺察到這是典型的鏈式結構。鏈式結構完美解決了順序結構中可能會浪費空間的缺點,而且也不會有數組空間限制。
下面來分析一下結點的結構。
樹的結點包括一個數據元素和若干指向其子樹分支。二叉樹的結點相對簡單,包括:
- 數據元素
- 左子樹分支(結點的左孩子)
- 右子樹分支(結點的右孩子)
怎么來實現呢?單鏈表的結點是使用一個指向其后繼結點的指針來表示其關系的。同樣地,我們也可以使用指針來表示結點和其左孩子、右孩子的關系。
分析到這,二叉樹的結點就清晰了:
- 一個存儲數據的變量——data
- 一個指向其左孩子結點的指針——left_child
- 一個指向其右孩子結點的指針——right_child
用 C 語言的結構體實現二叉樹的結點(為了方便起見,我們的數據全為字符類型):
- /*二叉樹的結點的結構體*/
- typedef struct Node {
- char data; //數據域
- struct Node *left_child; //左孩子指針
- struct Node *right_child; //右孩子指針
- } TreeNode;
2. 二叉樹的創造
二叉樹的定義是遞歸的定義,所以如果你想要創造一個二叉樹,也可以借助遞歸去創造。如何遞歸創造呢?在現實中,一棵樹先長根、再長枝干、最后長葉子。我們用代碼創造樹時,也遵守這個原則,即先創造根結點,然后左子樹,最后右子樹。整個過程和先序遍歷相似。
我以前寫過的文章中有二叉樹創建過程的動態圖[1],這里不再贅述。
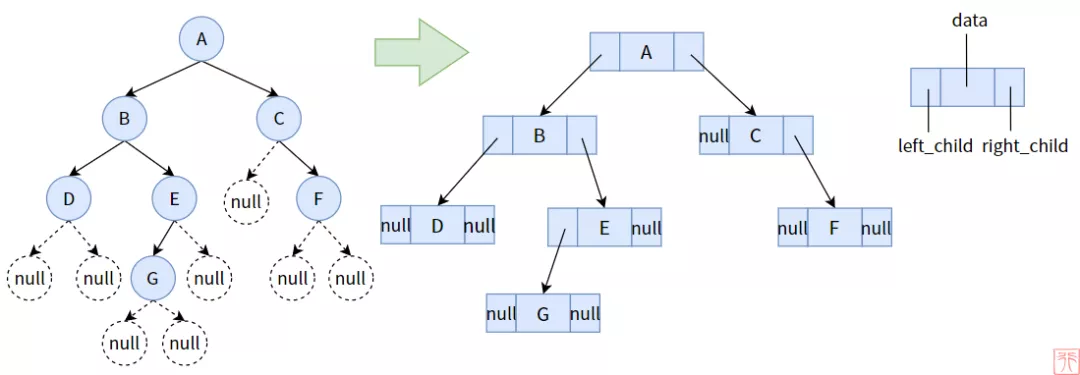
這里以創造下圖中的樹為例:
說明:當我們看到如左圖的二叉樹時,要立即能腦補出對應的右圖。#結點是什么?
前面我們已經畫出了類似的圖,當時是 NULL 結點,它的作用是標識某個結點沒有孩子,它是我們虛構出來的。在實際使用 C 語言創造二叉樹時,需要使用 #或者什么其他的符號來代替 NULL.
上圖的先序遍歷順序為:ABDEGCF,如果加上 # 結點,則為:ABD##EG###C#F##. 我們按照此順序來創造二叉樹。
代碼如下:
- /**
- * 創造一個二叉樹
- * root: 指向根結點的指針的指針
- */
- void create_binary_tree(TreeNode **root)
- {
- char elem;
- scanf("%c", &elem);
- if (elem == '#') {
- *root = NULL;
- } else {
- *root = create_tree_node(elem); //創造一個二叉結點
- create_binary_tree(&((*root)->left_child));
- create_binary_tree(&((*root)->right_child));
- }
- }
請注意,函數 create_binary_tree 接受的是一個指向根結點的指針的指針,至于為什么要使用指針的指針,理由在介紹單鏈表的初始化時已經解釋了。
3. 二叉樹的遍歷
在文章【二叉樹的概念和原理】中已經介紹了遍歷的原理了,下面使用 C 語言實現它。
3.0. 遍歷實質
二叉樹的定義是遞歸的定義,即在二叉樹的定義中又用到了二叉樹的定義。所以無論是在創造二叉樹,還是在遍歷二叉樹,我們要做的只有三件事:訪問根結點、找左子樹、找右子樹。所謂先序、中序、后序遍歷,無非是這三件事的順序罷了。
3.1. 遞歸實現
我們如果使用遞歸代碼,很容易就能實現遍歷,而且代碼非常簡潔。
【先序遍歷】
- /**
- * 先序遍歷
- * root: 指向根結點的指針
- */
- void preorder_traversal(TreeNode *root)
- {
- if (root == NULL) { //若二叉樹為空,做空操作
- return;
- }
- printf("%c ", root->data); //訪問根結點
- preorder_traversal(root->left_child); //遞歸遍歷左子樹
- preorder_traversal(root->right_child); //遞歸遍歷右子樹
- }
【中序遍歷】
- /**
- * 中序遍歷
- * root: 指向根結點的指針
- */
- void inorder_traversal(TreeNode *root)
- {
- if (root == NULL) { //若二叉樹為空,做空操作
- return;
- }
- inorder_traversal(root->left_child); //遞歸遍歷左子樹
- printf("%c ", root->data); //訪問根結點
- inorder_traversal(root->right_child); //遞歸遍歷右子樹
- }
【后序遍歷】
- /**
- * 后序遍歷
- * root: 指向根結點的指針
- */
- void postorder_traversal(TreeNode *root)
- {
- if (root == NULL) { //若二叉樹為空,做空操作
- return;
- }
- postorder_traversal(root->left_child); //遞歸遍歷左子樹
- postorder_traversal(root->right_child); //遞歸遍歷右子樹
- printf("%c ", root->data); //訪問根結點
- }
事實上,大部分使用遞歸做的事,使用棧也可以做到。下面介紹遍歷的棧實現。
3.2. 棧實現
我們利用了棧的后進先出的特性,
棧實現的代碼較復雜,受篇幅限制,這里只介紹先序遍歷和后序遍歷,詳細代碼請移步至代碼倉庫查看。
【先序遍歷】
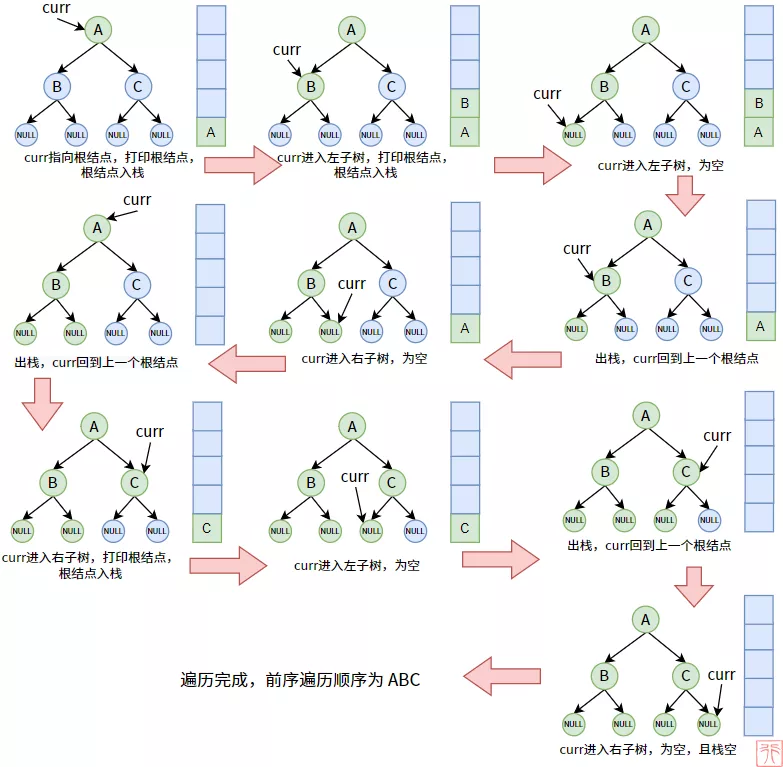
使用棧的先序遍歷
我們的樹的結點是要全部都入棧的(暫不管順序如何),那么入棧的條件是什么?就是該結點可以被看作某棵樹(子樹)的根結點的時候。即,curr 指針指向的結點一定為某顆樹(子樹)的根結點。
在【二叉樹的概念和原理】中,我們已經看到了,遍歷完某個子樹時,一定要回到其雙親結點。這種回溯如何實現?可以利用棧的先進后出、后進先出的特點,這個特點能在棧中完美保存結點在樹中父子關系,棧頂元素即為當前子樹的雙親結點。
- /**
- * 使用棧實現的先序遍歷
- */
- void preorder_traversal_by_stack(TreeNode *root)
- {
- //創造并初始化棧
- Stack stack;
- init_stack(&stack);
- TreeNode *curr = root; //輔助指針curr
- while (curr != NULL || !stack_is_empty(&stack)) {
- while (curr != NULL) {
- printf("%c", curr->data); //打印根結點
- push(&stack, curr); //根結點入棧
- curr = curr->left_child; //進入左子樹
- }
- if (!stack_is_empty(&stack)) {
- pop(&stack, &curr); //出棧,回到上一個根結點
- curr = curr->right_child; //進入右子樹
- }
- }
- }
【后序遍歷】
后序遍歷相較于前序和中序較為麻煩,不像前序和中序遍歷那樣。因為前序和中序的根結點在右子樹之前,所以我們可以在出棧的時候同時進行打印根結點和進入右子樹。
后序遍歷的根結點在右子樹之后,這就要求我們再遍歷完左子樹后,先返回到根結點,然后進入右子樹,遍歷完右子樹之后,再回到根結點,才能打印它。
關鍵之處還在于左子樹、右子樹、根結點的順序。
所以當 curr 指針遍歷完左子樹后,我們不能直接將根結點出棧,而是先從棧頂讀取到根結點,然后 curr 指針返回到根結點,然后 curr 指針進入右子樹進行遍歷,當右子樹遍歷完成后,將根結點出棧,才能打印根結點。
這樣一來,后序遍歷就有兩次回到根結點的動作,且這兩次的后續動作不一樣。第一次通過讀取棧頂回到根結點,然后進入右子樹;第二次通過出棧回到根結點,然后打印根結點。
這樣看似解決了后序遍歷的順序問題,但其實又得到了一個新的問題,即,我們如何知道右子樹被遍歷完了?
我們有兩次回到根結點的動作,對于寫代碼的人來說,我們知道兩次回到根結點之后該干什么,知道右子樹是否被遍歷完了。但是對于 curr 指針來說,它不知道,兩次回到根結點,它都不知道右子樹是否被遍歷完成了。
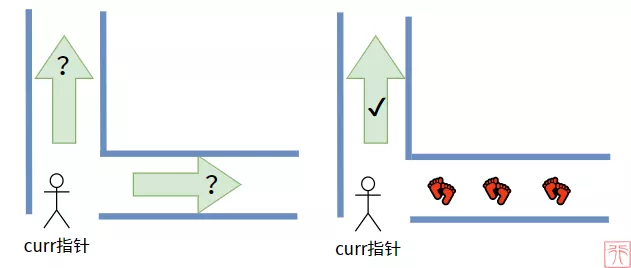
此時,對于curr 指針來說,就像有兩條路擺在它面前讓它選擇其中一條,它難以抉擇。如果當其中一條有過它的腳印,那么它就很容易選擇那條沒走過的路了。
所以我們現在還需要一個“腳印”指針——prev,prev指針用來記錄 curr訪問過的結點。
當 curr 指針第二次回到根結點的時候,一看,哦!我的腳印留在那呢!(prev指針指在右子樹那里)curr 指針就直接放心打印根結點了。
- /**
- * 使用棧實現的后序遍歷
- */
- void postorder_traversal_by_stack(TreeNode *root)
- {
- Stack stack;
- init_stack(&stack);
- TreeNode *curr = root; //輔助指針curr,記錄當前訪問結點
- TreeNode *prev = NULL; //腳印指針prev,記錄上一個訪問過的結點
- while (curr != NULL || !stack_is_empty(&stack)) {
- if (curr != NULL) {
- push(&stack, curr); //根結點入棧
- curr = curr->left_child; //進入左子樹
- } else {
- get_top(&stack, &curr); //讀棧頂元素,不是出棧
- //右子樹不為空,且右子樹沒被遍歷
- if (curr->right_child != NULL && curr->right_child != prev) {
- curr = curr->right_child; //進入右子樹
- push(&stack, curr); //根結點入棧
- curr = curr->left_child; //進入左子樹
- } else { //右子樹已被遍歷或者右子樹為空,可以打印根結點了
- pop(&stack, &curr); //根結點出棧
- printf("%c", curr->data); //打印根結點
- prev = curr; //記錄
- curr = NULL; //置空,進入下一輪循環
- }
- }
- }
- }
以上代碼中用到的棧的相關函數這里不再給出,詳細代碼請移步至代碼倉庫(文末獲取)。
4. 總結
遞歸的代碼雖然簡潔,但是對新手來說卻有點難以理解,這是因為接觸的太少。棧的代碼相對來說容易理解一些,但代碼比較復雜,特別是后序遍歷的代碼。
不過當你真正理解了二叉樹的定義、概念、原理之后,代碼相關的問題就不再是問題了,最終只落在六個字上——無他,惟手熟爾。
以上就是二叉樹的創建和遍歷的實現。
參考資料
[1]二叉樹創建過程的動態圖: https://blog.csdn.net/m0_47335900/article/details/106856321
[2]GitHub: https://github.com/xingrenguanxue/Simple-DS-and-Easy-Algo
[3]Gitee: https://gitee.com/xingrenguanxue/Simple-DS-and-Easy-Algo