Table Index

前面介紹完了 Hash Table，在數據庫系統中，它可以用于一些 sql 執行時的臨時數據結構，或者用來存儲一些元數據信息，也可以作為表的 Hash 索引，但是對于表索引，在更通用的場景下， B+ 樹是更廣泛的選擇。

表索引（Index）指的是表中數據的一些子集，這些子集能夠標識表中數據的一些特征，以便能夠快速的去查找 table 中的數據，并且數據庫能夠保證，表中數據和表索引數據的一致性。

B+ Tree 基本概念

B+ Tree 實際上是一種平衡樹結構，它能夠保證數據有序存儲，可以在平均 O(log n) 復雜度下查詢、插入、刪除數據。

它實際上類似二叉平衡樹，但是每個節點可以擁有不止 2 個子節點，并且能夠適配數據庫需要讀取整塊數據的需求，提升數據讀寫的效率。

B+ 樹是一個多叉平衡樹，例如 M 個分叉指的是每個 inner node 都有 M 個路徑到子節點，具有以下基本特征：

• 完全平衡的樹結構，即所有子節點到根節點的距離始終保持一致
• 除根節點外，每個節點的數據量至少大于 M 的一半，即 M/2-1 <= #keys <= M-1
• 每一個具有 k 個 key 的節點內，都有 k+1 個指向子節點的指針

下圖所示，是一個 B+ Tree 的例子。

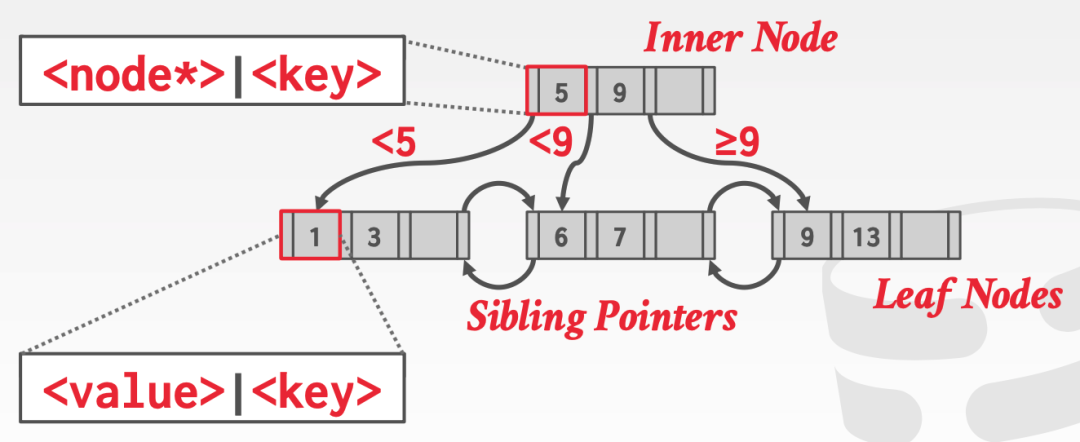
最底層的節點叫做 leaf node 葉子節點，上層的叫做 inner node，最頂層的 inner node 就是根節點（root node）。

inner node 中不會存儲實際的數據，而是存儲 key 以及指向其子節點的指針。

葉子節點之間有指針串聯，方便進行 scan 操作；每個葉子節點中存儲了實際的 key/value 數據。

葉子節點的內部結構，一般有兩種不同的布局方式，一種是很常見的，存儲一個 page id，并且將索引的 key 和 value 都存放到節點中，然后一個 page 指向下一個 page。

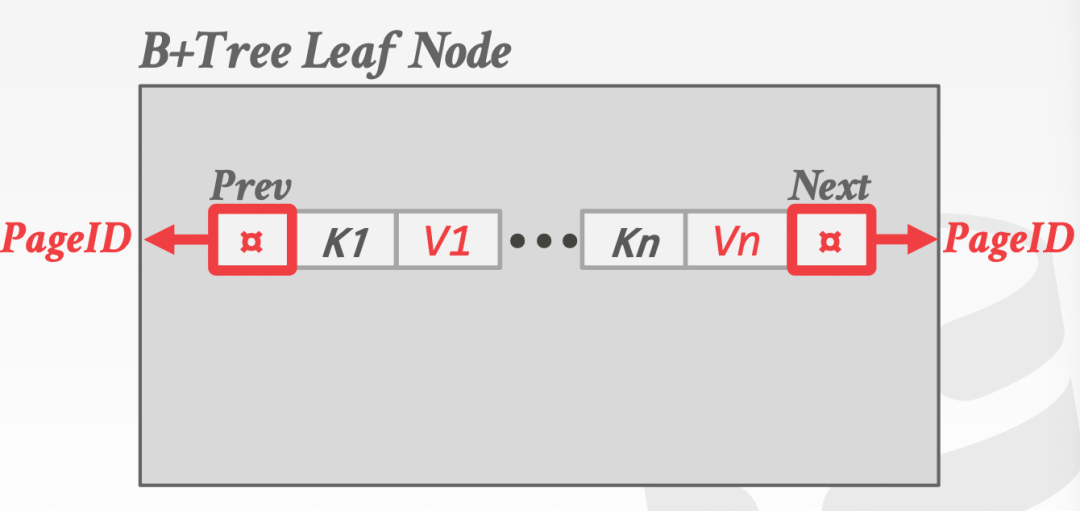
這樣是將 key/value 保存在了一起，并不利于順序掃描，如果我們只需要掃描 key 的話，那么會有一些額外的消耗。

另一種方式是將 key 和 value 分開，結構大致如下所示：

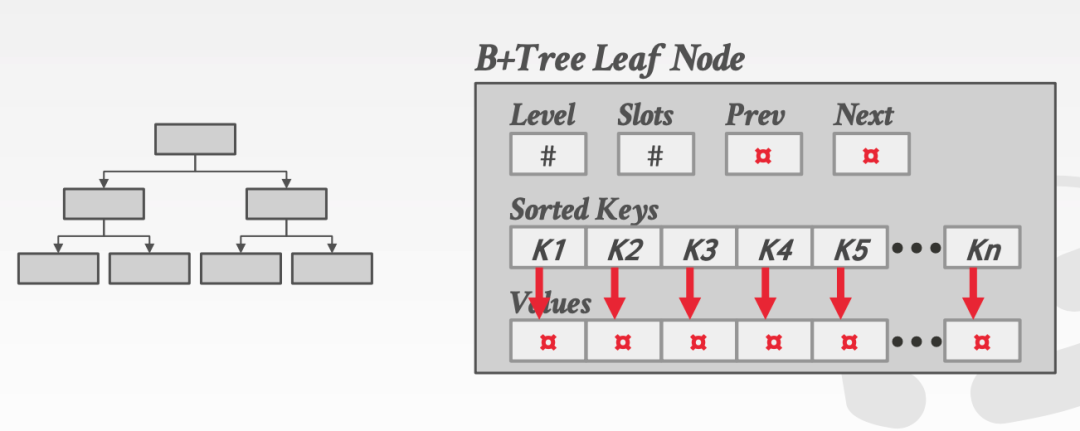
其中包含了一些元數據信息，例如當前的層數，空閑空間等，以及一個有序的 key 列表，并且每一個 key 指向了它自己的 value。

而實際 value 所表示的數據，各個系統有不同的實現，大致有兩種：一是存儲一個記錄 id，指向磁盤的 page 中數據的實際位置；二是直接就存儲數據本身。

B+ Tree 操作

insert

B+ 樹中插入操作大致流程如下：

• 首先從根節點開始，通過 inner node 的指針，層層往下找到對應的葉子節點 L
• 將數據存儲到葉子節點中
• 如果節點 L 中還有空閑空間，則操作完成
• 否則，分裂（split）該葉子節點

重新分布該葉子節點上的數據，以最中間的 key 為界，右邊的數據分裂到新的節點中

分裂的時候，需要將葉子節點中間的 key 推送到上層父節點

如果上層父節點又需要分裂，則重復執行上述過程

delete

delete 操作大致是和 insert 相反的，插入的時候，如果一個節點上的數據滿了，則需要分裂；而刪除時，如果一個節點中的數據少于了 M/2-1，則破壞了 B+ Tree 的定義，這時候需要將節點進行合并，稱為 merge。

大致過程如下：

• 通過 inner node 節點找到對應的葉子節點 L
• 在 L 中找到對應的數據并刪除
• 如果葉子節點中的數據大于等于 M/2-1，則完成
• 否則，需要進行 merge 合并節點

嘗試重分布，如果鄰近節點有富余，則從鄰近的節點中拿一個 key

如果鄰近節點也沒有多余的數據，則嘗試和兄弟節點合并

這里有一個網站，動態展示了 B+ 樹的插入、刪除、查找過程，能夠更好幫你理解 B+ 樹。https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html

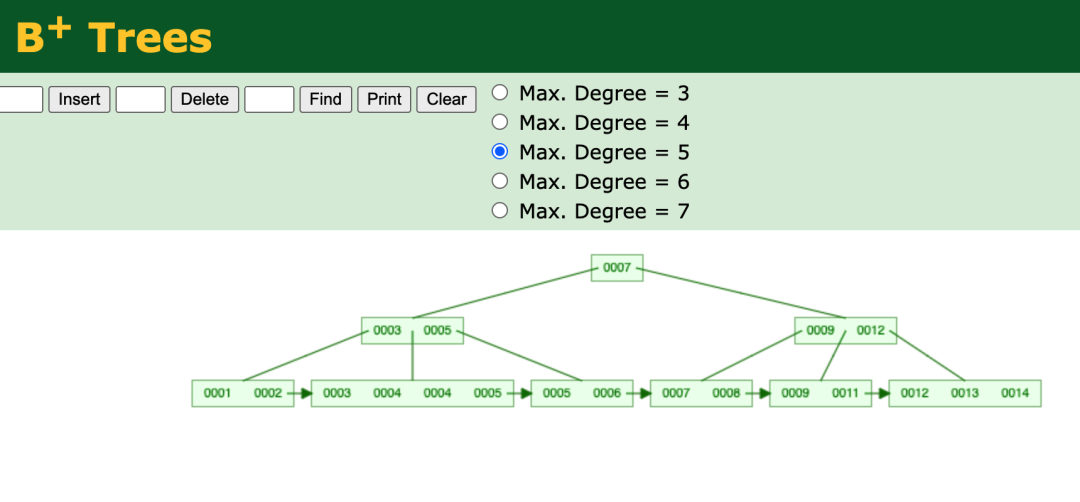
B+ Tree Design

接下來在簡要分析下關于 B+ Tree 的一些設計問題。

Node Size

對于 B+ 樹中每個節點的大小，這其實并不確定，或者說依賴于硬件環境和數據庫類型，sql 查詢類型等因素。

大致來說，存儲介質速度越慢，則一個節點的容量就越大，道理也很簡單。當在慢速的介質中，例如磁盤，我么肯定希望能夠一次性多讀取一部分數據到內存中，盡量避免多次隨機 IO。在越快速的設備上，則節點的容量越小。

可以參考內存中的 cache line 和操作系統維護的 page size。MySQL 的 B+ 樹節點大小一般是 16KB。

Merge Threshold

前面說到了刪除數據時可能會觸發 B+ 樹的 merge 節點操作，但是在實際的實現中，一些數據庫系統并不是只要滿足條件就會馬上執行，而是累積到一段時間之后，再進行 merge。

因為 merge 是一個很“昂貴”的操作，涉及到磁盤上的數據調整分布，一些系統中會有一些后臺進程，定期去觸發這個操作。

Variable-Length Keys

前面提到的 B+ Tree 中存儲的都是固定 size 的 key，但是實際環境中，我們的 key 或者 value 都有可能是不定長的。針對不定長的 key，一般有這幾種解決辦法：

1.節點中不存儲實際的 key，而是存儲指向實際 tuple 屬性的指針，這樣的話雖然能夠固定大小，但是指針并沒有 key 本身具有的特征，范圍掃描低效，實際使用并不多。

2.節點的 size 也不固定，來適配不同長度的 key

• 這種方式需要更加精細化的內存管理，并且在 buffer pool 中也需要適配（buffer pool 的 size 通常是固定的），所以實際使用也不多。

3.對齊，總是將 key 對齊為其類型的大小，而不管 key 的 size 有多大。這種方式缺點也顯而易見，就是可能會浪費一定的空間。

4.使用類似 slot page 的組織方式，將 key 存在一個有序的集合中，并且指向其實際的數據。

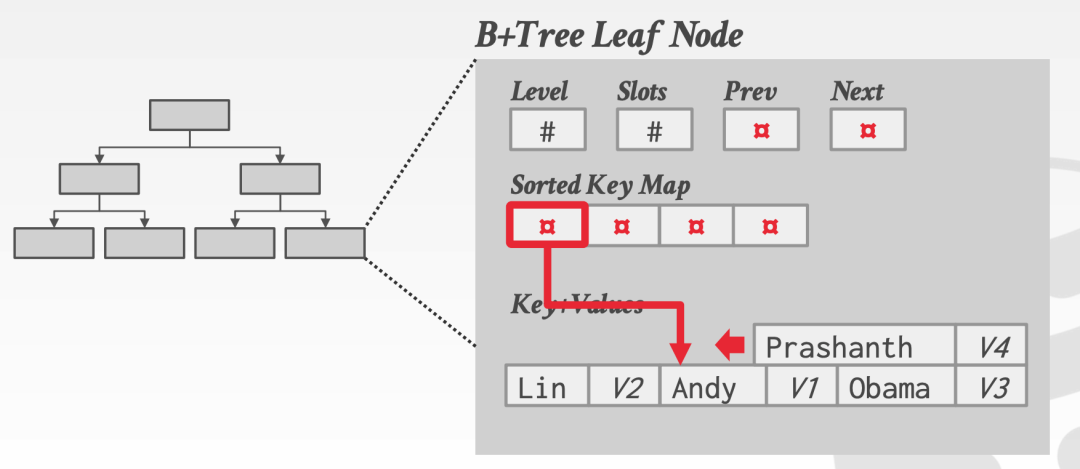
Non-Unique Index

數據庫中的索引，有時候可以存在重復的數據，除了唯一索引外。因此，在 B+ Tree 存儲數據的時候，需要對重復的 key 進行處理。

Duplicate Keys

存儲重復 key 很好理解，就是我們可以把重復的 key 也當做是一個單獨的 key 進行存儲即可。

Va

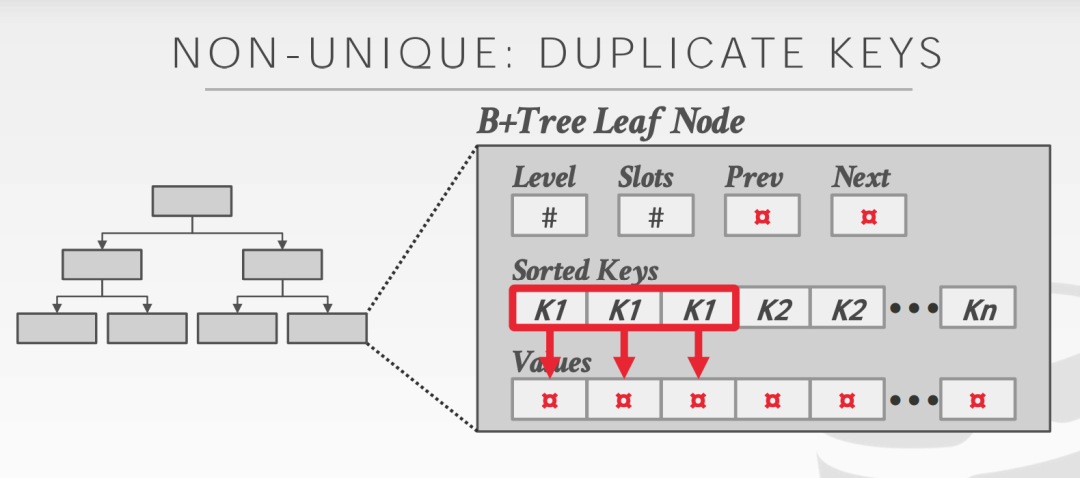
lue List

value list 就是對重復 key 的 value 維護了一個鏈表，將其串聯起來。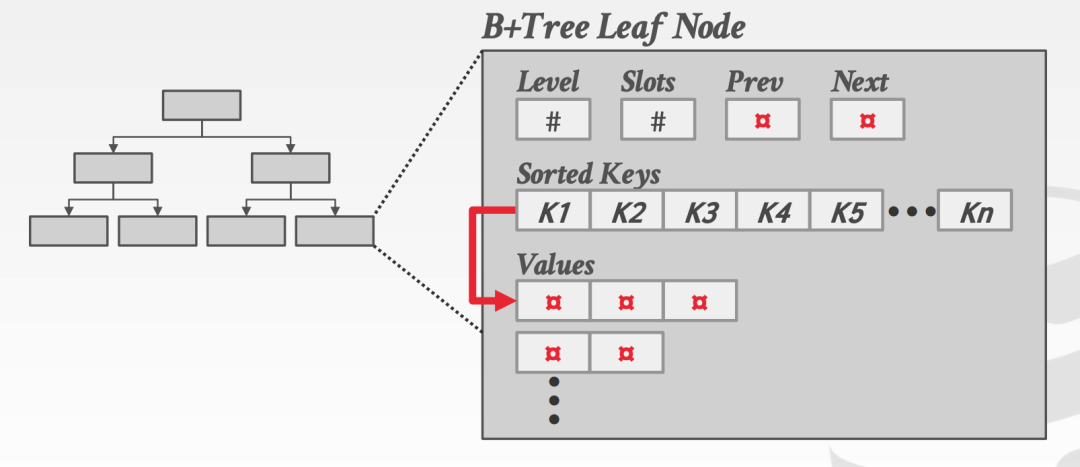

B+ Tree Optimizations

最后再來看下關于 B+ 樹在設計時的一些優化方案。

Prefix Compression

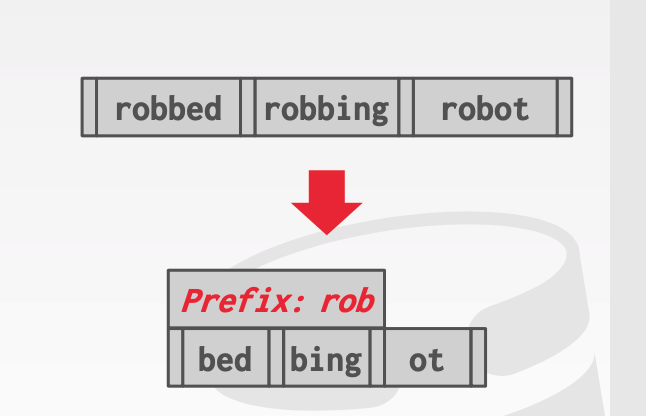
因為 B+ 樹底層葉子節點的數據是有序排列的，因此存儲在同一個葉子節點的數據，有很大可能是具有相同的特征的，例如可能是類似的，擁有相同的前綴。

所以，針對那些有相同前綴的數據，可以只存儲一份前綴數據，而不用每個 key 都單獨存儲一份。

Suffix Truncation

前面提到過 B+ 樹中 inner node 只存儲了 key 和索引信息，并不存儲數據，只是做為一個輔助查找的索引節點。因此 inner node 中的 key 并不用是完整的 key，只要能夠起到區分查找的作用就可以了。

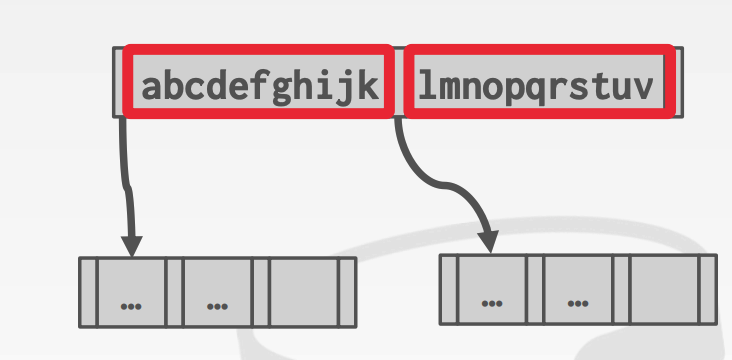
例如上面的例子，由于這兩個 key 所有字符都不一致，因此并不需要存儲完整的 key，只需要存儲能夠幫助查找到下一級節點的信息就可以了。

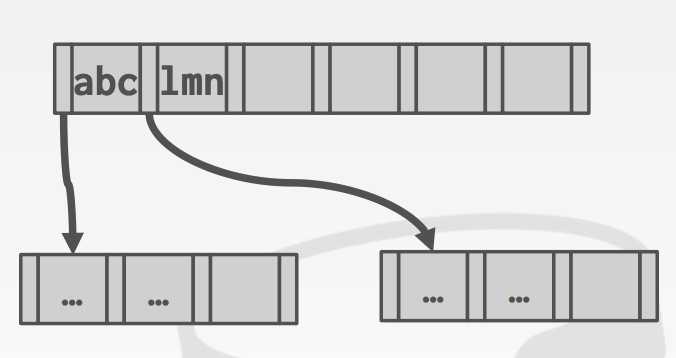
Bulk Insert

最好的構建 B+ 樹的方式，是將一組有序的數據從下到上構建 B+ 樹的多級索引，這樣不會存在 B+ 樹的分裂或者合并，效率是最高的。

因此如果有一部分初始化數據需要插入到 B+ 樹中，可以先將其排序，然后直接構建 B+ 樹。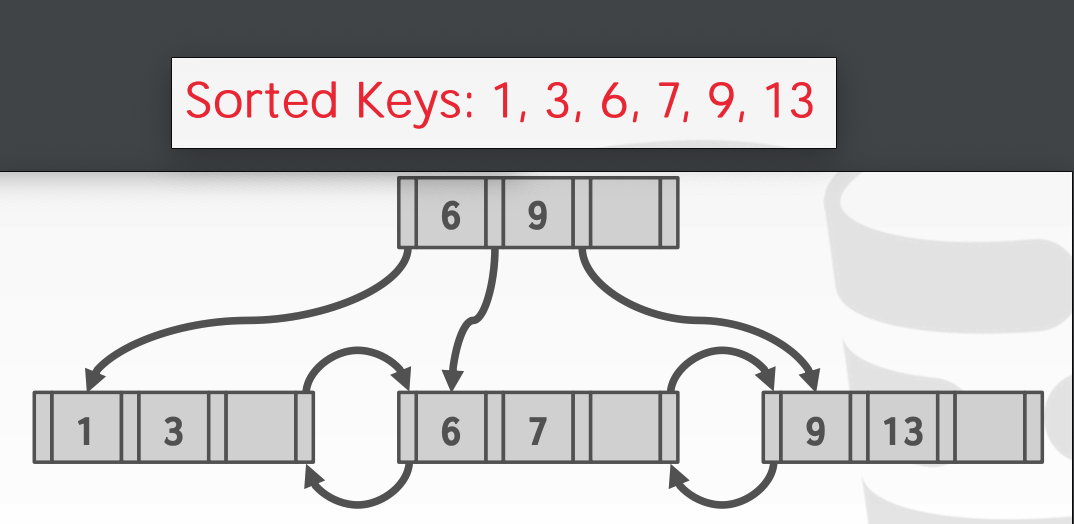

Pointer Swizzling

B+ 樹遍歷 page 的時候，每次都需要從 buffer pool 中獲取 page 的位置信息，然后 B+ 樹根據這個位置去獲取 Buffer Pool 中的 page 數據。

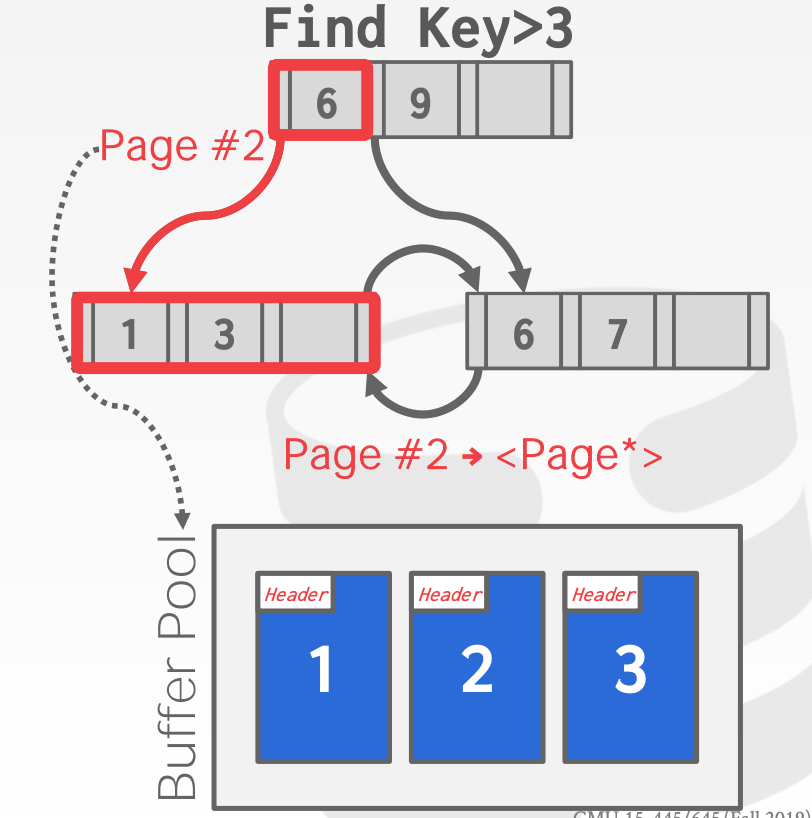
例如上圖中，需要獲取 page id 為 2 的 page，則會先從 page table 中獲取，Buffer Pool 判斷這個 page 是否在內存中，如果不在則加載這個 page 到內存，并且返回一個 page 的指針（page 的實際位置）給 B+ 樹。

如果 B+ 樹確認掃描到的 page 肯定在內存中，那么可以直接存儲 page 指針，省去了從 page table 中尋址的開銷。

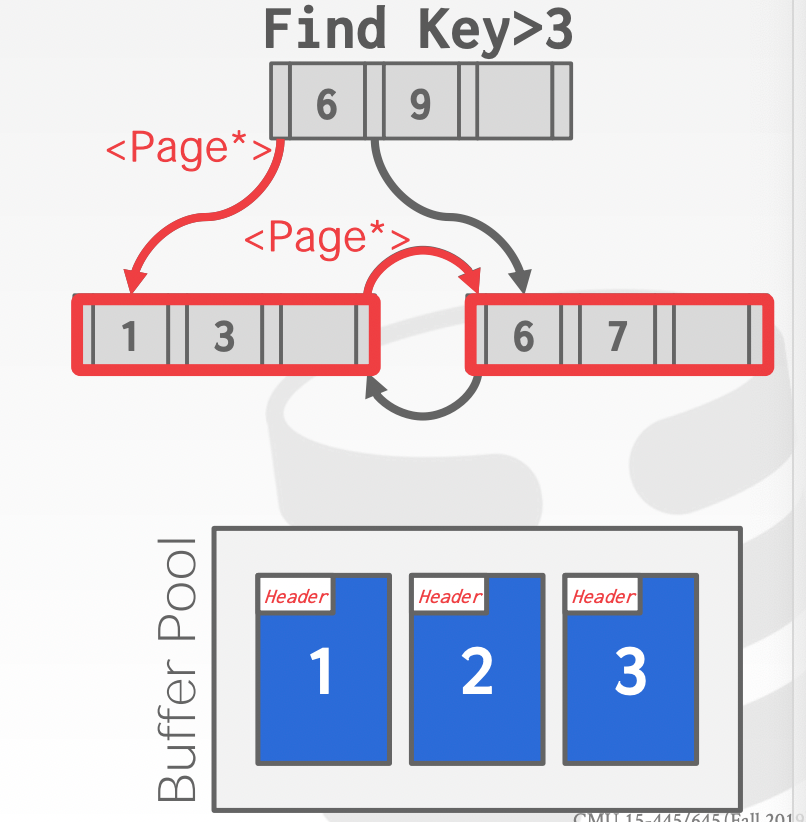
這個優化比較適用于 B+ 樹的上層節點，因為 B+ 樹上面的幾層節點容量相對較小，并且會被頻繁的訪問到，可以緩存到內存中加速 B+ 樹的查詢。

Conclusion

這一節講述了 B+ 樹的一些基本概念，相信讀者能夠對其有一個基本的理解了，在大多數情況下，B+ 樹是一個在數據庫中應用非常廣泛的結構。