一、分布式系統的需求與困境

是不是會有大佬（產品？老板？）對你所負責的分布式系統提出以下三點要求：

1. 既要：系統高可用
2. 又要：各系統數據一致且實時可見
3. 還要：系統具有集群容錯能力

這些要求看似簡單，但當你仔細思考時就會發現很讓人頭疼、無法全部實現；如果你還不理解，我們舉個例子，如防疫時期的靜態化管理：

1. 人停工企業停產（失去可用性）
2. 全城全面核酸，統一采用核酸碼平臺，實時統籌管理數據（保證數據的一致性）
3. 人被限制在小區內活動、交換物資，小區間禁止互通（分區容錯）

經歷過的人應該了解，當我們要滿足2、3時，就必須犧牲1；或許你也嘗試思考過如何破局但又困惑無解；不過無需自責，不僅是你會覺得困難，其他人也一樣，因為違背了CAP定理。

二、CAP 定理解惑

在理論計算機科學中，CAP定理（CAP theorem），又被稱作布魯爾定理（Brewer's theorem），定理討論了兩個互相矛盾的請求，到達彼此連接不通的兩個不同的分布式節點 的時候的處理方案。

CAP定理 指出對于一個分布式計算系統來說，不可能同時滿足一致性（Consistency）、可用性（Availability）、分區容錯性（Partition tolerance）。

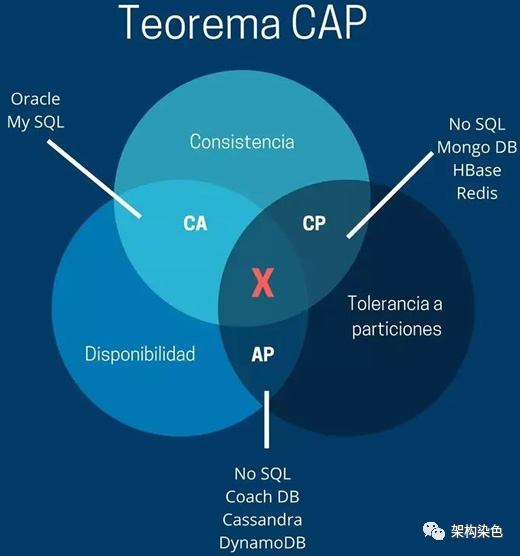
CAP定理(來自網絡).png

有這么一種說法：以實際效果而言，系統若不能在時限內完成同步，達到數據一致性；就意味著發生了分區的情況，必須就當前操作在一致性和可用性之間做出選擇。

三、一致性（Consistency）

一致性是說，所有節點訪問同一份最新的數據副本；即一致性保證了無論將數據寫入哪一個節點，其它的節點都能實時同步到這個新數據，而隨后無論從哪個節點讀到的都是最新的數據。如下圖所示：

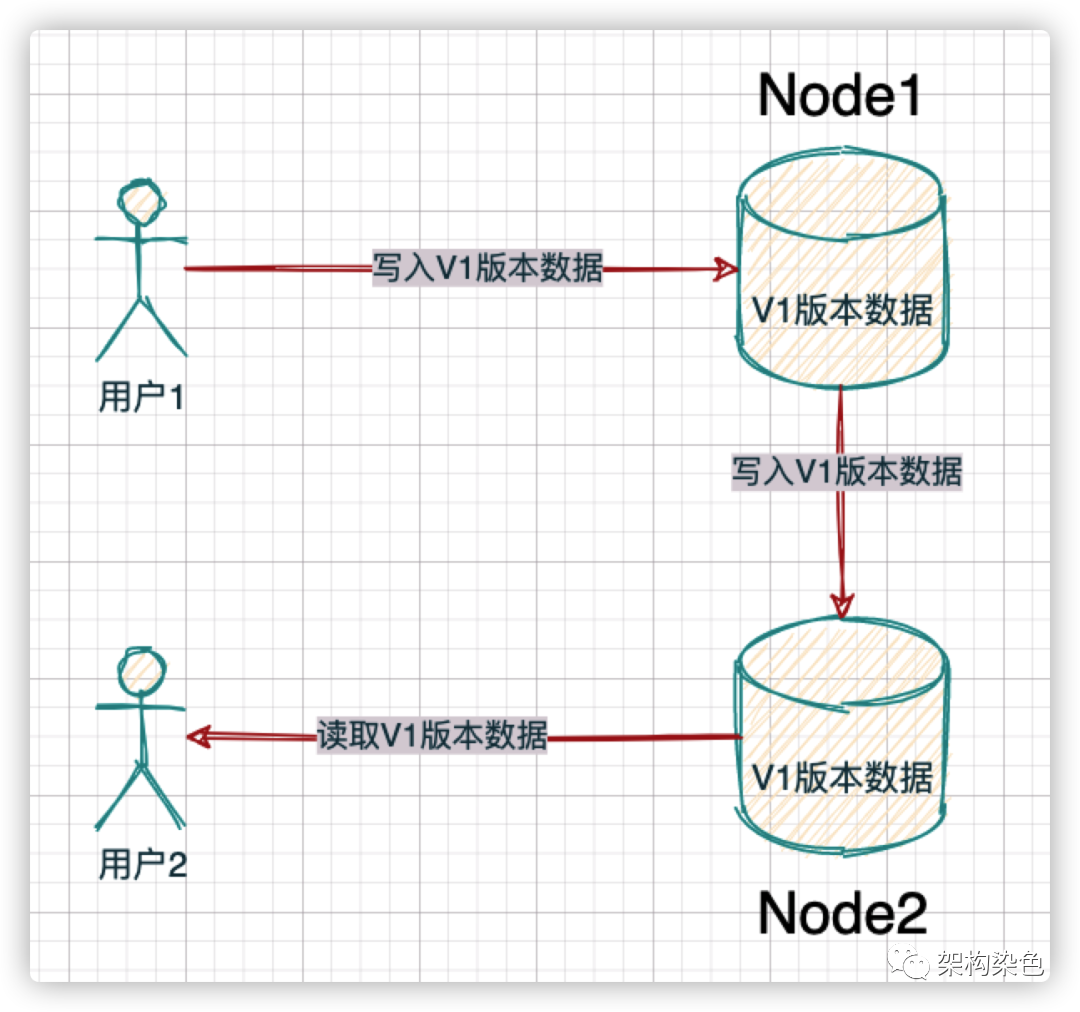
CAP定理-一致性(來自網絡).png

如果節點之間數據同步有異常，那就必須先解決掉同步的問題，掛起所有的請求，等待數據同步完成后才響應，那么會出現以下幾種情況：

• 請求在等待很久后才得到了正確結果
• 寫入數據異常
• 讀取數據異常

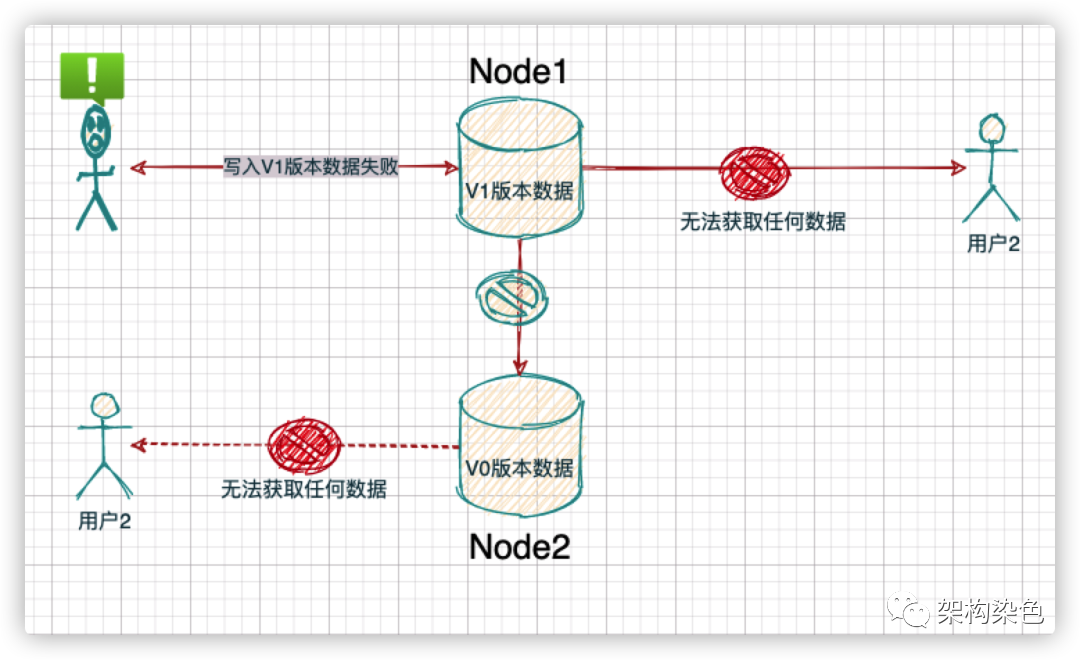
CAP定理-一致性(來自網絡)?.png

四、可用性（Availability）

可用性是說，如果有節點異常了，只要向其它無異常的節點發送請求，總能正常的收到響應數據，但數據可以不是最新的，如下圖所示：

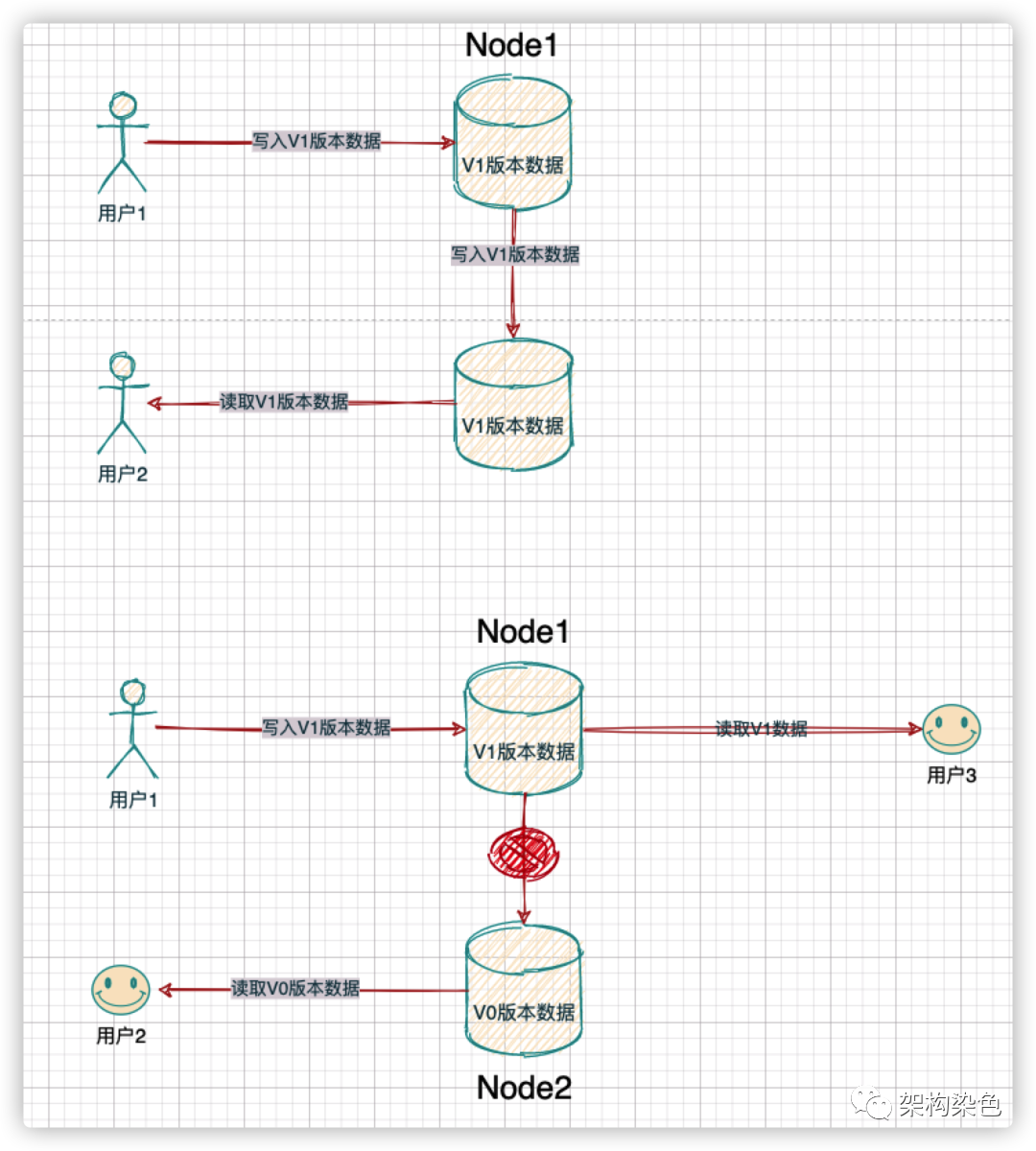
CAP定理-可用性(來自網絡)?.png

五、分區容錯性（Partition tolerance）

先說分區是什么，在分布式系統中，不同的節點分布在不同的子網絡中，若因一些網絡故障，出現了子網絡之間不通的情況，但每個子網絡內是正常的；這樣一個完整的系統就被切分成了若干個相對孤立的區域，這就是分區。

對于分布式系統來說，在遇到任何網絡故障而導致分區時，仍然能夠對外提供具有一致性或可用性的服務。也就是說會分區之間即使無法同步數據，也能對外提供服務。

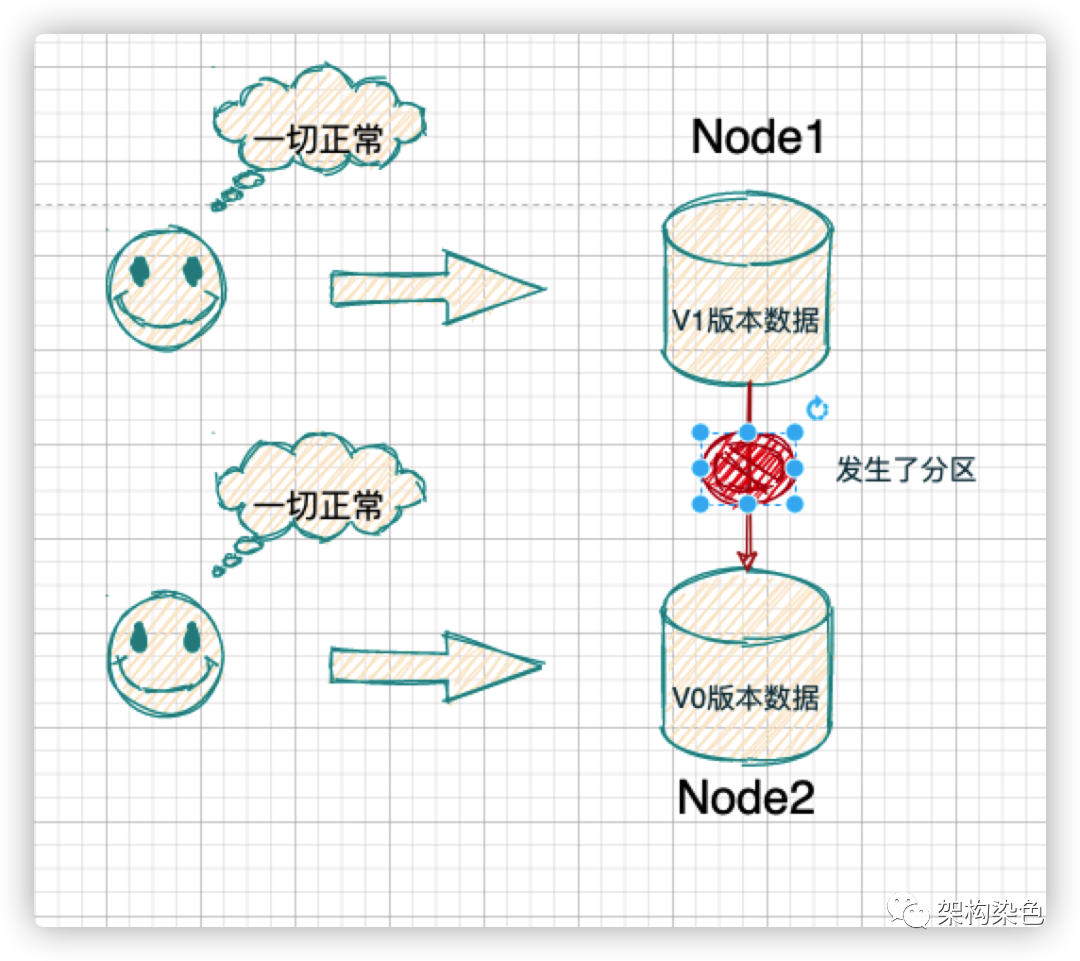
CAP定理-分區容錯性(來自網絡)

六、反推CAP定理

借用一個示例通過反證法來梳理CAP定理，如整個系統由服務節點A、B組成，節點之間通過網絡通信，當節點 A 進行更新數據操作的時候，需要同時更新節點 B 的數據。

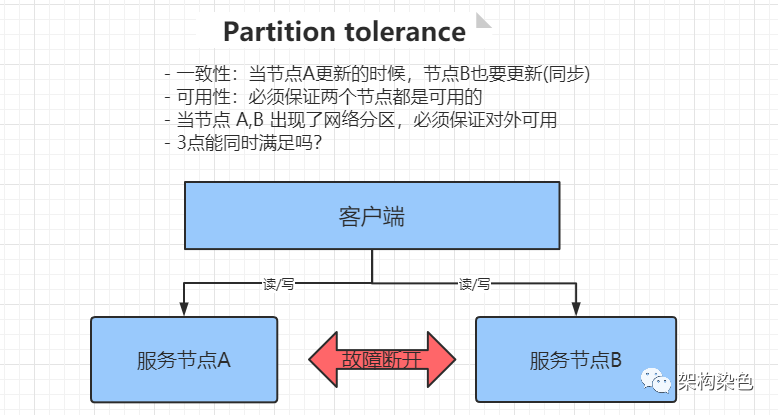
集群同步示例(來自網絡)

假設同時滿足CAP這三個特性，由于具有分區容錯能力，則可以切斷 A、B兩個節點間的通信

1. 當A、B節點通信斷開后，因無法通信，一致性就無法滿足，但A、B都還能對外提供服務，滿足可用性
2. 若要強行滿足一致性，就必須讓A、B節點不再提供服務，等A、B節點間的網絡通信故障修復后才繼續提供服務，但這就放棄了可用性。

所以總結來看：

• 若要一致性：則必須保障節點間數據同步，同步執行期間數據被鎖定、請求被掛起，會導致請求失敗或超時，破壞了可用性
• 若要可用性：則節點間數據在同步時不允許數據被鎖定、請求被掛起，這就破壞了一致性。

七、一致性的取舍

總結來說，在分布式系統中，首先必須要滿足P，因為是多節點，一定要會遇到并要容忍分區錯誤，而C或A則需要根據具體場景進行取舍。

當系統既要提供可用性，而又不能放棄一致性的情況下，通常會因場景差異而調整對一致性的要求，而差異點體現在時效性上如：

• 強一致性
  任意時刻，任意節點都能讀取到最新的數據
• 弱一致性
  可能無法在明確限定的時間內讀到最新的數據
• 最終一致性
  是一種弱一致性的特殊形式，系統保證在過了某個時間窗口后，數據將達到完全一致的狀態，而之后的讀取到的一定是新數據。

分布式業務系統實現中，多數場景中會選擇犧牲一致性來換取可用性。而所謂的犧牲其實就是不追求強一致，而選擇弱一致或最終一致。

本文轉載自微信公眾號「架構染色」，可以通過以下二維碼關注。轉載本文請聯系聯系【架構染色】公眾號作者。