徹底理解動態規劃:編輯距離
大家好,我是小風哥。
這是動態規劃主題的第三篇,本篇的題目非常經典,幾乎是面試必備,即,編輯距離問題,edit distance;
給定兩個字符串word1以及word2,返回將word1轉為word2需要的最少步驟,在每一步中你可以針對字符串word1進行以下操作:
- 新增一個字符
- 刪除一個字符
- 替換一個字符
假如word1是"horse",word2是“ros”,那么你的程序需要返回3,也就是說將word1轉為word2至少需要三個步驟:
- 將word1中的第一個字符h替換為字符r:horse -> rorse,此時word1變為rorse,word1與word2前兩個字符相等
- 將word1中的第三個字符r刪掉:rorse -> rose,此時word1變為rose,word1與word2的前三個字符相等
- 將word1中的最后一個字符刪掉:rose -> ros,此時word1與word2相等。
想一想該怎樣用動態規劃解決這個問題。
選擇與子問題
和之前的題目一樣,你首先應該找出子問題是什么,子問題與原始問題的依賴關系是什么。
找出子問題的關鍵在于每一步的選擇。
如果word1與word2的第一個字符相等,假設word1是hor、word2是hr,那么我們可以放心的排除掉兩個字符串的第一個字符,即EditDistance("hor", "hr")一定等于EditDistance("or", "r"):
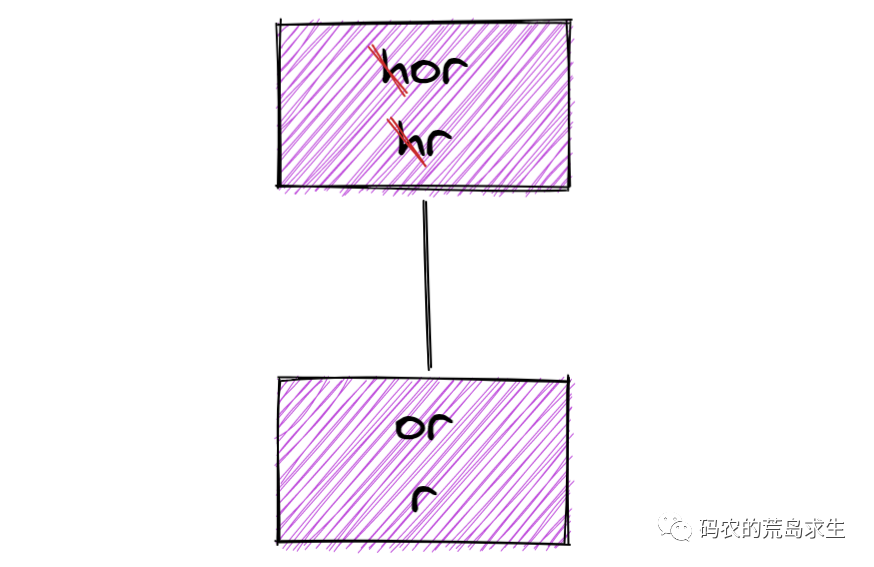
此時我們得到了一個子問題EditDistance("or", "r"),原始問題EditDistance("hor", "hr")的值等于該子問題。
真正有趣的是如果word1與word2的第一個字符不相等的情況,假設word1為“hor”,而word2為“ro”,此時根據該問題的規則針對word1的第一個字符有三種操作:
1,在word1的第一個字符前新增(Insert)一個字符r,此時word1變為rhor,由于此時word1 的第一個字符等于word2的第一個字符,可以放心的忽略掉,因此我們得到了子問題EditDistance("hor","o"),由于執行了一次新增操作,因此:
2,將word1的第一個字符刪掉(Delete),此時word1變為“or”,我們得到了一個新的子問題EditDistance("or","ro"),由于執行了一次刪除操作,因此:
3,將word1的第一個字符替換(Replace )為r,此時word1變為了“ror”,由于word1的第一個字符等于word2的第一個字符,因此可以放心的忽略掉,我們得到了一個新的子問題EditDistance("or","o"),由于執行了一次刪除操作,因此:
根據題目要求,我們需要得到最小的編輯距離,因此:
即:
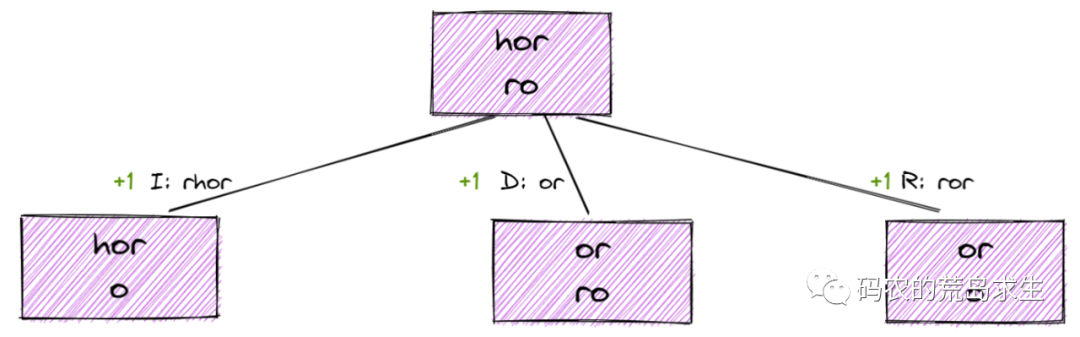
可以看到,如果word1與word2的第一個字符如果不相等的話那么我們會得到三個子問題,取這三個子問題的最小值然后加1就是原始問題的解。
現在我們找到了子問題與原始問題之間的依賴關系。
實際上,根據上述討論我們還可以進一步擴展從而得到完整的狀態空間樹。
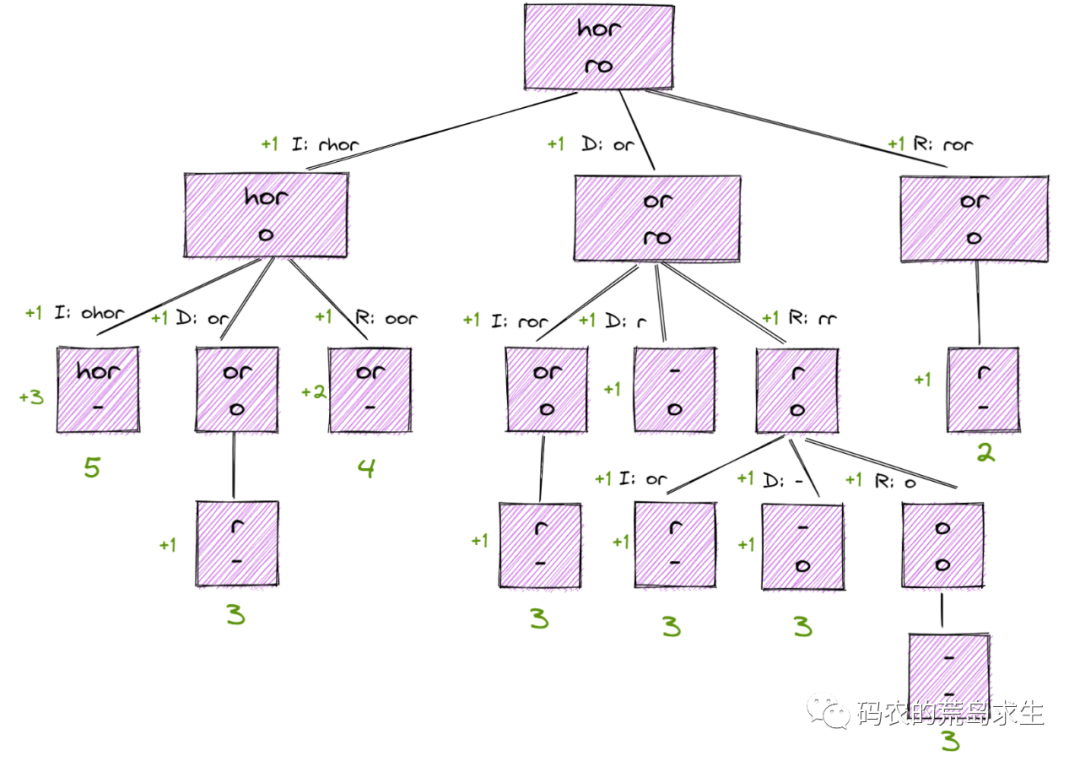
從這棵樹中可以看到最小的編輯距離是2。
現在你應該清楚的知道該怎樣我們是怎樣一步步將問題不斷的分解為更小的子問題,然后利用子問題的解來得到原始問題的解了。
自頂向下遞歸代碼
上圖中每個方框都是一個子問題,決定一個子問題的因素在于word1與word2當前處理到了哪個位置,假設對word1處理到了第i個位置,對word2處理到了第j個位置,因此我們可以對問題進行定義:
該函數表示從i到word1的末尾形成的字符串與從j從word2的末尾形成的字符串的編輯距離。
因此如果調用該函數時我們應該這樣使用:
有了該定義與上述分析,你可以輕而易舉的寫出這樣的遞歸代碼:
我們將word1與word2聲明為全局變量,這樣你可以清楚的看到決定EditDistance函數值的因素只有這兩個參數i和j,i的取值為[0, word1.length()],j的取值為[0, word2.length()],也就是說子問題的個數只有(word1.length() + 1) * (word2.length() + 1) 個,上述遞歸代碼存在大量重復計算問題,因此可以通過增加cache進行優化,這個改動就留給大家啦。
接下來我們著手將自頂向下的遞歸代碼改為自底向上的動態規劃代碼。
自底向上動態規劃代碼
由于子問題的個數只有(word1.length() + 1) * (word2.length() + 1) 個,因此可以定義一個相同大小的二維數組dp:
接下來我們要求解最小子問題,最小子問題就是上述遞歸代碼的遞歸出口:
該最小子問題的解包含在了dp數組的初始化中。
接下來的子問題是另外兩個遞歸出口:
我們可以簡單的構造出兩種情況下的所有i和j來初始化數組dp,即:
最后我們利用兩個for循環來構造出所有的i和j,從而將遞歸函數的最后一部分:
放置在for循環中,并將對遞歸函數的調用替換為對數組dp的讀寫:
最終,完整的動態規劃代碼為: