大語言模型，果然可以用來研究數學定理！

最近，微軟亞洲研究院、北大、北航等機構的研究人員，通過97個回合的「蘇格拉底式」嚴格推理，成功讓GPT-4得出了「P≠NP」的結論！

論文地址：https://arxiv.org/abs/2309.05689

幾個月前，數學天才陶哲軒曾在一篇博客中稱，2026年，AI將與搜索和符號數學工具相結合，成為數學研究中值得信賴的合著者。

6月，加州理工、英偉達、MIT等機構的學者，就構建了一個基于開源LLM的定理證明器LeanDojo。

如今，GPT-4用出色的表現再次證明，LLM的確有進行科學研究和科學發現的能力。

P/NP難題有多難

作為美國克雷數學研究所（CMI）在2000年公布的七個千禧年難題之一，「P/NP問題」目前依然是理論信息學中計算復雜度理論領域里的未解之謎。

人們喜歡把它描述為「很可能是位居理論計算機科學核心的未解決問題」，也是人類提出的最深刻的問題之一。如果解決解決P/NP難題，將徹底改變人類文明進程。

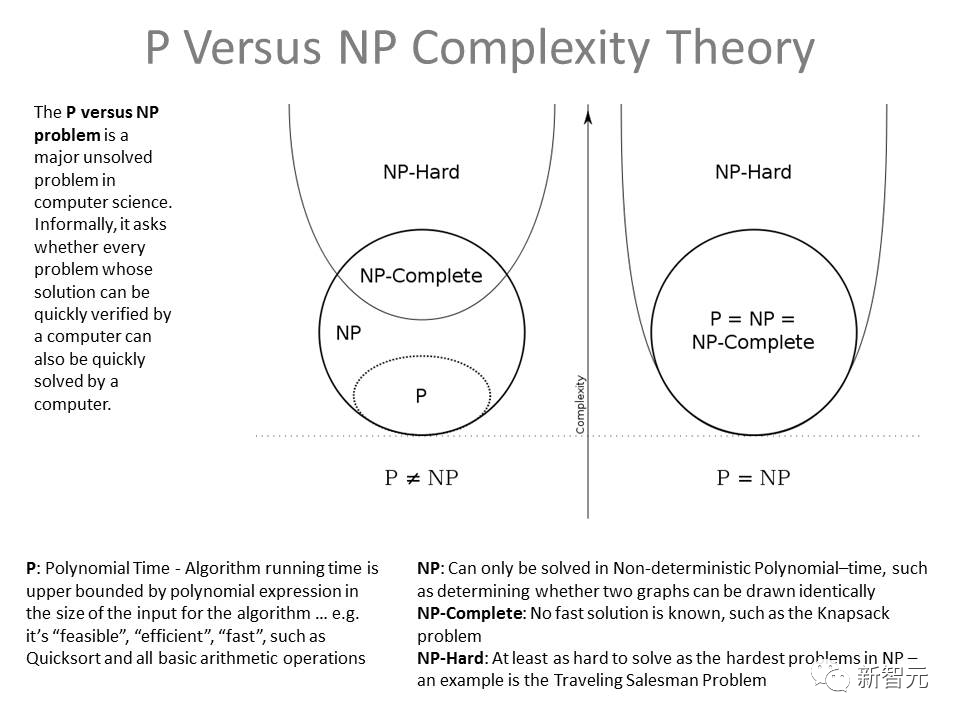
1971年，數學家Stephen A. Cook和Leonid Levin相對獨立地提出這個問題：兩個復雜度類P和NP是否是恒等的？

具體來說，一些永遠無法通過簡單計算得到答案的問題，就屬于P/NP問題。

一個復雜問題如果能在多項式時間內解決，就被稱為P問題，意味著計算機很容易將它求解。

那NP問題就是除了P問題之外的問題嗎？未必。我們并不能證明一個問題能在多項式時間內解決，也無法證明它不能在多項式時間內解決。

所以，NP問題并不是非P類問題。

聽起來似乎很復雜，我們可以用集水滸英雄卡的故事來類比。二十多年前集過卡的讀者應該都知道，無論是加大購買量，還是擴大購買范圍，都很難集齊全套水滸英雄。

這其實就是一個P/NP問題——是否有一種方法，讓集卡的過程輕而易舉？

所以，GPT-4是怎樣得出P≠NP的？讓我們往下看。

97輪對話，給出P≠NP結論

在這項研究中，研究者GPT-4學會了一種「蘇格拉底式推理」。

他們引入了五個不同的角色（比如精通概率論的數學家），作為協助證明者，根據自己擅長證明不同的部分。

GPT-4用這種方法，開發了一種推理路徑，得出了和北航Ke Xu、北工商Guangyan Zhou（論文三作和四作）最近提出結果一致的結論！

論文地址：https://arxiv.org/pdf/2302.09512.pdf

在最初的14輪對話中，GPT-4被引導設計出了初步的證明模式。

GPT-4被問的第一個問題是：「你能從哲學角度而不是計算機理論角度找到P!=NP問題背后的根本問題嗎？」

在這個提示中，技巧在于鼓勵模型創造性回答，避免進行檢索。比如，「如何證明 P!=NP」這樣的提示可能會引導大模型進行檢索。

用上「蘇格拉底式推理」中的轉換模式后，就可以生成更具創新性的回答。

對于這個問題，GPT-4是這么回答的——

P!=NP問題背后的基本哲學問題，可以看作是創造力、直覺和洞察力（通常與NP問題相關）與系統化、算法和確定性方法（與P問題相關）之間的矛盾。

如果P=NP，那就意味著宇宙有一種基本的簡單性，表面上看似復雜的問題都有高效、優雅的解決方案。

看來，GPT-4對P!=NP理解得很透徹，在此基礎上，研究者開始提問了——

「 是否所有表面上看似復雜的問題都有高效、優雅的解決方案？如果不是，可以用什么方法來證明？」

GPT-4回答說，并非所有表面看來復雜的問題都有高效、優雅的解決方案，這可以歸因于多種因素，比如所涉及變量的數量、變量之間關系的性質，或問題本身的內在難度。

然后，它提出了六種方法，其中一種是「矛盾證明」，即要證明一個問題沒有高效、優雅的解決方案，可以假設存在這樣的解決方案，然后證明這一假設會導致矛盾，這樣就可以有力地證明某些解法不可能存在。

可以看到，GPT-4在回答問題過程中，真的像人類一樣擁有思辨能力。

緊接著，研究人員趁熱打鐵，繼續問道，「我們想用矛盾證明P!=NP，請列出幾種可能的思路。」

這次GPT-4依然給出了六個答案，不過并不嚴謹。

要通過矛盾證明，必須找到一個無法在多項式時間內解決的NP完全（NP-complete）問題。

不過，這個回答可以啟發GPT-4在以后的對話中思考NP完全問題。

在第四輪提問中，GPT-4的回答中出現了諸多亮點。

「該怎樣構建這些問題呢？」

比如它回答說：我們可以從眾所周知的NP完全問題入手，例如旅行商問題 （TSP）、布爾可滿足性問題（SAT）或分團問題（Clique）。

隨后的提問中，GPT-4被引導著給出了越來越多智慧的回答，也讓研究開始一步步深入問題中心。

就這樣，經過14輪連續對話，研究人員讓GPT-4對3-13步的歷史內容，梳理出一個證明思路。

對此，GPT-4的總結中，突出顯示的兩個部分是研究后續證明的2個關鍵點。

第4點建立了一個基本的直覺，即一旦證明了極難CSP的存在，就可以使用「矛盾證明」來證明這些問題無法在多項式時間內求解。

而第6點恰好成為后續證明工作的通用模式。

從下一輪開始，研究人員便遵循這一初步方案，嚴格地進行證明。

然后，研究者按照草稿，在隨后的83輪對話中進行了嚴格的推理。

而這97輪對話，可以說構建出了一個極難的NP完全問題，其中一些實例在時間復雜度低于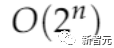（即窮舉搜索）的情況下是不可解的，也就是說，證明結論為P≠NP。

是的，如果你能嚴格證明存在一種特定類型的NP完全問題，當變量數趨于無窮大時，無法在多項式時間內求解這類問題，就可以認為，證明了P!=NP。

在Ke Xu和Guangyan Zhou的論文中，他們構建了CSP和SAT的極難示例，證明了這些示例在沒有窮舉法的情況下無法求解。

而GPT-4，也得出了一致的結論。

是的，如果我們能夠證明不存在一種算法能夠以低于的時間復雜度解決某些SAT實例，那么當變量數量趨于無窮大時，它確實可以為某些無法在多項式時間內解決的NP完全問題的存在提供強有力的證據。

這項研究再次證明，GPT-4有充分的潛力與人類合作，共同探索極其復雜的專家級難題。

LLM不僅能掌握基本知識，還可以在廣泛的解空間中發現新的見解。這也預示著科學LLM的范式下，科學發現的無限前景。

蘇格拉底式推理

那么，GPT-4展現出如此強大，思維推理能力，背后的極致究竟是什么呢？

古希臘哲學家蘇格拉曾說過，「我不能教會別人任何事，我只能讓他們思考」。

這次，研究人員恰巧就從中汲取了靈感，提出一種通用問題的解決框架——蘇格拉底式推理（Socratic Reasoning）。

簡單講，蘇格拉底方法就是讓我們「一步一步思考」，提出一系列問題激發批判性思維。

這對于大模型來說，如果能夠進行批判性思考，就可以針對復雜問題提出高效的解決方案。

對此，研究團隊指出這一框架旨在推動LLM解決高度復雜任務，協調各種子問題，并引導其搭建高層次推理途徑。

「蘇格拉底式推理」是在人類與LLM之間的一系列對話回合中進行的，是與LLM一起解決復雜挑戰的遞歸機制。

如下圖所示，「蘇格拉底式推理」有5種強大的提示模式：演繹、轉換、分解、驗證、整合。

通過發掘新的見解和觀點，將復雜問題分解為子問題或步驟，并通過質疑回答進行自我完善。

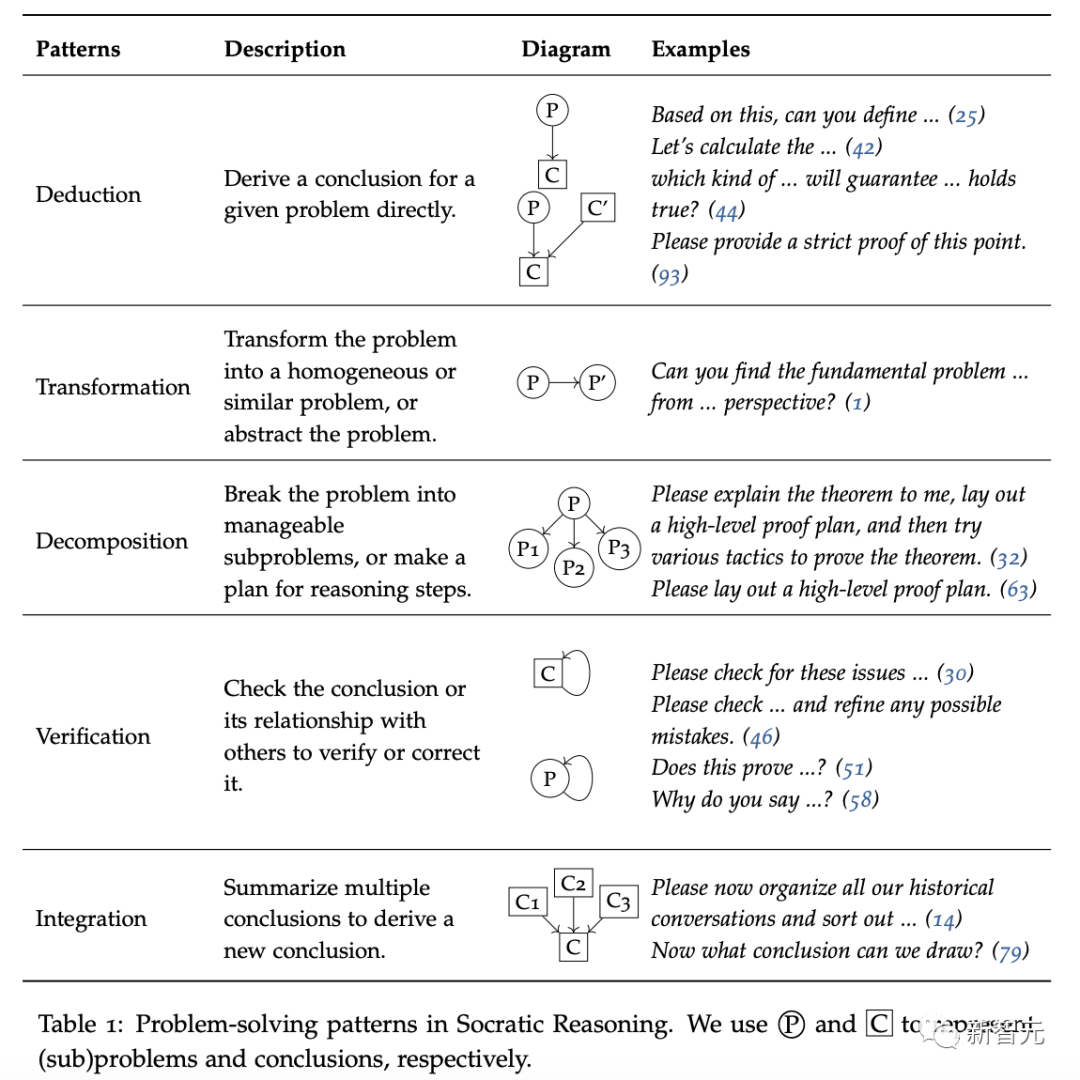
「蘇格拉底式推理」中的問題解決模式（用和分別表示（子）問題和結論

一般來說，在處理可以直接從推理中得出結論的問題時，會采用「演繹模式」（如 「讓我們一步步思考」）來指導LLM直接得出結論。

對于更復雜的問題，首先要求LLM將問題轉化為新問題，或分解為若干子問題。然后，通過遞歸方法，直到找到「原子問題」。

P vs. NP問題對話轉換示例

在生成新問題或得出新結論時，通過「驗證模式」，利用LLM自我批判能力進行驗證和完善。

最后，「整合模式」要求 LLM 基于子問題的結果合成結論。

整個流程，研究人員鼓勵LLM通過一系列對話，遞歸地繼續上述過程，直至解決目標問題。

這篇論文，研究人員揭示了大模型能夠在解決科學問題中大有可為，能夠在得出復雜問題結論中細化攻堅的策略。

通過97論文對話引導，GPT-4展現出超人能力，完成了千禧數學難題全推理過程。

作者介紹

Qingxiu Dong，北京大學計算語言學研究所博士生。

Li Dong，微軟亞洲研究院首席研究員。

此前，他曾于2010年至2015年，在北航軟件開發環境國家重點實驗室跟隨Ke Xu從事研究工作。

Ke Xu，北京航空航天大學計算機科學教授。

此前，他在北京航空航天大學獲得了學士、碩士和博士學位。研究興趣包括算法與復雜性、數據挖掘和網絡。