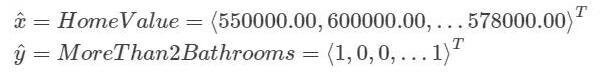過去十年來，深度學習領域發展迅速，其一大主要推動力便是并行化。通過 GPU 和 TPU 等專用硬件加速器，深度學習中廣泛使用的矩陣乘法可以得到快速評估，從而可以快速執行試錯型的深度學習研究。

盡管并行化已經在深度學習研究中得到了廣泛的使用，但循環神經網絡（RNN）和神經常微分方程（NeuralODE）等序列模型卻尚未能完全受益于此，因為它們本身需要對序列長度執行序列式的評估。

序列評估已經變成了訓練序列式深度學習模型的瓶頸。這一瓶頸可能會使人們關注的研究方向偏離序列模型。

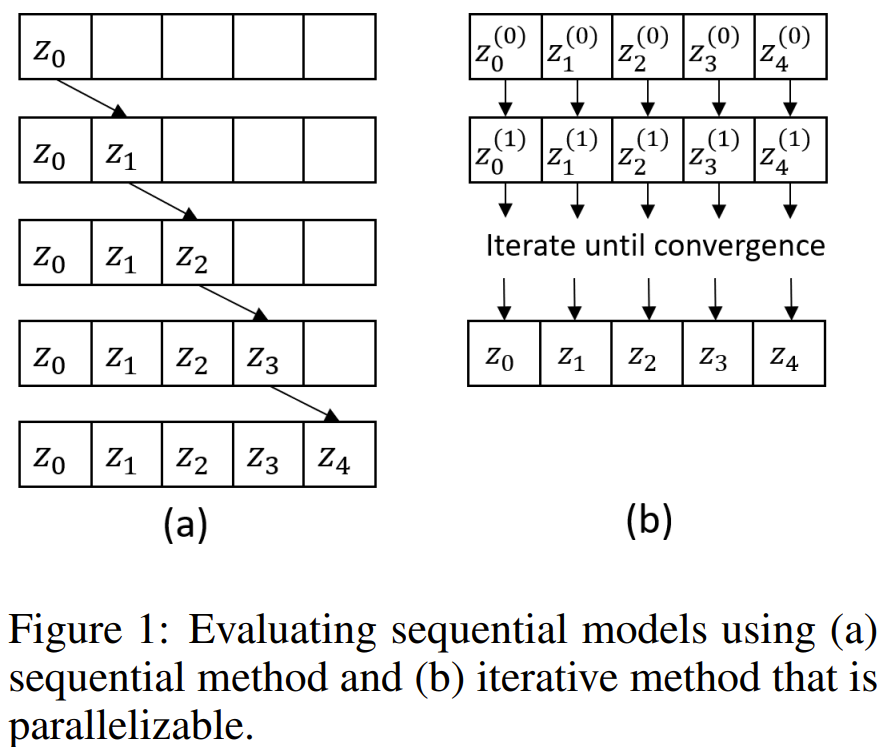
舉個例子，注意力機制和 transformer 在近些年中超過 RNN 成為了語言建模的主導技術，部分原因就是它們能以并行的方式訓練。連續歸一化流（CNF）過去常使用的模型是 NeuralODE，現在卻轉向了訓練過程不涉及到模擬 ODE 的新方向。

近期有一些嘗試復興序列 RNN 的研究工作，但它們的重心都是線性循環層 —— 可使用前綴掃描（prefix scan）來進行并行化地評估，非線性循環層在其序列長度上依然無法并行化。

近日，英國 Machine Discovery 公司和牛津大學的一篇論文提出了一種新算法，可將 RNN 和 NeuralODE 等非線性序列模型的評估和訓練工作并行化，并且他們宣稱這一算法還不會在「合理的數值精度」內改變模型的輸出。

論文地址：https://arxiv.org/pdf/2309.12252.pdf

那么他們是怎么做到這一點的呢？

據介紹，他們引入了一種用于求解非線性微分方程的通用框架，其做法是將這些方程重新表述為二次收斂的定點迭代問題，這相當于牛頓求根法。定點迭代涉及到可并行運算和一個可并行地評估的逆線性算子，即使是對于 RNN 和 ODE 這樣的序列模型也可以。

由于是二次收斂，所以定點迭代的數量可以相當小，尤其是當初始起點接近收斂的解時。在訓練序列模型方面，這是一個相當吸引人的功能。由于模型參數通常是漸進式更新的，所以之前訓練步驟的結果可以被用作初始起點。

最重要的是，研究者表示，新提出的算法無需序列模型具備某種特定結構，這樣一來，用戶不必改變模型的架構也能收獲并行化的好處。 

DEER 框架：將非線性微分方程視為定點迭代

DEER 框架具有二次收斂性，并且與牛頓法存在關聯。這一框架可以應用于一維微分方程（即 ODE），也可用于更高維的微分方程（即偏微分方程 / PDE）。該框架還可以應用于離散差分方程以達到相同的收斂速度，這一特性可以應用于 RNN。

使用該框架，用戶可以設計一種用于評估 RNN 和 ODE 的并行算法，并且不會對結果產生明顯的影響。

DEER 框架

令我們感興趣的輸出信號為 y (r)，其由 n 個在 d 維空間的信號構成，其坐標表示為 r。輸出信號 y (r) 可能依賴于輸入信號 x (r)，其關系是某個非線性的延遲微分方程（DE）：

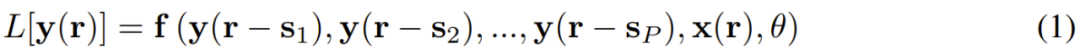
其中 L [?] 是 DE 的線性算子，f 是非線性函數，其依賴于 P 個不同位置的 y 值、外部輸入 x 和參數 θ 的。這是一個通用形式，足以表示各種連續微分方程，比如 ODE（當 L [?] = d/dt 且 r = t）、偏微分方程（PDE）、甚至用于 RNN 的離散差分方程。

現在，在左側和右側添加一項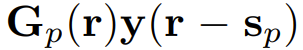，其中 Gp (r) 是一個依賴于位置 r 的 n×n 矩陣。G_p 的值會在后面決定。現在 1 式就變成了：

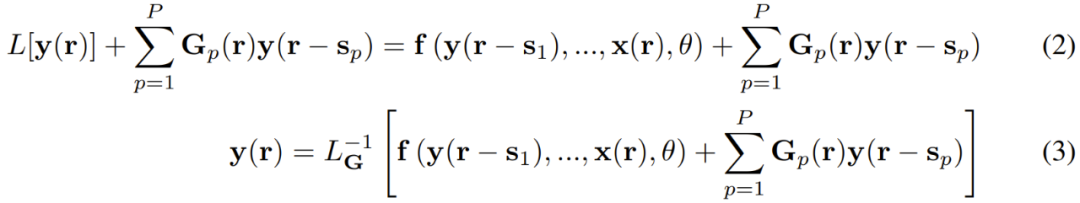
2 式的左側是一個關于 y 的線性方程，在大多數情況下，其求解難度都低于求解非線性方程。在 3 式中，研究者引入了一個新符號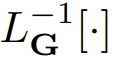，用以表示在給定邊界條件下求解 2 式左側的線性算子的線性算子。

3 式可被看作是一個定點迭代問題，即給定一個初始猜測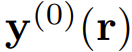，可以迭代地計算等式右側，直到其收斂。為了分析這種接近真實解的收斂性，這里將第 i 輪迭代時的 y 值記為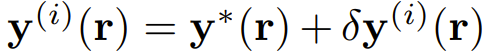，其中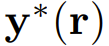是滿足 3 式的真實解。將 y^(i) 代入 3 式可以得到 y^(i+1)，然后泰勒展開至一階，得：

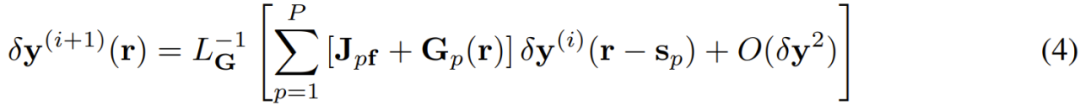
其中 J_pf 是 f 在其第 p 個參數上的雅可比矩陣。根據上式，通過選擇

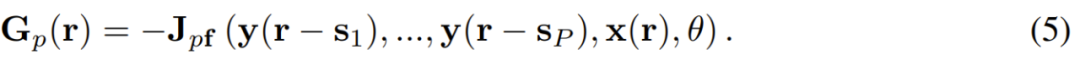
可讓 δy^(i+1) 的一階項為 0。

這表明，根據上式選擇矩陣 G_p，能以最快的速度收斂到解附近。這還表明，3 式和 5 式中的迭代相當于在巴拿赫空間（Banach space）中實現牛頓法，因此能提供二次收斂性。

3 式中的迭代過程涉及到評估函數 f、其雅可比矩陣和矩陣乘法，這些運算可以使用現代加速器（如 GPU 和 TPU）來并行化處理。如果能以并行方式求解線性方程，那么整個迭代過程都可利用并行計算。在深度學習背景中，將非線性微分方程視為定點迭代問題來求解還有另一個優勢，即可以將前一步驟的解（如果能放入內存）用作下一訓練步驟的起始猜測。如果起始猜測更好，則能減少尋找非線性微分方程的解所需的迭代步驟。

實際實現

為了將 3 式的 DEER 框架用于具體問題，需要遵循一些步驟。

第一步是將問題改寫成 1 式，定義變量 y、線性算子 L [?] 和非線性函數 f (?)。

第二步是實現研究者所說的位移器函數（shifter function）。這個位移器函數是以 y (r) 的整體離散值為輸入，返回經過位移的 y 值的列表，即 y (r ? s_p)，其中 p = {1, ..., P}。這個位移器函數可能需要一些附加信息，比如起始或邊界條件。這個位移器函數的輸出將會是非線性函數的輸入。

下一步（通常也是最難的一步）是根據矩陣列表 G_p 和在某些點離散的向量值 h 實現逆算子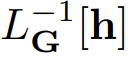。這個逆算子可能也需要有關邊界條件的信息。

只要能提供算法 1 中的需求，就可以將 DEER 框架應用于任意微分或差分方程。

并行化常微分方程（ODE）

ODE 的形式通常是 dy/dt = f (y (t), x (t), θ)，其中初始條件 y (0) 是已給定的。上面的 ODE 形式如果用 1 式表示，則有 r = t、L = d/dt、P = 1 和 s_1 = 0。這意味著 ODE 中的算子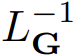相當于在給定初始條件 y (0) 時求解下面的線性方程。

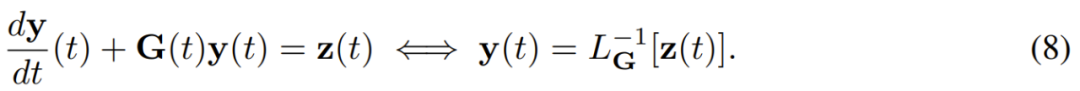
假設 G (t) 和 z (t) 是 t = t_i 和 t = t_{i+1} 之間的常量，分別為 G_i 和 z_i，則可以將 y_{i+1}=y_(t_i+1) 和 y_i = y (t_i) 之間的關系寫成：

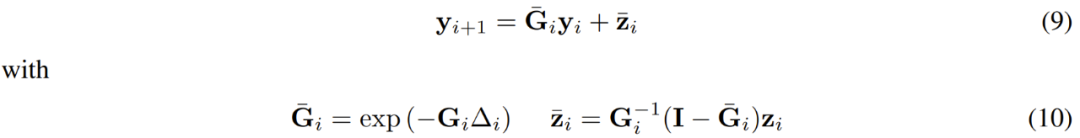
其中 ?_i = t_{i+1} ? t_i，I 是單位矩陣，exp (?) 是矩陣指數。9 式可以使用并行前綴掃貓算法進行評估。具體來說，首先可以為每個離散時間點 t_i 定義一對變量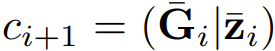，初始值 c_0=(I|y_0) 以及一個關聯算子

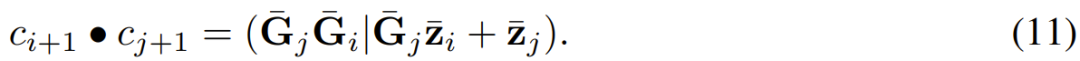
給定上面的初始值 c_0 和關聯算子，可以并行方式運行關聯掃描以獲取上述算子的累積值。解 y_i 可從這個并行掃描算子的結果的第二個元素獲取。

并行化 RNN

循環神經網絡（RNN）可以看作是一種離散版的 ODE。令索引 x 處的輸入信號為 x_i，前一狀態為 y_{i-1}，則當前狀態可以寫成 y_i = f (y_{i-1}, x_i , θ)。

這個形式可以捕獲常見的 RNN 單元，比如 LSTM 和 GRU。而如果用 1 式來寫這個形式，則有 r = i、L [y] = y、P = 1 和 s_1 = 1。這意味著給定起始狀態 y_0，可以通過求解下式來計算逆線性算子：

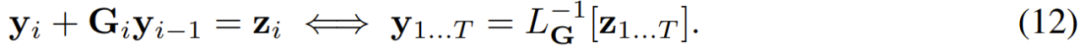
求解上式就相當于求解前一小節的 9 式。這意味著也可以使用并行前綴掃描和 11 式中定義的關聯算子來將其并行化。

實驗

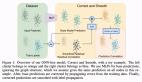
圖 2 給出了新提出的方法在 V100 GPU 上所實現的速度提升。

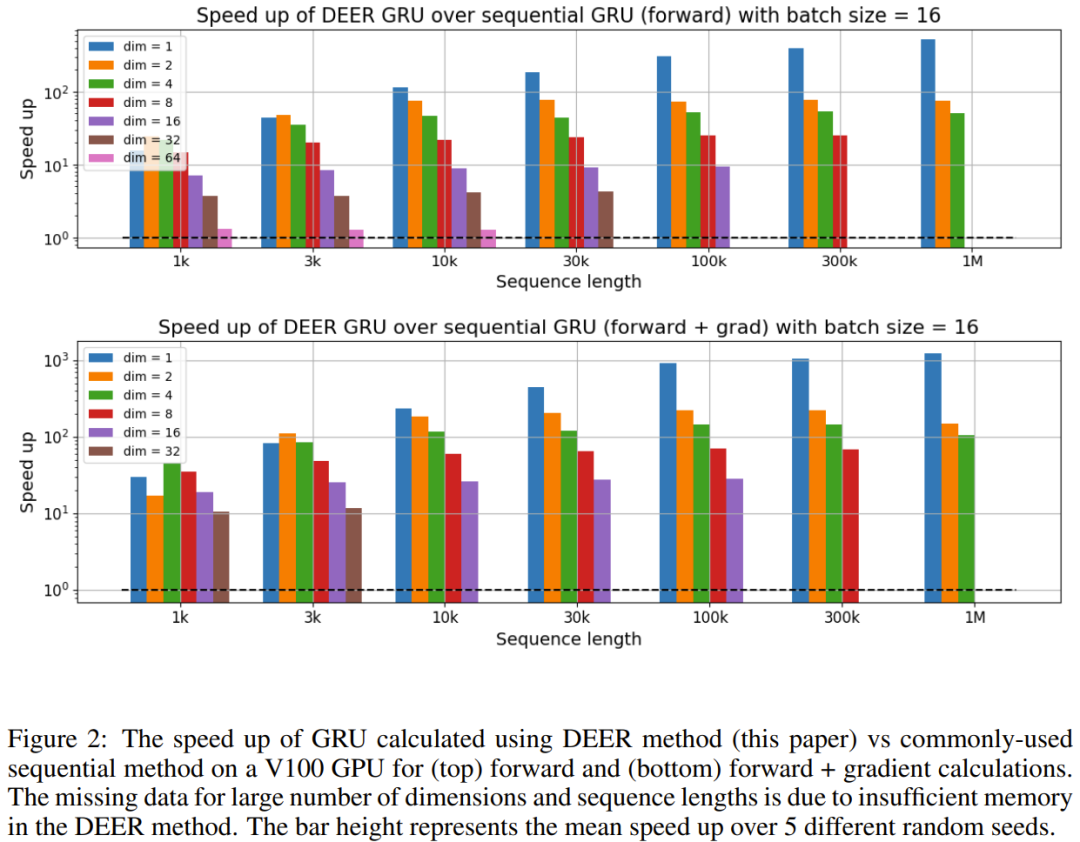
這張圖表明，當維度小、序列長度長時，取得的速度提升最大。但是，隨著維度增多，速度提升會下降。對前向 + 梯度計算的提速甚至超過僅前向計算的提速。

圖 3 比較了使用序列方法和 DEER 方法評估的 GRU 的輸出。

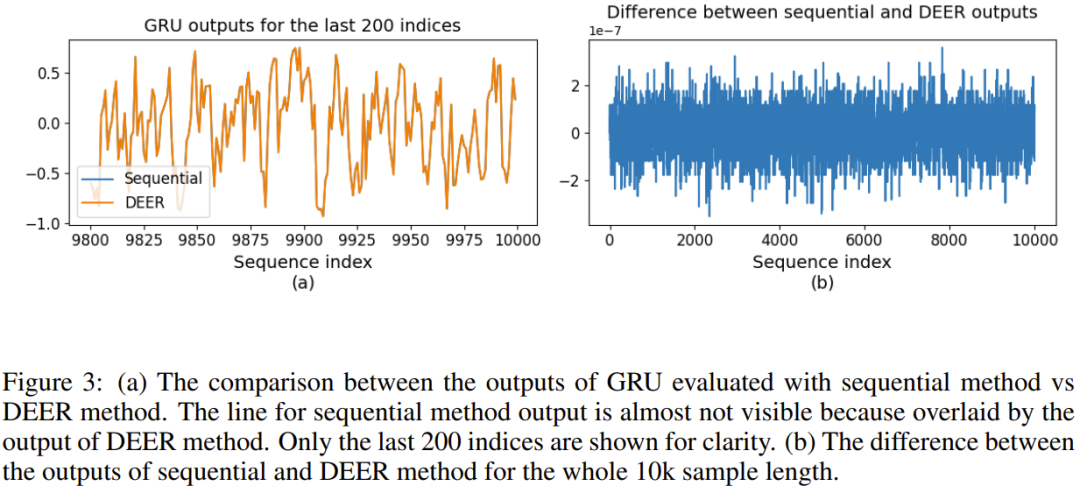
從圖 3 可以看出，使用 DEER 方法評估的 GRU 的輸出幾乎與使用序列方法獲得的輸出一樣。圖 3 (b) 中的小誤差源于單精度浮點的數值精度限制。

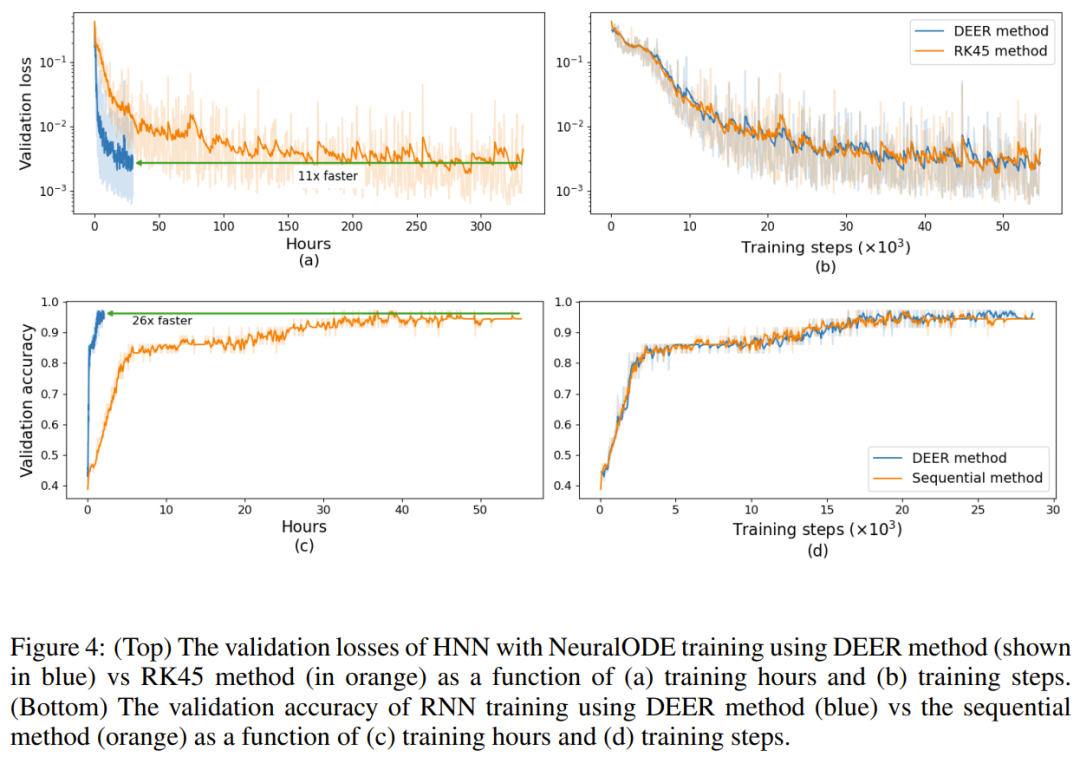
圖 4 (a, b). 給出了使用 DEER 方法和 RK45 方法時訓練期間的損失變化情況。從圖中可以看到，相比于使用普通的 ODE 求解器，當使用新提出的 DEER 方法時，訓練速度可以提升 11 倍，并且這兩種方法的驗證損失差別不大。

圖 4 (c, d) 比較了使用 DEER 方法和常用的序列方法時，GRU 網絡訓練期間的驗證準確度。從圖中可以看到，使用 DEER 方法時的驗證準確度圖表與使用序列方法時的很相近。