數據科學在騰訊內容生態中的應用

一、數據是什么樣子的?
1、正態分布
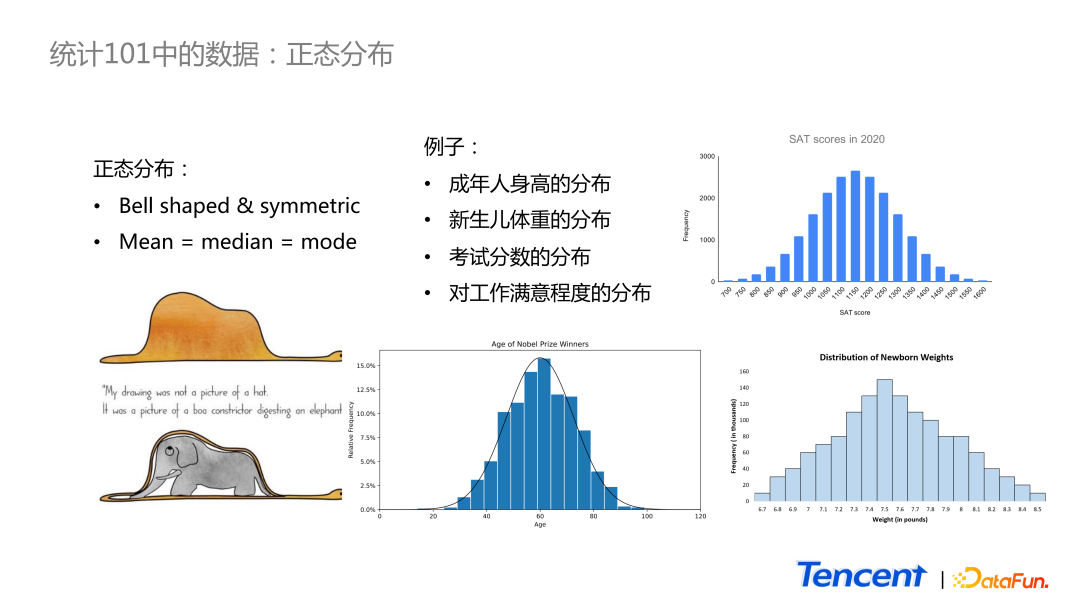
統計學教材中首個連續分布就是正態分布。如圖中所示,正態分布看上去是一個對稱的鐘型分布圖形。在正態分布里,均值、中位數和眾數一般是相等的。教材中有兩個經典的正態分布的例子:考試分數的分布和新生兒體重的分布。還比如諾貝爾獎得主年齡的分布,也是正態分布。
雖然正態分布很經典,應用很廣泛,但是從個人角度而言,這個分布在日常生活中感知并不強烈。用成年人的身高來舉例,雖然我們知道身邊很多朋友的身高,但是在腦海里很難形成一個很鮮明的分布的概念。
而在日常生活中,讓我感知比較強烈的是另外一個分布——Power Law。
2、The Power Law
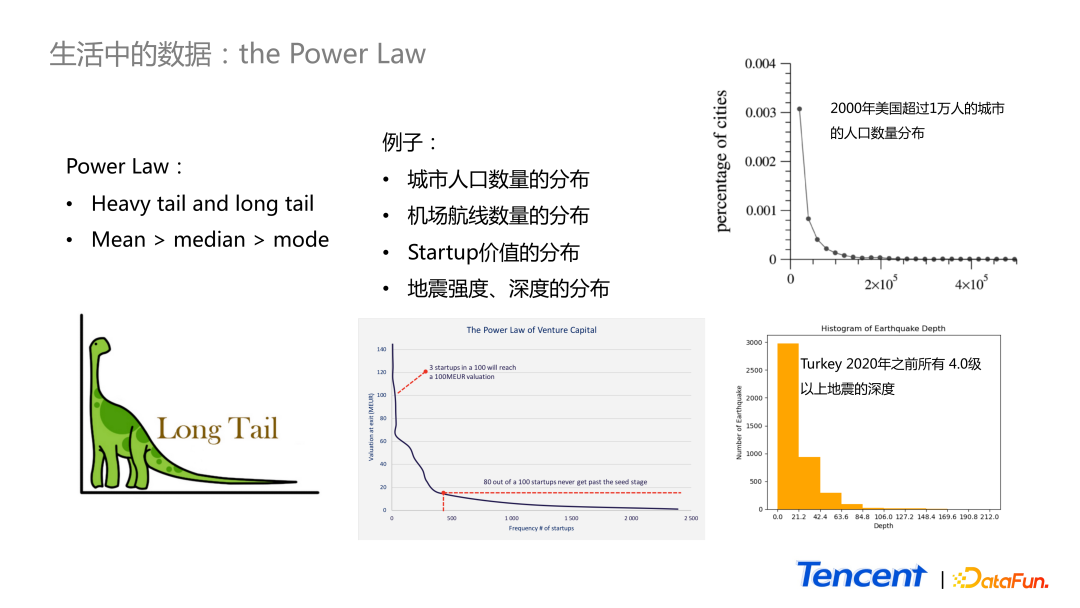
Power Law 分布如圖中雷龍的樣子,在較小的范圍里相對小的值有很高的概率出現,而右邊的尾巴很長,極大值可以很大,但出現的頻率卻很低。在這樣的分布里,因為存在極大值,所以其均值大于中位數大于眾數。舉一些例子:
- 常見的城市人口數量分布,2000 年美國超過 1 萬人的城市的人口數量分布,是一個很明顯的 Power Law 分布,大城市的數量極少。
- 在自然界中,地震深度的分布也屬于 Power Law 分布,比如上圖所示的 2020 年之前土耳其所有 4.0 級以上地震的深度的分布。
- Startup 價值的分布,那些 venture capital 真正想投資追逐的是最后的尾部,但凡能命中 top one,不會在意 top two。
為什么人們對 Power Law 的分布感知更強烈呢?比如提到城市人口數量,大家能馬上想到的大城市只有少數幾個,超過 2000 萬人的城市如北京、上海,小一些的 400 萬人口的城市如大連等。剩下一些非常小的城市,甚至想不起來名字,也不會在腦海里浮現出來。又比如每天上下班通勤中,大多數路口的車流量實際上并不高,只有個別路口非常堵。說起來哪最堵,大家心里都比較清楚。因此在日常生活中對 Power Law 感知更加強烈。
3、為什么 Power Law 常見?

為什么 Power Law 數據在日常生活中這么常見?
從抽象的角度來講,human-related networks 數據最終都會呈現出 Power Law 的情況。因為人類的喜好是有共性的,做出的選擇大多都是相似的,這導致了個別數據非常集中。
比如,我們可以把每個人想象成一個點,若在 Facebook 或者 Twitter 上有 follow 好友的關系,就將這兩點連線,最終呈現出如上圖 1 的關系。從內容生態角度而言,也可以把內容或創作者看作一個點,若同一個 c 端用戶消費內容就畫一條邊,最終呈現的也是如上圖 1 的樣子。所以這種有 pattern 的圖,每一個節點的邊的數量大概率呈現為 Power Law。而真正隨機產生的一個 network graph 則是像上圖 2。
這就是抽象機制。
理論機制也存在多種,這里舉 3 個例子:
Proportional random growth 機制
假設有固定數量的隨機變量,用 s 表示,每一個時間可取到的值=上一個時間的值 × 隨機變量 γ。這里面的 γ 是 iid 的隨機變量,有 pdf f,γ>0。在 t+1 時刻,隨機變量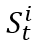 大于某一個固定值的概率,我們把它定義為 function
大于某一個固定值的概率,我們把它定義為 function 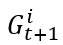 。它與
。它與 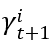 相關,所以如圖中間公式所示。最終可以寫成一個期望的形式,這個期望又可以展開成一個積分形式,因為已知 density function 是 f,如果滿足一定條件,system 最終會達到一個均衡狀態。均衡狀態是指 function G 不隨時間的變化而變化,就可把時間的角標去掉, 得出 function G 等于積分里面的 function G 等式。
相關,所以如圖中間公式所示。最終可以寫成一個期望的形式,這個期望又可以展開成一個積分形式,因為已知 density function 是 f,如果滿足一定條件,system 最終會達到一個均衡狀態。均衡狀態是指 function G 不隨時間的變化而變化,就可把時間的角標去掉, 得出 function G 等于積分里面的 function G 等式。
function G 的 solution 可以是什么形式?如果 function a over x to the power k 滿足積分等于 1 的條件下,function G 的 parameter k,能滿足積分形式的 G 就是最后等式的一個 solution。它恰好是一個 Power Law 分布的 1 減 CDF 的 function。所以在 proportional random growth 這種情況下,當系統達到均衡的狀態,會得到一個 Power Law 的分布。
Transformations of PLs
當我們對 Power Law 的 random variable 進行一些操作,比如把它們相加、相乘、取最小值或取最大值等。最終都會得到一個新的 Power Law 分布。
Matching and equilibriumn
第三個形成機制是經濟學的一個理論,叫做 matching。分享一個 CEO 工資的例子。
大家都知道 CEO 的工資都很高,而且大公司往往比小公司高了很多。這是為什么呢?
先來介紹背景,公式中的 n 代表公司的角標,S of n 表示第 n 個公司的規模;m 表示 CEO 候選人角標,T(m)表示 CEO 才華價值;ω(m) 表示第 m 個 CEO 候選人的薪水范圍。
針對每一個公司,都希望能最大化 T(m)-ω(m) 的差值。這里面還有一個參數 γ,表示大公司相對于小公司而言,在短時間內更難被 CEO 改變,即 γ<1。
若存在最優解,那么 objective function 的一階導數是 0,變量是 m,因此若對 t 取導,乘以它減去 γ 的導數,最終等于 0,于是得出一個表達形式。
在 paper 里面,基于歷史數據,researcher 對 s 的形式作了假設,假設公司規模服從帕累托分布,有參數 γ 對于 CEO 候選人的才華價值的導數,并且右側尾巴是滿足一定指數的。經過一番處理之后,最終得出上圖中的公式。
這篇 paper 里面,他們研究對象是世界 500 強的公司,按公司規模從大到小排序, n star 250 就是第 250 個公司。最后 paper 里做了一些 calibration,發現 γ 的值基本上就是 1,β 與 α 的比值約為 2: 3 。
還有一個有趣的結論,他們發現在最大的和中位數的公司中,兩者的 CEO 的才華價值差異小于 1% ,但是前者的工資卻是后者的 5 倍。這也解釋了為什么 CEO 的工資的分布屬于 Power Law。
另外也從側面印證了,在許多優化問題里,若原始的數據存在 Power Law 分布,它最后的結果很可能也是 Power Law 的分布。
4、內容生態數據:the Power Law
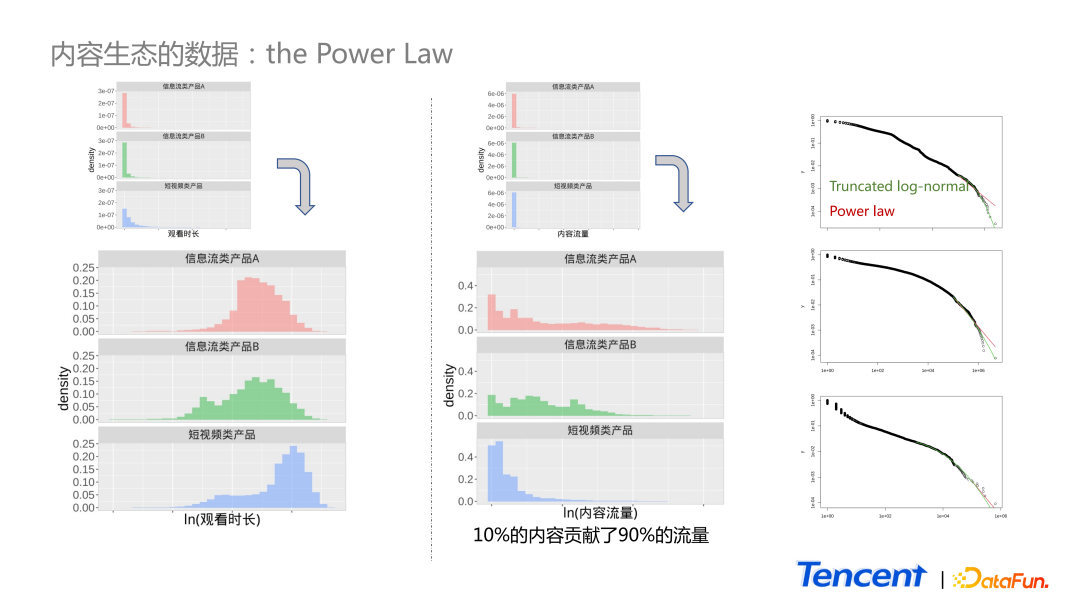
如圖中所示,展示了 3 個產品 c 端用戶單天消費時長的分布。這里選了 3 個產品,藍色的圖為短視頻產品,紅色和綠色為信息流類的產品。
上面小圖是原始數據的分布,由于第一個柱子特別高,無法查看具體的 pattern,因此取了對數進行分析,取對后發現均類似鐘型的對稱分布。
中間的圖與左側圖類似,中間圖為內容流量的分布,依舊看不出什么 pattern。取對后發現,它依舊是 Power Law 形式的分布,右側有一個長尾巴,大部集中在前面比較小的范圍里。所以對比單天的用戶消費時長和內容流量的分布,是類似的,其實在我們的生態里面,10% 的內容貢獻了 90% 的流量。
大多數時候,大家遇到右側尾部很長的分布,會對尾部更感興趣。比如對這三個數據,分別用 truncated,log normal 還有 Power Law 對它們做擬合。但并未發現 Power Law 或 log normal 的顯著優勢。
二、我們可以做什么?
1、厚尾分布及其性質
當我們看到 Power Law 的數據,可以做些什么呢?
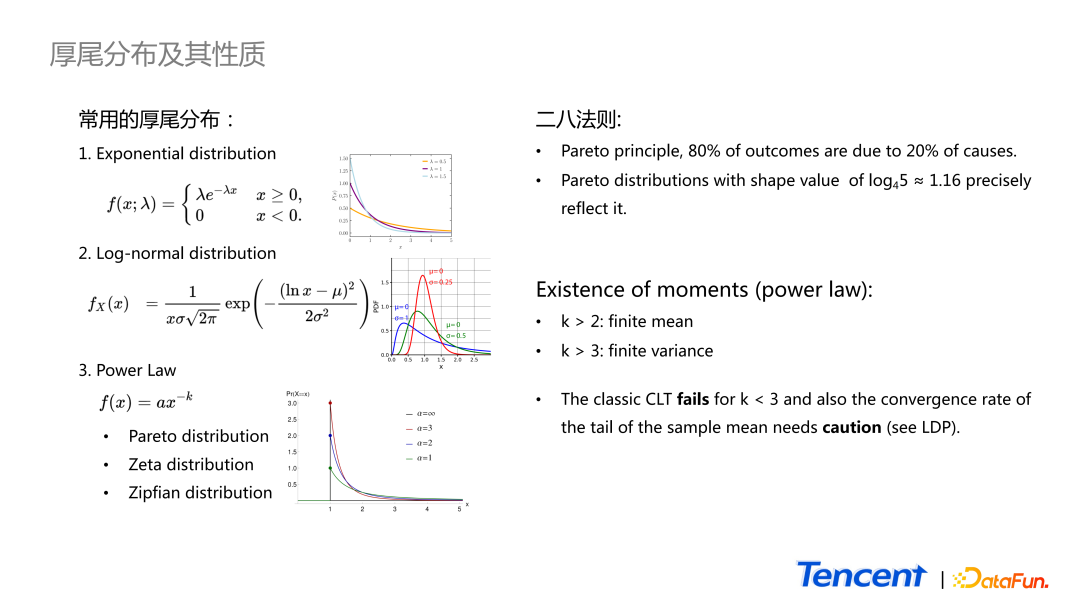
先來看 Power Law 分布具體的定義和性質。基本上看到與雷龍相似的分布就認為是Power Law。但這只是一個比較通用的概念。準確來說,我們只能說它是一個厚尾分布。厚尾分布根據尾巴的厚度從薄到厚,常用的有以下三種:
- 第一種是大家熟悉的指數分布。
- 尾巴稍微厚一點的就是 Log-normal 分布,就是隨機變量 take log 之后是正態的,所以它就是一個 log-normal distribution。常用的是 truncate 以后的 version,比如我們更關心它右側長的是什么樣子的。
- 最后一個指的是一類分布,最著名的例子就是帕累托分布,還有 Zeta 分布、Zipfian 分布。
Power Law 分布有如下性質:
其中最著名的就是二八法則,又稱為 Pareto principle。表示 80% 的結果均由 20% 的原因造成的。更準確地講,它是一個特殊的帕累托分布,所產生的現象就是 ship parameter 等于 1.16 的帕累托分布。在日常工作中,我們可以花更多的精力和資源去抓住重要的 20%,這樣就能拿到大部分的收益。
第二個性質是針對整個 Power Law 的,當參數 k 大于 2,它才有 finite mean;當參數 k 大于 3,它才有 finite variance。這就存在一些潛在問題,如應用很廣的理論 central limit theorem,它要求隨機變量的均值和方差都是定義良好的。但若 Power Law 存在,且 variance 不在有限的情況下,會導致 central limit theorem 失效;或者是 variance 很大的時候,其收斂速度會很慢。另外一個問題是,central limit theorem 只描述了 sample mean 中心部分分布的樣子,它會最終收斂成正態分布,但并不關注尾部特征。對這部分感興趣的同學可以看一下大偏差理論 large deviation principle。
Power Law 的這兩個性質,可能會在日常應用中帶來一些風險。比如在 AB 實驗中,可能因為個別極端值的存在,導致 AB 分組本身存在一定的差異。
第二個問題是 10-Sigma event 會比我們預想中更容易發生。有一個經典的例子,在 1998 年時,名為 long term capital management 的對沖基金因為假設了某個貨幣的一些 movements 是服從正態分布的,從而低估了風險,結果發生了 10-Sigma event 的發生,這是一個小概率的事情,但導致了他們破產。
2、Power Law 應用例子
(1)網頁搜索瀏覽

第一個例子,谷歌的網頁瀏覽量基本上是服從 Zipf’s law。谷歌在做網頁索引時,最高優的索引池的量級是相對較小的,只有百萬級別,網頁的索引可以達到秒級的更新。而谷歌的全量索引池是千億級別的,只能達到小時或者天級的更新。即便是這樣,只有一個規模如此之小的高優索引池,也可讓谷歌的搜索提供高質量的搜索體驗,就是因為 Zipf’s law 的存在。
另外一個原因是,部分網頁不需要更新這么快,比如 Wikipedia 中線性規劃的網頁,質量很高,但更新頻率很慢,而且不會存在顛覆性的更新,所以即便它是一個好的網頁,也不需要進最高優的索引池。一般只有新聞或者是體育賽事的實況信息才需進入高優搜索池。
第二個例子也與搜索相關,現在很多搜索結果都是在右上方 knowledge panel,只有一小部分會被高頻率地訪問到。因此只有這些 hot part 才會被頻繁地更新,而那些 cold part 更新速度比較慢。
我們可以將這兩個優點利用得很好,但需要注意 Power Law 帶來的問題。
比如大家以 URL 為單位,以點擊量作為觀測數據進行 AA 實驗,即便是百萬量級,最后也可能因為一兩個網頁導致均值上顯著的差異。因此在谷歌絕大部分實驗都是以 query 為單位進行的。為了克服這個問題還有其他方法,拿到實驗數據時并不能直接得出結論,而是需要進一步做一些分析,常用分析方法有 DID、propensity score matching 或者是 propensity score weighting 等。
(2)書店對比
第二個例子是兩個書店的對比。
Barnes & noble 是美國常見的連鎖實體書店。Amazon 是電商。Barnes & noble 的藏書量僅幾十萬本,但是亞馬遜只有 30% 銷售的是 Barnes & noble 沒有的書。正因為二八法則的存在,這樣小的實體書店才得以存活下來,并且規模是越來越大。這就類似阿基米德說的,給一個杠桿,就能敲起地球。
三、我們是怎么做的?
1、內容中臺:全鏈路統籌優化,以小換大
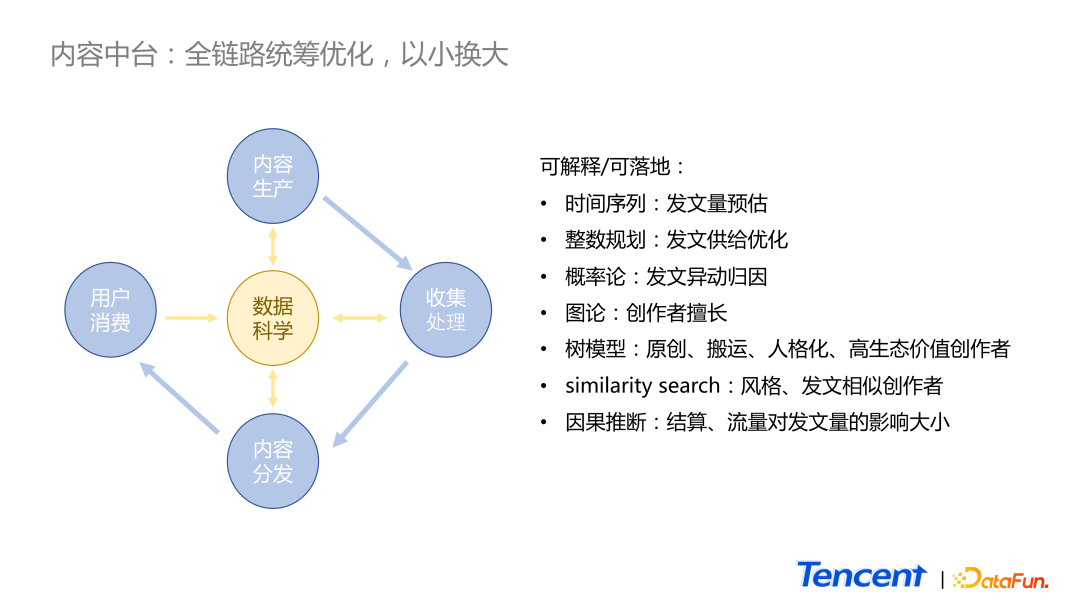
如圖所示,在傳統的內容生態行業里,供應鏈流程如下:
- 首先需要內容創作者進行內容生產。
- 然后業務將數據收集并進行進一步的加工,如安全性、分類、打 tag 等。
- 接著進入推薦或者搜索的場景進行分發。
- 最終才能觸達到 c 端的用戶。
在傳統的供應鏈里,每一個環節只能接觸到上游或者下游的數據,很難做到全鏈路的統籌優化。而在數據科學中心則會得到全業務鏈路每一個環節的數據,因此我們可以做的優化工作有很多。舉 3 個偏傳統統計和概率的例子:
- 內容生產環節上,可以通過時間序列進行發文預估,甚至可進一步地讓業務對各自的進行預算預估和分配資源。
- 通過整數規劃找到一些相對不重要的內容或創作者,調整策略。
- 概率論的應用,實現自動對發文量的異動進行歸因,節省了人力的成本。
在信息內容的收集和處理環節也有很多比較偏算法的項目:
- 用圖論描述創作者是什么樣子的。比如一個創作者他擅長的話題和程度,或者表示原創、搬運或人格化程度很高等。
- 通過樹模型,對創作者進行發文和創作的風格或相似性進行對比。
- 通過因果推斷找到對創作者產生影響的抓手。
2、策略優化
我們常用流量補貼政策、流量補貼策略和結算補貼策略激勵創作者,因此希望知道這些策略對創作者的影響大小。以下分享 3 個日常工作中的案例。
(1)整數規劃

這是一個發文策略中整數規劃的例子。
這個項目是為了找到高生態價值的頭部作者,從而進行補貼策略的調整。r 表示業務的收益函數,c 表示成本函數。在絕大多數情況下,收益函數都是 concave 的函數,成本函數都是一個 convex 的形式,所以 objective function 形式比較好。最后是一個 concave,很適合做 maximization。
這里有一些 constraints。我們不希望業務對創作者產生過大的影響,因此對于每一個業務和賽道,需要有一個限制。這里面的 x1 到 xn 表示有 n 個創作者,如果等于 1,需要進入到新策略里,若等于 0 就不放到新策略里。通常來講 function r 和 function c 形式是多變的,但我們可以用 piecewise linear function 進行預估。圖中可看出最終這個問題就會轉化成一個形式非常好的混合的整數規劃,可以用 branch and cut 方法進行求解,能保證理論上有唯一的最優解。
(2)創作者擅長領域定義 & 挖掘
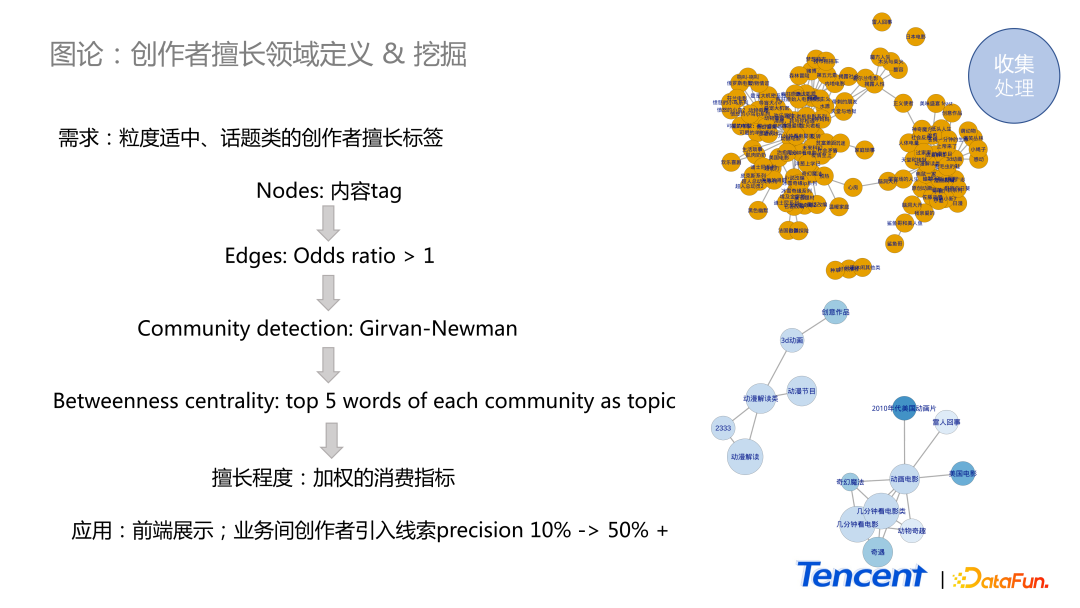
第二個例子是圖論里的方法的應用,我們希望對創作者擅長的領域進行描述,并且對其擅長度進行打分。
在我們的體系里,對于創作者的內容可分成兩類:
- 按類型分類,約有幾百個類型。
- 按 tag 分類,至少有幾百萬的量級。
對于運營同學而言,幾百量級的分類,顆粒度太粗,而幾百萬的 tag 分類, 顆粒度又太細,很難直觀地描述創作者適合創作什么話題。
因此我們針對每一個創作者,將他過去一段時間內的發文的 tag 取出來。每一個 tag 作為一個節點。我們把節點 a 和節點 b 當作兩個隨機事件,若其中一個發生使得另一個事件更容易發生,即認為它們之間存在正相關性,在兩個節點之間連上一條線。我們可以用 odds ratio 來度量這個關系,若它大于 1,就給它們之間連上線。接下來用一個比較經典的 community detection 的方法去對它進行分析。可將社區看作是創作者常創作的話題,有社區之后,我們可以找中心度比較高的詞,并認為這些些詞能夠抽象地描述出這個話題是什么。最后,我們用一個加權的消費指標,描述在話題里作者的擅長程度。
圖中黃色點是一個創作者原始的數據,下方是經過處理后最終得到的結果。可以看出,創作者擅長創作兩類話題,一類是動畫電影的解讀,一類是動漫類作品的解讀。這個結果提高了不同業務之間創作者引入索引的準確性,從 10% 提高了至 50%。
3、結算策略變化對創作者的影響
通過數據分析和算法模型,我們對創作者的基本畫像有了概念,那么如何推動不同類型的創作者調整他們的行為呢?
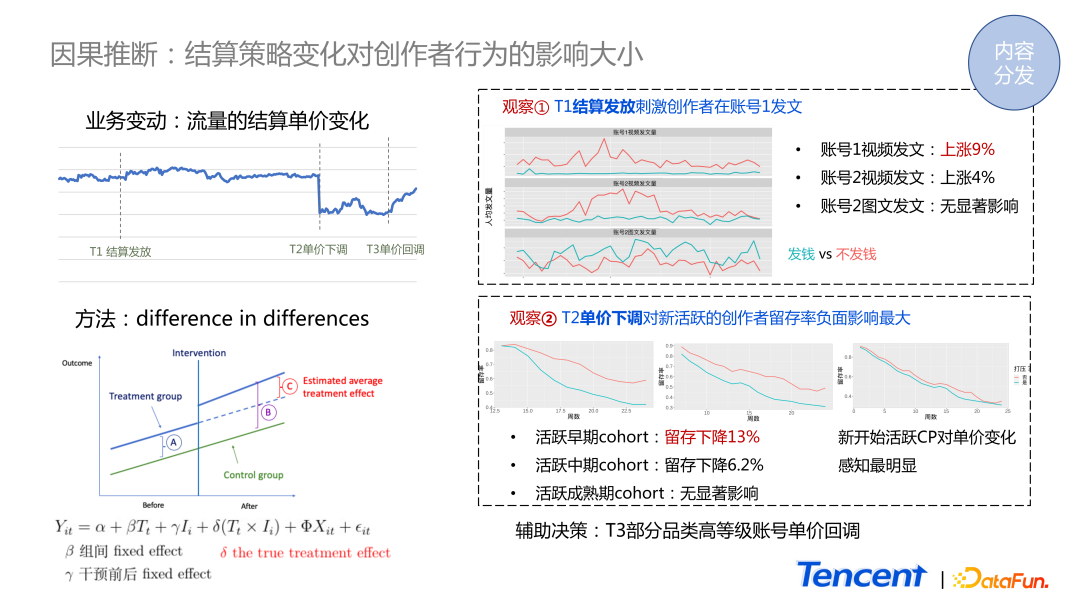
其中一個因素是結算策略的變化。我們希望知道結算策略的變化對創作者有什么影響,影響有多大。如圖所示,這是某一個視頻業務的賬號體系的結算單價數據,從 T1 時刻開始結算發放,到 T2 時刻下調單價。我們想知道這兩個行為在創作者側產生了怎樣的影響。
創作者對結算金額是非常敏感的,無法進行傳統的 AB 實驗,若因他屬于實驗組就被削減了單價,是非常不公平的。因此在這個場景下,我們只能對歷史數據進行因果推斷。
最經典常用的方法是 DID,受干預的組和沒有受干預的組在干預之前,創作者因本身的差異,導致我們所關心的指標產生差距 A。在 intervention 發生后,這兩組的差距變成了 B。在 AB 實驗場景里,可能只對 intervention 發生之后的數據進行對比,得到差異值是 B。但實際上 intervention 自己本身產生的影響是 B 減去 A,所以 C 才是我們真正想知道的值。
DID 方法的應用有兩種情況:
- 單純地計算差的差。先算 B 的值,再算下 A 的值。兩個相減后,再做一些統計上的 test,觀察差異是否顯著。如果是,說明這個 intervention 是有影響的,并且知道影響的大小。
- 第二種應用方式是把它放到一個線性回歸里面。T 代表時間,intervention 會產生一個時間點。i 表示兩組分別屬于被干預組,還是沒有受到干預的組。重點是變量 x ,我們可以把一些用戶的屬性數據看作 x,如賬號的年紀、賬號的類型等,從而將這種 intervention 的影響分析得更清楚。
右側是我們分析的結果:
- 在 T1 時刻,賬號體系 A 發放結算使得他們的視頻發文量顯著提升 9%,同樣,另外一個賬號體系的視頻發文量也顯著地上升,而對圖文賽道卻沒有影響。
- 在 T2 時刻單價下調后,發現對剛開始活躍的新賬號創作者而言,他們的體感是最強的,其留存率下降 13%。而對于活躍中期的用戶,留存的下降就沒那么明顯,而成熟期的基本沒有產生影響。
這兩個觀察結論輔助了業務進行決策,決定在 T3 時刻對部分的高等級賬號進行單價的回調。

四、問答環節
Q1:在日常的生活工作中,基于分布給出估計的前提是我們知道數據符合什么樣的分布。在無法直觀判斷分布的前提下,我們應該怎么處理數據,使其可以滿足我們后續預測的需求?
A1:首先都會有一個直觀的感受。比如我們可以先畫下 Histogram,大概看一下它長成什么形狀。大多數情況下,這些分布是有參數的,如正態是有參數的,這些 power law也是有參數的。我們可以用 maximum likelihood 對參數進行估計,然后用這些參數可以做一個 simulation,查看這個分布下產生的數據是什么樣子的。相當于我們有了兩組數據,進而我們又可以做 Kolmogorov Smirnov test,查看兩組分布是否存在顯著的差異。如果沒有顯著的差異,即證明我們 calibrate 出來分布能滿足所需。
但實際中常出現一種情況,如上面所提到的例子,一般 log normal 和 Power Law 上最后的結果都差不多。所以在這種情況下,不管是用 log normal 還是用 Power Law 都可以。
Q2:請問對于符合 Power Law 分布的總體來說,在后續建模中,如果過分提高頭部樣本的權重,對長尾部分樣本的權益存在一定的不公平,在實際業務中會引起長尾用戶的反感。該如何規避建模時這種情況的發生呢?
A2:實際上,在我們的業務里,前期在做數據分析時并不會規避這些東西。比如想找到哪些相對不重要的內容,我們就會認認真真地做分析找出結論。但在做策略時,會考慮這些問題,在策略的設計上做得比較溫和。