用 Java 深入研究樹,你了解多少?

樹數據結構在我們編碼和面試中都是很重要的知識。使用數據結構來組織數據,數據結構越高效,程序就會越好。
今天,我們將深入探討數據結構之一:樹。
今天,我們將介紹:
- 什么是樹?
- 樹的種類
- 樹的遍歷和搜索
什么是樹?
數據結構用于存儲和組織數據。我們可以使用算法來操縱和使用我們的數據結構。通過使用不同的數據結構可以更有效地組織不同類型的數據。
樹是非線性數據結構。它們通常用于表示分層數據。舉一個現實的例子,分層的公司結構使用樹來組織。
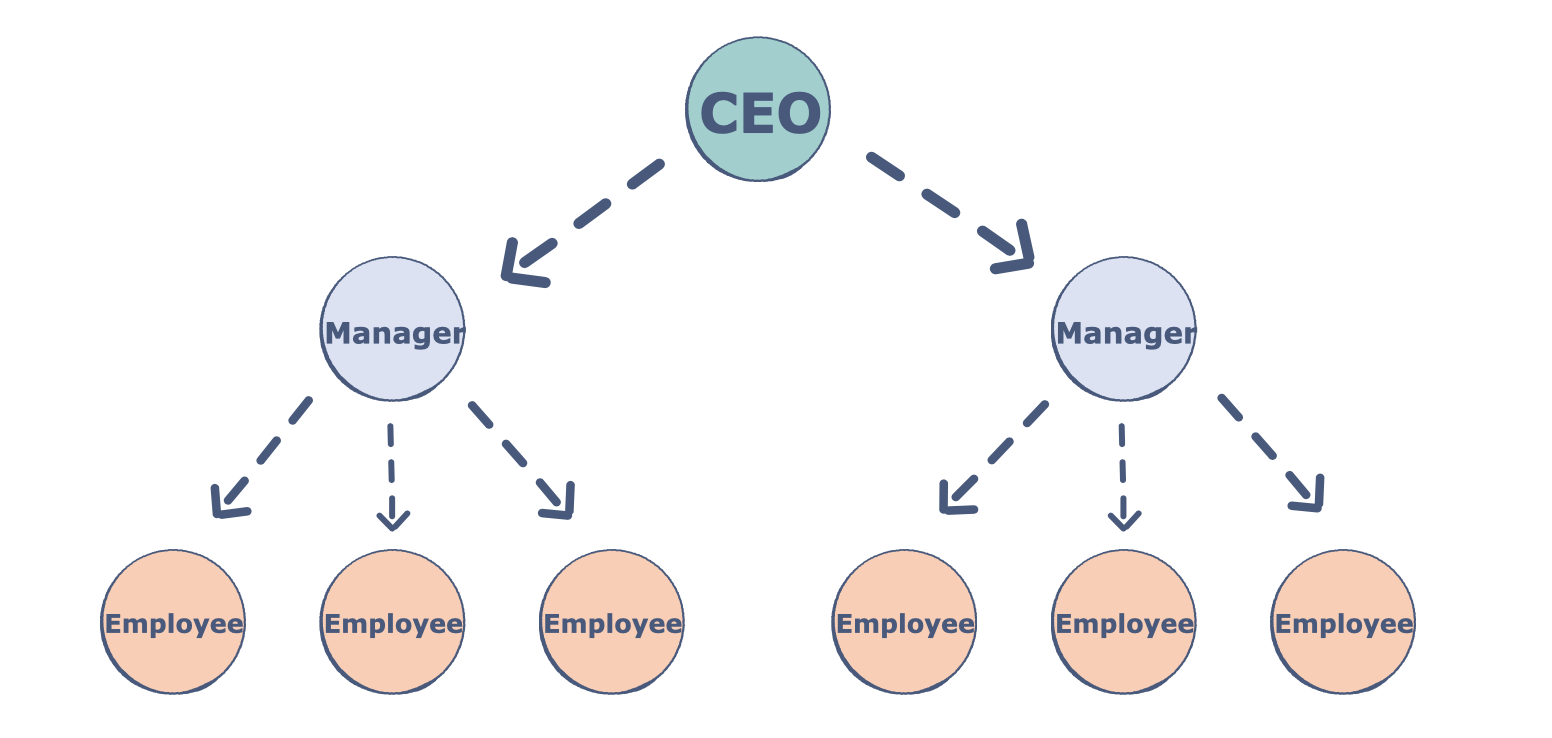
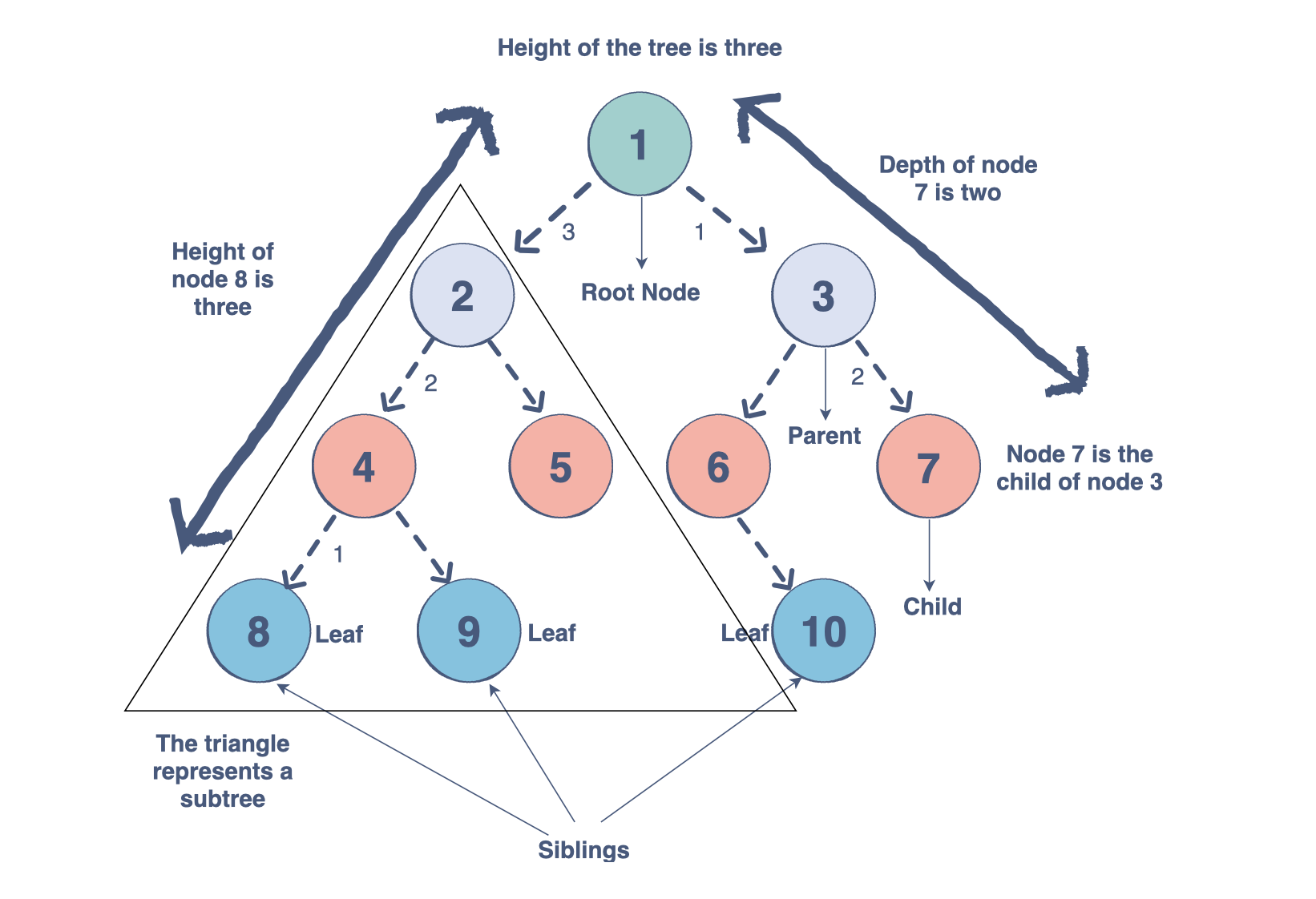
樹的組成部分
樹是節點(頂點)的集合,它們通過邊(指針)鏈接起來,代表節點之間的層次連接。節點包含任意類型的數據,但所有節點必須具有相同的數據類型。樹與圖類似,但樹中不能存在環。樹有哪些不同的組成部分?
根:樹的根是沒有傳入鏈接的節點(即沒有父節點)。將此視為樹的起點。
子節點:樹的子節點是一個節點,具有來自其上方節點(即父節點)的一個傳入鏈接。如果兩個子節點共享同一個父節點,則它們稱為兄弟節點。
父節點:父節點具有將其連接到一個或多個子節點的傳出鏈接。
葉子:葉子有一個父節點,但沒有到子節點的傳出鏈接。將此視為樹的端點。
子樹:子樹是包含在較大樹中的較小樹。該樹的根可以是較大樹中的任何節點。
深度:節點的深度是該節點與根之間的邊數。將此視為節點和樹的起點之間有多少步。
高度:節點的高度是從該節點到葉節點的最長路徑中的邊數。將此視為節點和樹端點之間有多少步。樹的高度是其根節點的高度。
度:節點的度是指子樹的數量。
我們為什么要使用樹?
樹可以應用于很多事情。層次結構賦予樹用于存儲、操作和訪問數據的獨特屬性。樹構成了計算機最基本的組織結構。我們可以將樹用于以下用途:
- 存儲為層次結構。存儲層次結構中自然出現的信息。計算機上的文件系統和 PDF 使用樹結構。
- 搜索。存儲我們想要快速搜索的信息。樹比鏈表更容易搜索。某些類型的樹(如 AVL 樹和紅黑樹)是為快速搜索而設計的。
- 繼承。樹可用于繼承、XML 解析器、機器學習和 DNS 等。
- 索引。高級類型的樹(例如 B 樹和 B+ 樹)可用于為數據庫建立索引。
- 網絡。樹非常適合社交網絡和電腦國際象棋游戲等。
- 最短路徑。生成樹可用于查找路由器中的最短路徑以進行網絡連接。
- 等等
如何編碼一棵樹
例如,要在Java中構建樹,我們從根節點開始。
Node<String> root = new Node<>("root");一旦我們有了根,我們就可以使用添加第一個子節點addChild,這會添加一個子節點并將其分配給父節點。我們將此過程稱為插入(添加節點)和刪除(刪除節點)。
Node<String> node1 = root.addChild(new Node<String>("node 1"));我們繼續使用相同的過程添加節點,直到我們擁有復雜的層次結構。
樹的種類
我們可以使用多種類型的樹在層次結構中以不同的方式組織數據。我們使用的樹取決于我們要解決的問題。讓我們看一下可以在 Java 中使用的樹。我們將涵蓋:
- N叉樹
- 平衡樹
- 二叉樹
- 二叉搜索樹
- AVL樹
- 紅黑樹
- 2-3 棵樹
- 2-3-4 樹
N叉樹
在N叉樹中,一個節點可以有0-N個子節點。例如,如果我們有一個二叉樹(也稱為二叉樹),它最多有 0-2 個子節點。
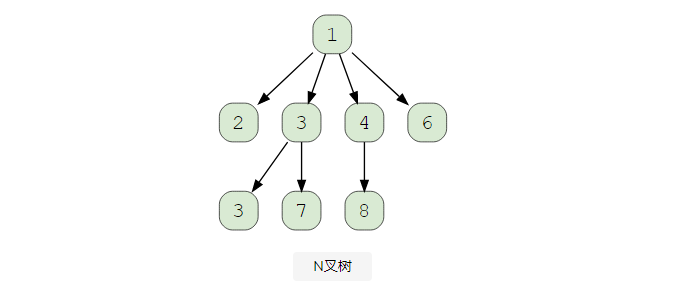
注: 節點的平衡因子是左右子樹的高度差。
平衡樹
平衡樹是幾乎所有葉子節點都在同一級別的樹,最常應用于子樹,即所有子樹都必須是平衡的。換句話說,我們必須使樹高平衡,左右子樹的高度差不超過1。這是平衡樹的直觀表示。
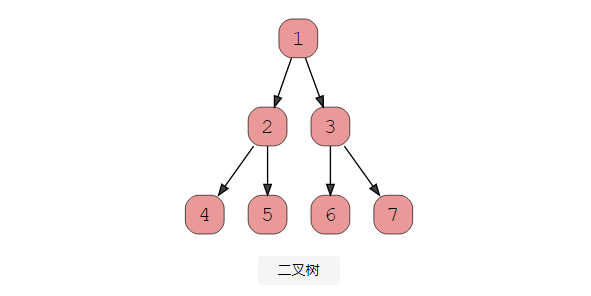
根據其結構,二叉樹主要分為三種類型。
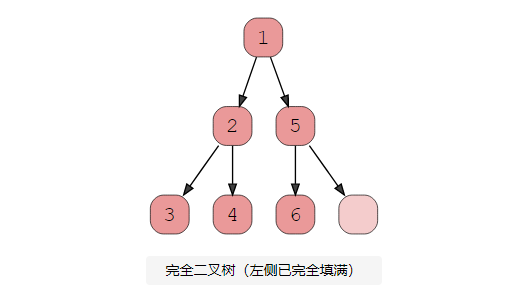
1、完全二叉樹
當每一層(不包括最后一層)都被填滿并且最后一層的所有節點都盡可能靠左時,就存在完全二叉樹。這是完整二叉樹的直觀表示。
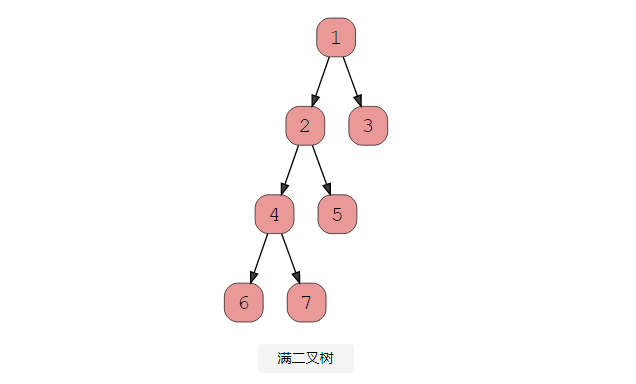
2、滿二叉樹
當每個節點(不包括葉子)都有兩個子節點時,就存在滿二叉樹(有時稱為真二叉樹)。每一層都必須填滿,并且節點盡可能遠離。查看此圖以了解完整二叉樹的外觀。
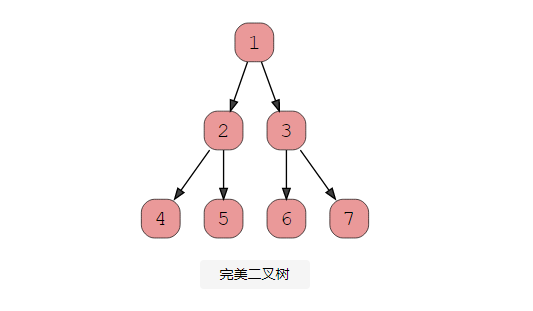
3、完美二叉樹
完美的二叉樹應該是滿的和完整的。所有內部節點都應該有兩個子節點,并且所有葉子節點必須具有相同的深度。查看此圖以了解完美二叉樹的外觀。
注意:還可以擁有傾斜二叉樹,其中所有節點都向左或向右移動,但最佳實踐是在 Java 中避免這種類型的樹,因為搜索節點要復雜得多。
二叉搜索樹
二叉搜索樹是一棵二叉樹,其中每個節點都有一個鍵和一個關聯值。這允許快速查找和編輯(添加或刪除),因此得名“搜索”。二叉搜索樹根據其node值有嚴格的條件。需要注意的是,每個二叉搜索樹都是二叉樹,但并非每個二叉樹都是二叉搜索樹。
是什么讓他們與眾不同?在二叉搜索樹中,子樹的左子樹必須包含鍵少于該節點鍵的節點,而右子樹將包含鍵大于該節點鍵的節點。查看此視覺效果以了解這種情況。
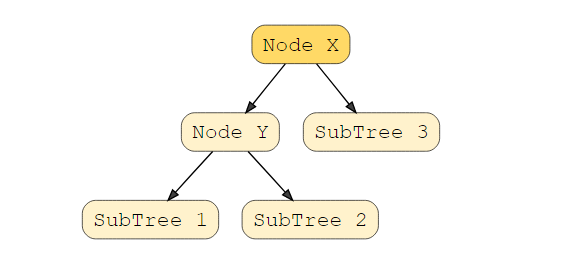
在此示例中,節點 Y 是具有兩個子節點的父節點。子樹 1 中的所有節點的值必須小于節點 Y,子樹 2 中的所有節點的值必須大于節點 Y。
AVL樹
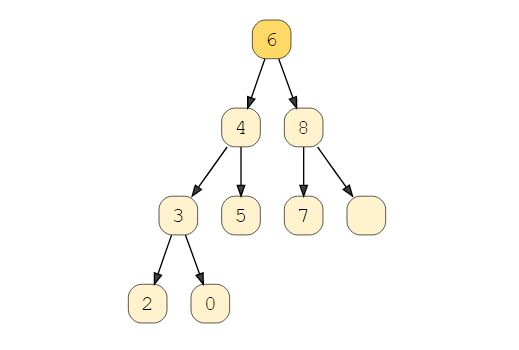
AVL樹是一種特殊類型的二叉搜索樹,它通過檢查每個節點的平衡因子來實現自平衡。平衡因子應該是+1、0或-1。左右子樹的最大高度差只能為1。
如果這種差異變得大于一個,我們必須使用旋轉技術重新平衡我們的樹以使其有效。這些對于搜索是最重要操作的應用程序來說是最常見的。查看此視覺效果可以看到有效的 AVL 樹。
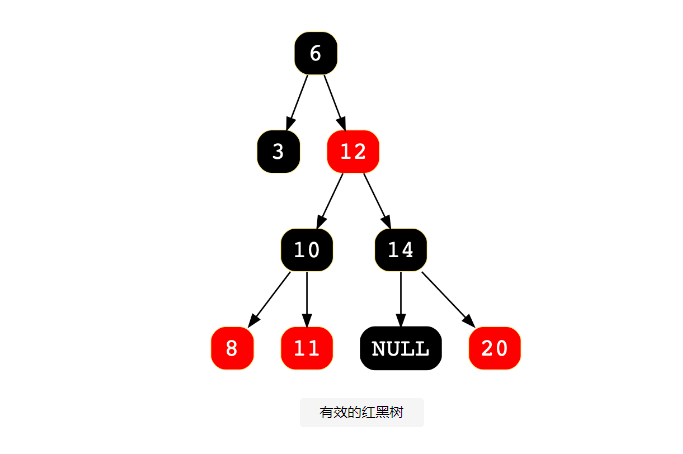
紅黑樹
紅黑樹是另一種自平衡二叉搜索樹,但它具有 AVL 樹的一些附加屬性。節點的顏色為紅色或黑色,以幫助在插入或刪除后重新平衡樹。它們可以節省平衡時間。那么,我們如何為節點著色呢?
- 根部始終是黑色的。
- 兩個紅色節點不能相鄰(即紅色父節點不能有紅色子節點)。
- 從根到葉的路徑應包含相同數量的黑色節點。
- 空節點是黑色的。
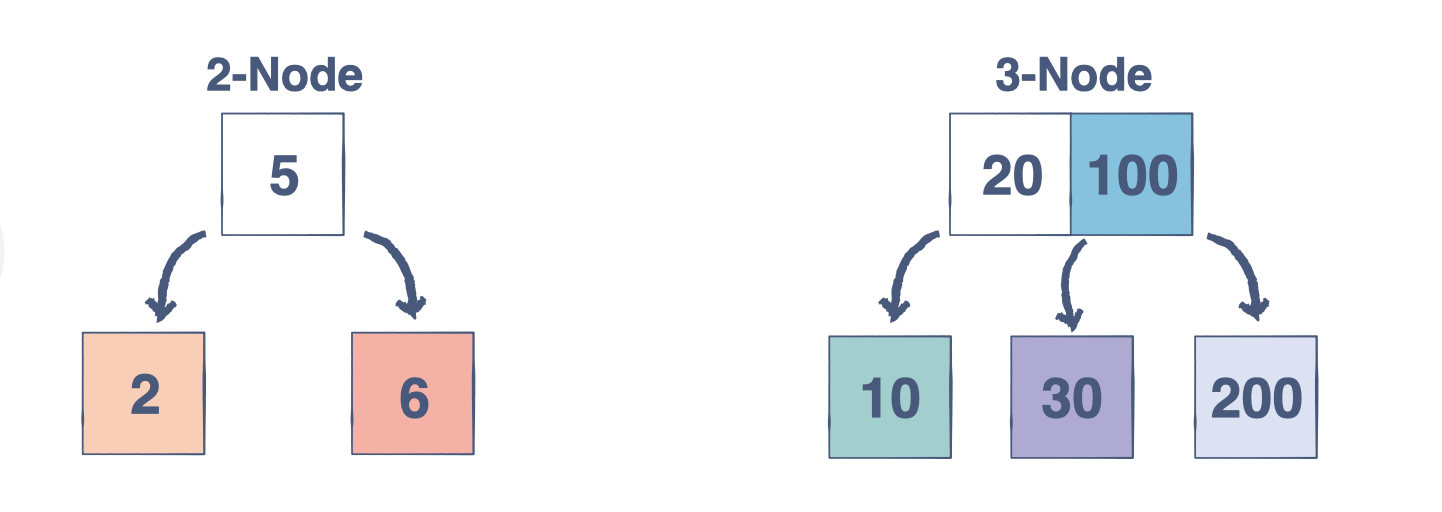
2-3 棵樹
2-3 樹與我們目前學到的有很大不同。與二叉搜索樹不同,2-3 樹是一種自平衡、有序、多路搜索樹。它始終是完美平衡的,因此每個葉節點與根的距離相等。除葉節點外,每個節點都可以是 2 節點(具有單個數據元素和兩個子節點的節點)或 3 節點(具有兩個數據元素和三個子節點的節點)。無論發生多少次插入或刪除,2-3 樹都會保持平衡。
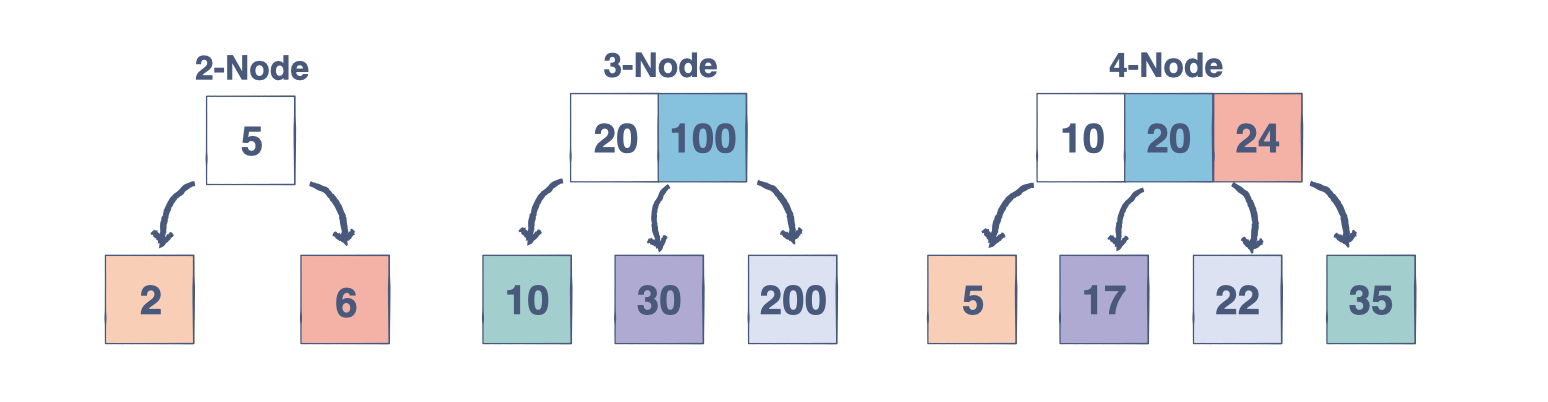
2-3-4 樹
2-3-4 樹是一種比 2-3 樹可以容納更多鍵的搜索樹。它涵蓋了與 2-3 樹相同的基礎知識,但添加了以下屬性:
- 2-節點有兩個子節點和一個數據元素
- 3-Node 有三個子節點和兩個數據元素
- 4-節點有四個子節點和三個數據元素
- 每個內部節點最多有 4 個子節點
- 對于內部節點的三個鍵,LeftChild節點的所有鍵都小于左鍵
- LeftMidChild 上的所有鍵都小于中間鍵
- RightMidChild 處的所有鍵都小于右側鍵
- RightChild 處的所有鍵都大于右側鍵
樹遍歷和搜索簡介
要使用樹,我們可以通過訪問/檢查樹的每個節點來遍歷它們。如果一棵樹被“遍歷”,這意味著每個節點都被訪問過。遍歷一棵樹有四種方法。這四個過程屬于兩類之一:廣度優先遍歷或深度優先遍歷。
- 中序:將其視為在樹上向上移動,然后向下移動。遍歷左子樹及其子樹,直到到達根。然后,向下遍歷右孩子及其子樹。這是深度優先遍歷。
- 前序:從根開始,遍歷左子樹,然后移動到右子樹。這是深度優先遍歷。
- 后序:從左子樹開始,移至右子樹。然后,向上移動訪問根節點。這是深度優先遍歷。
- 層序:將其視為一種之字形圖案。這將按節點的級別而不是子樹遍歷節點。首先,我們訪問根并從左到右訪問該根的所有子節點。然后我們向下移動到下一個級別,直到到達沒有子節點的節點。這是左節點。這是廣度優先的遍歷。
那么,廣度優先遍歷和深度優先遍歷有什么區別呢?讓我們看一下深度優先搜索 (DFS) 和廣度優先搜索 (BFS) 算法,以便更好地理解這一點。
注意:算法是用于執行某些任務的指令序列。我們使用具有數據結構的算法來操作我們的數據,在本例中是遍歷我們的數據。
深度優先搜索
概述:我們沿著從起始節點到結束節點的路徑,然后開始另一條路徑,直到訪問完所有節點。這通常使用堆棧來實現,并且它比 BFS 需要更少的內存。它最適合拓撲排序,例如圖回溯或循環檢測。
算法步驟DFS如下:
- 選擇一個節點。將所有相鄰節點壓入堆棧。
- 從該堆棧中彈出一個節點并將相鄰節點推入另一個堆棧。
- 重復此步驟,直到堆棧為空或達到目標為止。當訪問節點時,必須在繼續之前將其標記為已訪問,否則將陷入無限循環。
廣度優先搜索
概述:我們逐級訪問一級的所有節點,然后再進入下一級。BFS算法通常使用隊列來實現,并且它比DFS算法需要更多的內存。最適合尋找兩個節點之間的最短路徑。
算法步驟BFS如下:
- 選擇一個節點。將所有相鄰節點放入隊列中。將節點出隊,并將其標記為已訪問。將所有相鄰節點放入另一個隊列中。
- 重復此操作,直到隊列中沒有已實現的目標。
- 當訪問節點時,必須在繼續之前將其標記為已訪問,否則將陷入無限循環。
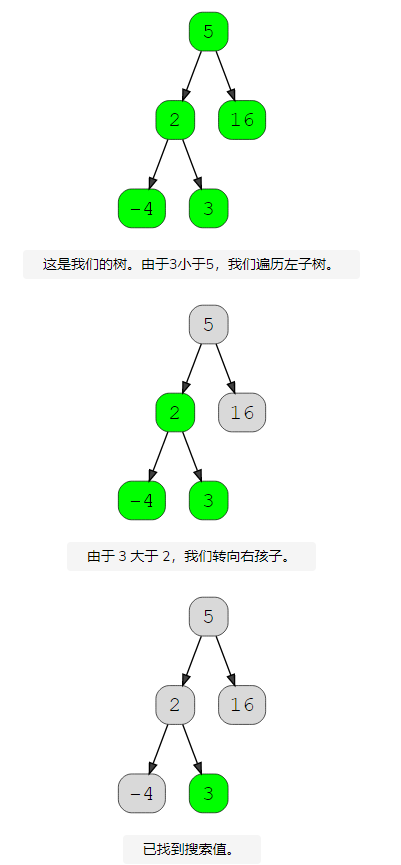
在二叉搜索樹中搜索
了解如何在樹中執行搜索非常重要。搜索意味著我們在數據結構中定位特定元素或節點。由于二叉搜索樹中的數據是有序的,因此搜索非常容易。讓我們看看它是如何完成的。
- 從根開始。
- 如果該值小于當前節點的值,則遍歷左子樹。如果大于,則遍歷右子樹。
- 繼續此過程,直到到達具有該值的節點或到達葉節點,這意味著該值不存在。
在3.中步驟,如下:
現在讓我們看看 Java 代碼中的內容!
public class BinarySearchTree {
…
public boolean search(int value) {
if (root == null)
return false;
else
return root.search(value);
}
}
public class BSTNode {
…
public boolean search(int value) {
if (value == this.value)
return true;
else if (value < this.value) {
if (left == null)
return false;
else
return left.search(value);
} else if (value > this.value) {
if (right == null)
return false;
else
return right.search(value);
}
return false;
}
}總結
本篇讓我們更深入了解樹的數據結構以及用的運用。