大型語言模型（LLM）通常擁有數十億的參數，用了數萬億 token 的數據進行訓練，這樣的模型訓練、部署成本都非常高。因此，人們經常用各種模型壓縮技術來減少它們的計算需求。

一般來講，這些模型壓縮技術可以分為四類：蒸餾、張量分解（包括低秩因式分解）、剪枝和量化。其中，剪枝方法已經存在了一段時間，但許多方法需要在剪枝后進行恢復微調（RFT）以保持性能，這使得整個過程成本高昂且難以擴展。

為了解決這一問題，來自蘇黎世聯邦理工學院、微軟的研究者提出了一個名為 SliceGPT 的方法。SliceGPT 的核心思想是刪除權重矩陣中的行和列來降低網絡的嵌入維數，同時保持模型性能。

研究人員表示，有了 SliceGPT，他們只需幾個小時就能使用單個 GPU 壓縮大型模型，即使沒有 RFT，也能在生成和下游任務中保持有競爭力的性能。目前，該論文已經被 ICLR 2024 接收。

• 論文標題：SLICEGPT: COMPRESS LARGE LANGUAGE MODELS BY DELETING ROWS AND COLUMNS
• 論文鏈接：https://arxiv.org/pdf/2401.15024.pdf

剪枝方法的工作原理是將 LLM 中權重矩陣的某些元素設置為零，并（選擇性地）更新矩陣的周圍元素以進行補償。其結果是形成了一種稀疏模式，這意味著在神經網絡前向傳遞所需的矩陣乘法中，可以跳過一些浮點運算。

運算速度的相對提升取決于稀疏程度和稀疏模式：結構更合理的稀疏模式會帶來更多的計算增益。與其他剪枝方法不同，SliceGPT 會剪掉（切掉！）權重矩陣的整行或整列。在切之前，他們會對網絡進行一次轉換，使預測結果保持不變，但允許剪切過程帶來輕微的影響。

結果是權重矩陣變小了，神經網絡塊之間傳遞的信號也變小了：他們降低了神經網絡的嵌入維度。

下圖 1 將 SliceGPT 方法與現有的稀疏性方法進行了比較。

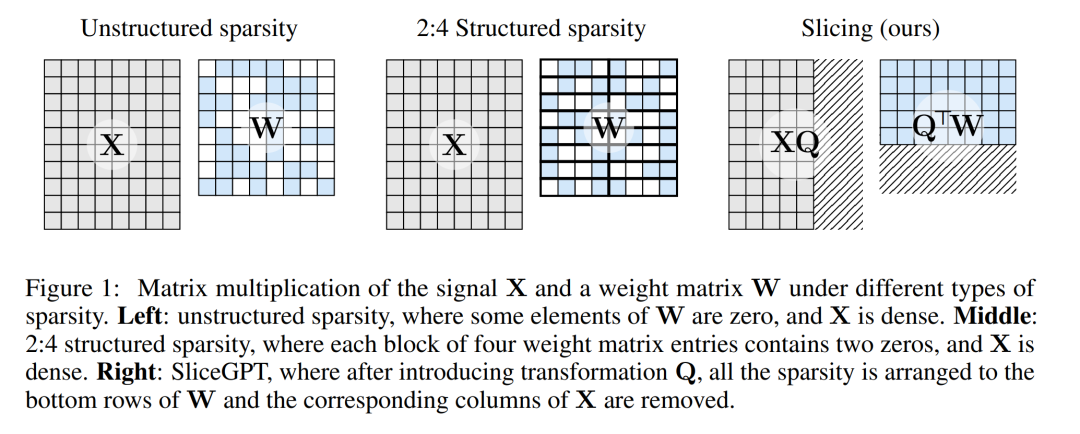
通過大量實驗，作者發現 SliceGPT 可以為 LLAMA-2 70B、OPT 66B 和 Phi-2 模型去除多達 25% 的模型參數（包括嵌入），同時分別保持密集模型 99%、99% 和 90% 的零樣本任務性能。

經過 SliceGPT 處理的模型可以在更少的 GPU 上運行，而且無需任何額外的代碼優化即可更快地運行：在 24GB 的消費級 GPU 上，作者將 LLAMA-2 70B 的推理總計算量減少到了密集模型的 64%；在 40GB 的 A100 GPU 上，他們將其減少到了 66%。

此外，他們還提出了一種新的概念，即 Transformer 網絡中的計算不變性（computational invariance），它使 SliceGPT 成為可能。

SliceGPT 詳解

SliceGPT 方法依賴于 Transformer 架構中固有的計算不變性。這意味著，你可以對一個組件的輸出應用一個正交變換，只要在下一個組件中撤銷即可。作者觀察到，在網絡區塊之間執行的 RMSNorm 運算不會影響變換：這些運算是可交換的。

在論文中，作者首先介紹了在 RMSNorm 連接的 Transformer 網絡中如何實現不變性，然后說明如何將使用 LayerNorm 連接訓練的網絡轉換為 RMSNorm。接下來，他們介紹了使用主成分分析法（PCA）計算各層變換的方法，從而將區塊間的信號投射到其主成分上。最后，他們介紹了刪除次要主成分如何對應于切掉網絡的行或列。

Transformer 網絡的計算不變性

用 Q 表示正交矩陣：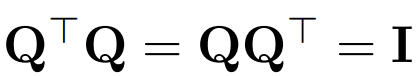

• 注意，向量 x 乘以 Q 不會改變向量的 norm，因為在這項工作中，Q 的維度總是與 transformer D 的嵌入維度相匹配。

假設 X_? 是 transformer 一個區塊的輸出，經過 RMSNorm 處理后，以 RMSNorm (X_?) 的形式輸入到下一個區塊。如果在 RMSNorm 之前插入具有正交矩陣 Q 的線性層，并在 RMSNorm 之后插入 Q^?，那么網絡將保持不變，因為信號矩陣的每一行都要乘以 Q、歸一化并乘以 Q^?。此處有：   

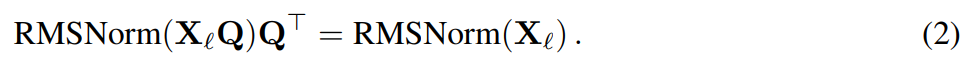
現在，由于網絡中的每個注意力或 FFN 塊都對輸入和輸出進行了線性運算，可以將額外的運算 Q 吸收到模塊的線性層中。由于網絡包含殘差連接，還必須將 Q 應用于所有之前的層（一直到嵌入）和所有后續層（一直到 LM Head）的輸出。

不變函數是指輸入變換不會導致輸出改變的函數。在本文的例子中，可以對 transformer 的權重應用任何正交變換 Q 而不改變結果，因此計算可以在任何變換狀態下進行。作者將此稱為計算不變性，并在下面的定理中加以定義。

定理 1：設 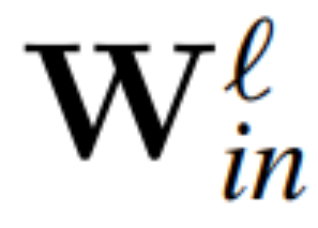和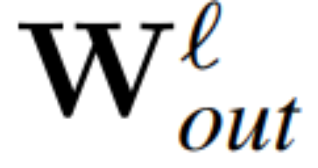為 RMSNorm 連接的 transformer 網絡第 ? 塊線性層的權重矩陣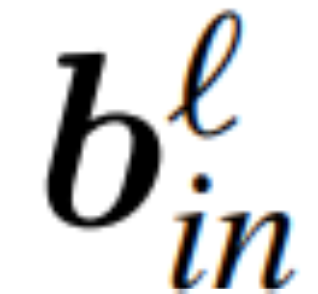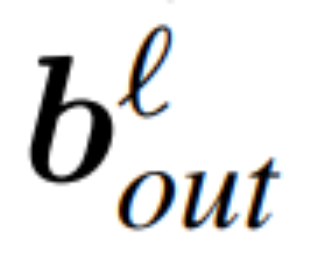，、為相應的偏置（如果有），W_embd 和 W_head 為嵌入矩陣和頭矩陣。設 Q 是維數為 D 的正交矩陣，那么下面的網絡就等同于原來的 transformer 網絡：

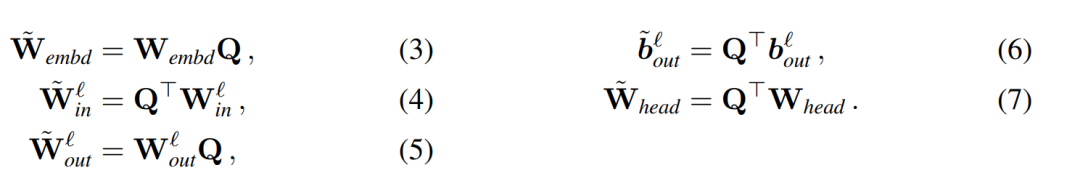
復制輸入偏置和頭偏置：

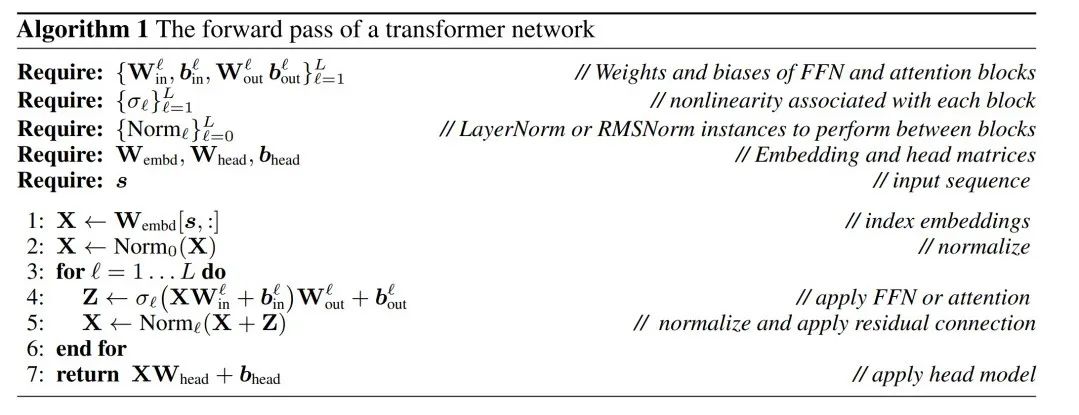
可以通過算法 1 來證明，轉換后的網絡計算出的結果與原始網絡相同。

LayerNorm Transformer 可以轉換為 RMSNorm

Transformer 網絡的計算不變性僅適用于 RMSNorm 連接的網絡。在處理使用 LayerNorm 的網絡之前，作者先將 LayerNorm 的線性塊吸收到相鄰塊中，從而將網絡轉換為 RMSNorm。

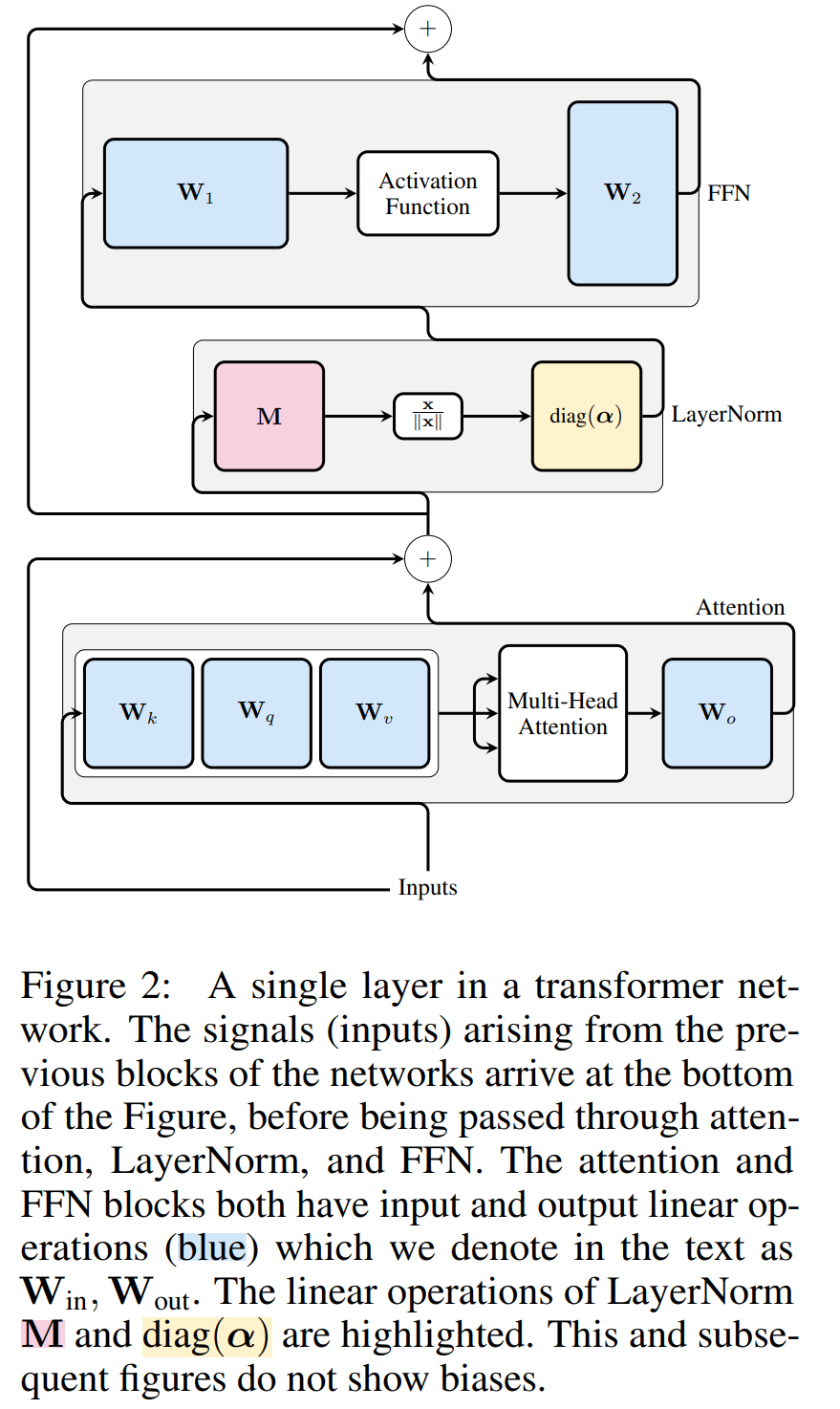
圖 3 顯示了 Transformer 網絡（見圖 2）的這種轉換。在每個區塊中，作者將輸出矩陣 W_out 與均值減法矩陣 M 相乘，后者考慮了后續 LayerNorm 中的均值減法。輸入矩陣 W_in 被前面 LayerNorm 塊的比例預乘。嵌入矩陣 W_embd 必須進行均值減法，而 W_head 必須按照最后一個 LayerNorm 的比例重新縮放。這只是運算順序的簡單改變，不會影響網絡輸出。

每個塊的轉換

現在 transformer 中的每個 LayerNorm 都已轉換為 RMSNorm，可以選擇任意 Q 來修改模型。作者最初的計劃是從模型中收集信號，利用這些信號構建一個正交矩陣，然后刪除部分網絡。他們很快發現，網絡中不同區塊的信號并沒有對齊，因此他們需要在每個區塊應用不同的正交矩陣，即 Q_?。

如果每個區塊使用的正交矩陣不同，則模型不會改變，證明方法與定理 1 相同，但算法 1 第 5 行除外。在這里可以看到，殘差連接和塊的輸出必須具有相同的旋轉。為了解決這個問題，作者通過對殘差進行線性變換 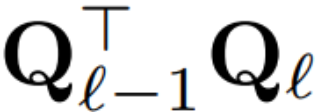  來修改殘差連接。

圖 4 顯示了如何通過對殘差連接進行額外的線性運算，對不同的區塊進行不同的旋轉。與權重矩陣的修改不同，這些附加運算無法預先計算，并且會給模型增加少量（D × D）開銷。盡管如此，還是需要通過這些操作來對模型進行切除操作，而且可以看到整體速度確實加快了。

為了計算矩陣 Q_?，作者使用了 PCA。他們從訓練集中選擇一個校準數據集，在模型中運行（在將 LayerNorm 運算轉換為 RMSNorm 之后），并提取該層的正交矩陣。更確切地說，如果 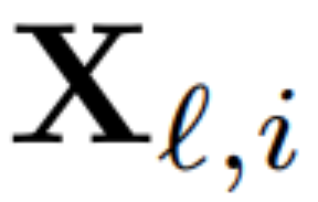 他們使用轉換后網絡的輸出來計算下一層的正交矩陣。更確切地說，如果  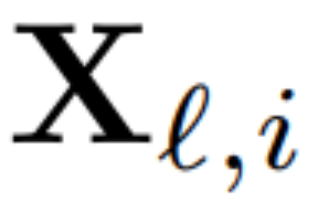是校準數據集中第 i 個序列的第 ? 個 RMSNorm 模塊的輸出，計算：

并將 Q_?設為 C_? 的特征向量，按特征值遞減排序。

切除

主成分分析的目標通常是獲取數據矩陣 X 并計算低維表示 Z 和近似重構：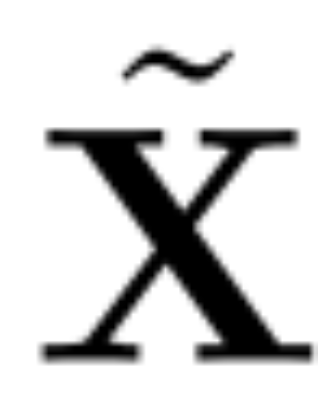

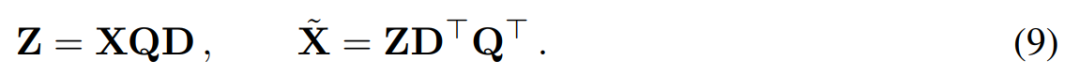
其中 Q 是 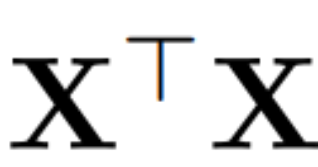 的特征向量，D 是一個 D × D 小刪除矩陣（包含 D × D 同位矩陣的 D 小列），用于刪除矩陣左邊的一些列。從 QD 是最小化  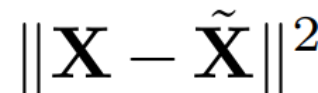的線性映射的意義上來說，重建是 L_2 最佳（L_2 optimal）的。

當對區塊間的信號矩陣 X 應用 PCA 時，作者從未將 N × D 信號矩陣具體化，而是將刪除矩陣 D 應用于構建該矩陣前后的運算。在上述運算中，該矩陣已乘以 Q。作者刪除了 W_in 的行以及 W_out 和 W_embd 的列。他們還刪除了插入到殘差連接中的矩陣 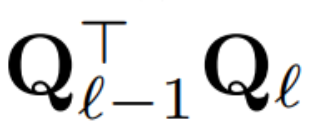 的行和列（見圖 4）。

實驗結果

生成任務

作者對經過 SliceGPT 和 SparseGPT 剪裁后大小不同的 OPT 和 LLAMA-2 模型系列在 WikiText-2 數據集中進行了性能評估。表 1 展示了模型經過不同級別的剪裁后保留的復雜度。相比 LLAMA-2 模型，SliceGPT 在應用于 OPT 模型時表現出了更優越的性能，這與作者根據模型頻譜的分析得出的推測相符。

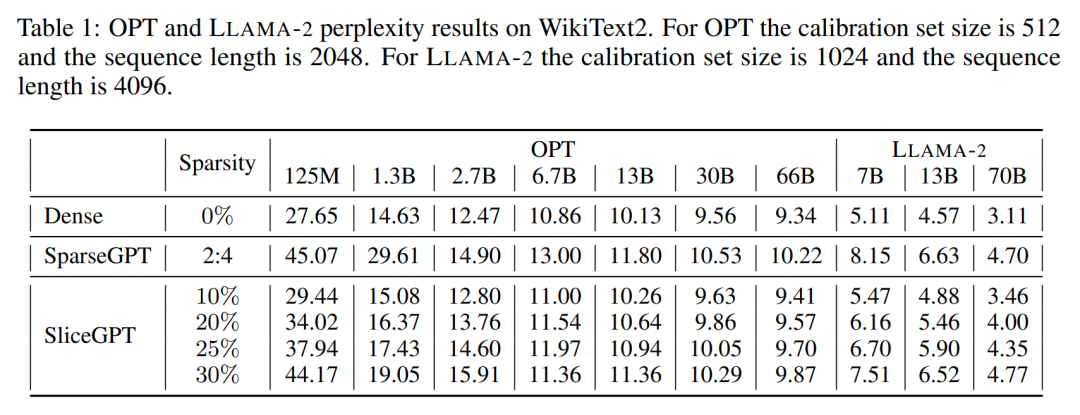
SliceGPT 的性能將隨著模型規模的增大而提升。在對所有 LLAMA-2 系列模型剪裁 25% 情況下，SparseGPT 2:4 模式的表現都遜于 SliceGPT。對于 OPT，可以發現在除 2.7B 模型之外的所有模型中，30% 切除比例的模型的稀疏性都優于 2:4 的稀疏性。

零樣本任務

作者采用了 PIQA、WinoGrande、HellaSwag、ARC-e 和 ARCc 五個任務來評估 SliceGPT 在零樣本任務上的表現，他們在評估中使用了 LM Evaluation Harness 作為默認參數。

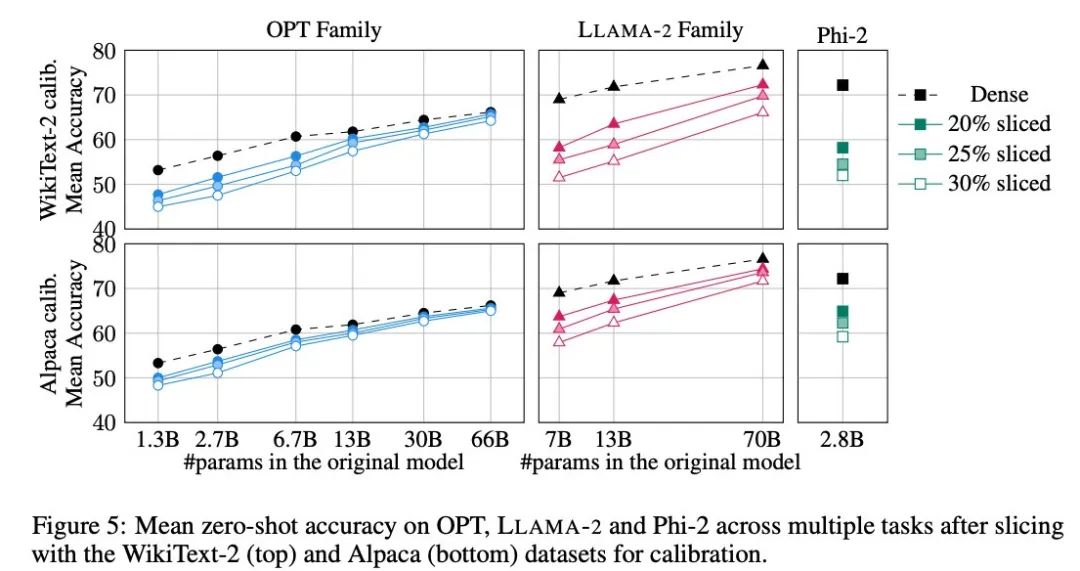
圖 5 展示了經過剪裁的模型在以上任務中取得的平均分數。圖中上行顯示的是 SliceGPT 在 WikiText-2 中的平均準確率，下行顯示的是 SliceGPT 在 Alpaca 的平均準確率。從結果中可以觀察到與生成任務中類似的結論：OPT 模型比 LLAMA-2 模型更適應壓縮，越大的模型經過剪裁后精度的下降越不明顯。

作者在 Phi-2 這樣的小模型中測試了 SliceGPT 的效果。經過剪裁的 Phi-2 模型與經過剪裁的 LLAMA-2 7B 模型表現相當。最大型的 OPT 和 LLAMA-2 模型可以被有效壓縮，當從 66B 的 OPT 模型中刪除 30% 時，SliceGPT 可以做到僅損失了幾個百分點。

作者還進行了恢復微調（RFT）實驗。使用 LoRA 對剪裁過的 LLAMA-2 和 Phi-2 模型進行了少量 RFT。

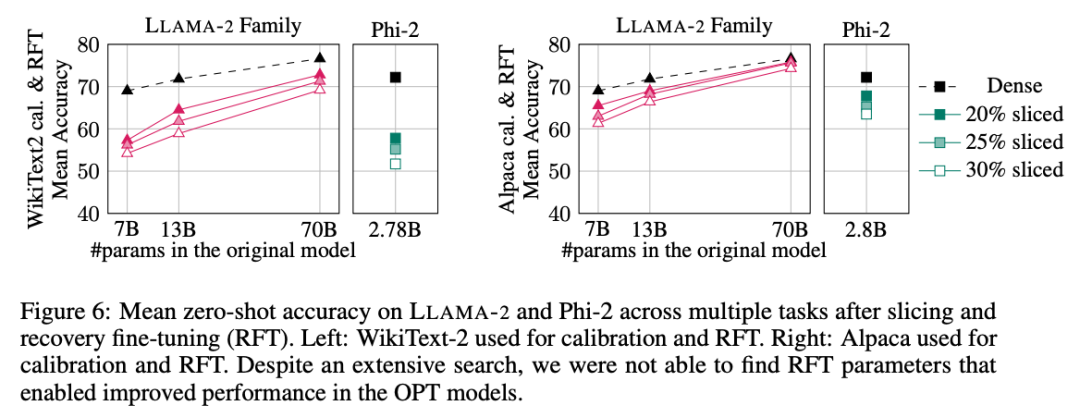
實驗結果如圖 6 所示。可以發現，RFT 的結果在 WikiText-2 和 Alpaca 數據集存在顯著差異，模型在 Alpaca 數據集中展現了更好的性能。作者認為出現差異的原因在于 Alpaca 數據集中的任務和基準任務更接近。

對于規模最大的 LLAMA-2 70B 模型，剪裁 30% 再進行 RFT 后，最終在 Alpaca 數據集中的平均準確率為 74.3%，原稠密模型的準確率為 76.6%。經過剪裁的模型 LLAMA-2 70B 保留了約 51.6B 個參數，其吞吐量得到了顯著提高。

作者還發現 Phi-2 無法在 WikiText-2 數據集中，從被剪裁過的模型中恢復原有準確率，但在 Alpaca 數據集中能恢復幾個百分點的準確率。被剪裁過 25% 并經過 RFT 的 Phi-2 在 Alpaca 數據集中，平均準確率為 65.2%，原稠密模型的準確率為 72.2%。剪裁過的模型保留了 2.2B 個參數，保留了 2.8B 模型準確率的 90.3%。這表明即使是小型語言模型也可以有效剪枝。

基準吞吐量

和傳統剪枝方法不同，SliceGPT 在矩陣 X 中引入了（結構化）稀疏性：整列 X 被切掉，降低了嵌入維度。這種方法既增強了 SliceGPT 壓縮模型的計算復雜性（浮點運算次數），又提高了數據傳輸效率。

在 80GB 的 H100 GPU 上，將序列長度設置為 128，并將序列長度批量翻倍找到最大吞吐量，直到 GPU 內存耗盡或吞吐量下降。作者比較了剪裁過 25% 和 50% 的模型的吞吐量與原稠密模型 80GB 的 H100 GPU 上的吞吐量。剪裁過 25% 的模型最多實現了 1.55 倍的吞吐量提升。

在剪裁掉 50% 的情況下，最大的模型在使用一個 GPU 時，吞吐量實現了 3.13 倍和 1.87 倍的大幅增加。這表明在 GPU 數量固定的情況下，被剪裁過的模型的吞吐量將分別達到原稠密模型的 6.26 倍和 3.75 倍。

經過 50% 的剪裁后，雖然 SliceGPT 在 WikiText2 中的保留的復雜度比 SparseGPT 2:4 差，但吞吐量卻遠超 SparseGPT 的方法。對于大小為 13B 的模型，在內存較少的消費級 GPU 上，小模型的吞吐量可能也會有所提高。

推理時間

作者還研究了使用 SliceGPT 壓縮的模型從端到端的運行時間。表 2 比較了在 Quadro RTX6000 和 A100 GPU 上，OPT 66B 和 LLAMA-2 70B 模型生成單個 token 所需的時間。可以發現，在 RTX6000 GPU 上，對模型剪裁過 25% 后，推理速度提高了 16-17%；在 A100 GPU 上，速度提高了 11-13%。相比原稠密模型，對于 LLAMA-2 70B，使用 RTX6000 GPU 所需的計算量減少了 64%。作者將這種提升歸功于 SliceGPT 采用了用較小的權重矩陣替換原權重矩陣，并使用了 dense kernels ，這是其他剪枝方案無法實現的。

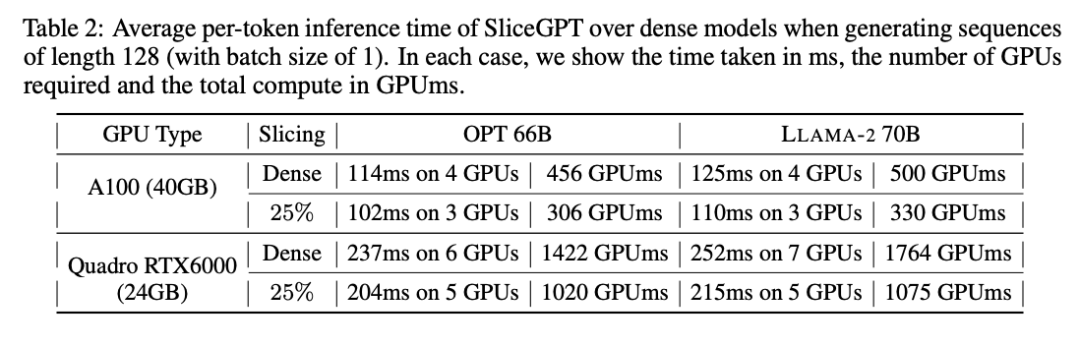
作者表示，在撰寫本文時，他們的基線 SparseGPT 2:4 無法實現端到端的性能提升。相反，他們通過比較 transformer 層中每個運算的相對時間，將 SliceGPT 與 SparseGPT 2:4 進行比較。他們發現，對于大型模型，SliceGPT (25%) 與 SparseGPT (2:4) 在速度提升和困惑度方面具有競爭力。

計算成本 

所有 LLAMA-2、OPT 和 Phi-2 模型都可以在單個 GPU 上花費 1 到 3 小時的時間進行切分。如表 3 所示，通過恢復微調，可以在 1 到 5 個小時內壓縮所有 LM。

了解更多內容，請參考原論文。