AI，的確正在改變數學。

最近，一直十分關注這個議題的陶哲軒，轉發了最近一期的《美國數學學會通報》（Bulletin of the American Mathematical Society）。

圍繞「機器會改變數學嗎？」這個話題，眾多數學家發表了自己的觀點，全程火花四射，內容硬核，精彩紛呈。

作者陣容大咖云集，包括菲爾茲獎得主Akshay Venkatesh、華裔數學家鄭樂雋、紐大計算機科學家Ernest Davis等多位業界知名學者。

要知道，其中很多文章是在一年前提交的，而一年之內，AI的世界已經發生了天翻地覆的變化，其中某些內容可能已經略顯過時了。

然而，盡管如此，這些文章依舊含金量滿滿，甚至讓陶哲軒高呼：這個領域太快了！讓我還沒發表的文章顯得有些多余。

無人可以否認，如今AI工具正在讓數學領域以驚人的速度向前邁進。

人工智能是否將引領包括純數學在內的科學領域，在信息收集和處理方式上的一場革命？它會改變數學研究方法嗎？

對此，數學家們的意見產生了分歧：某些人認為，機器學習在研究中的廣泛應用即將到來，而另一些人則持懷疑態度，他們回顧了1960年代的過度樂觀和隨后的「AI寒冬」。

然而，數學研究實踐中，已經極有可能發生劇變。現在，數學家們是時候考慮這些變化所帶來的問題了。

不用懷疑，風暴就在前方。

那么，機器會改變數學嗎？

數學自動化對數學研究的影響

在這篇論文中，菲爾茲獎得主Akshay Venkatesh探討了自動化對數學研究的影響。

論文地址：https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01834-5/S0273-0979-2024-01834-5.pdf

在這篇論文中，Akshay Venkatesh提出了一個有趣的思想實驗——

2017年，DeepMind的Alphazero一夜之間自學了國際象棋和圍棋，超越了人類。

如果十年后，「Alephzero」（寫作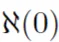），也做了同樣的格式化數學呢？

本文中的「數學」指的是「純數學研究」。

我們的出發點是假設「Alephzero」自學了高中和大學數學，并做完了SpringerVerlag Graduate Terts in Mathematics 系列的所有習題。第二天早上，數學家們將它放出，下載它的孩子們，用我們的計算資源運行它們。

這的確是一個思想實驗，因為它顯然是不現實的：通過把我們的視野限制在未來的十年或二十年，我們允許自己脫離可能伴隨這種技術進步而發生的社會變革來考慮這個問題，也允許我們避免思考更極端的機器智能類型，我們把「Alephzero」當作一個電動工具而不是一個有生命的合作者來建模。

我們可以這樣安慰自己：實際上，這個前提離我們太遙遠了，我們不需要考慮它。但是，如果我們允許哪怕是微乎其微的可能性，這種情況可能會在二十年后發生。

通過數學家和問題網絡中的貝葉斯相互作用，提供了一個非常粗略的模型，展示了我們的部分價值機制。我們現在考慮「Alephzero」將如何影響這個網絡并改變結果。

正如我們所看到的，感知到的困難是我們構建價值的重要組成部分。

無論具體情況如何，「Alephzero」都會改變我們解決問題的能力，從而改變我們對問題難度的看法。

數學過程中可以加速最快的部分將在其感知難度上降低最大，并且根據我們上面的模型，狀態將遭受最大的降低。類似的模式發生在許多自動化實例中。

最后，「Alephzero」將大大擴展數學上有趣問題的整個范圍。它會在專業數學家和其他人之間，創造公平的競爭環境。

機器怎樣讓數學更聚合

論文地址：https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01827-8/S0273-0979-2024-01827-8.pdf

數學家鄭樂雋認為，既然技術已經改變了我們研究數學的方式，那就可以利用這項技術讓數學更具「聚合」，而不是讓人類數學家在面對技術進步時變得多余。

在思考「研究數學」意味著什么時，她研究了數學技術的以下幾個方面：教學和學習、提出問題、協作、傳播和做研究的行為。

這并不是一個嚴謹的分析，而是基于她作為數學家經驗的明智反思。

鄭樂雋認為，雖然現在有一些計算機輔助的校對檢查器，甚至證明生成器，但技術還沒有真正侵占數學研究最深刻、最有創意、最人性化的方面。

深層的創造性部分首先涉及提出想法——定義的想法、證明的想法、在數學的不同部分之間建立聯系的想法、表達事物的新方法的想法、符號和術語的想法、圖解推理的想法以及視覺表示的想法。

為了讓機器做數學研究，我們必須想辦法告訴它們去做，如果我們自己還不知道怎么做，那么我們就很難告訴它們怎么做。

機器可以進行一定程度的證明檢查，但暗地里，數學家們都知道，我們寫不出完全嚴格的證明——我們根據邏輯提出論點，并由我們認為同行能夠填寫的邏輯步驟來支持。

我們沒有定義這些步驟的大小，所以很難告訴機器去做。

生成證明是一種完全不同的技能，而不僅僅是檢查它們，任何數學學生都知道。能夠遵循別人的證據，比自己想出一個新的證據要容易得多。這并不是說計算機在數學研究能力上永遠不可能超過人類數學家。

在她看來，計算機比人類數學家更厲害的地方就在于——

它們有更大的能力來搜索所有可能的動作，通過搜索目前已知的所有可能的邏輯結果，它們就能嘗試提出新的數學。

這需要想象力、猜測和直覺的飛躍，什么足以讓計算機做到這一點？這個想法非常有趣。

計算機能幫我們做邏輯推理嗎

論文地址：https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01833-3/S0273-0979-2024-01833-3.pdf

計算機已經徹底變革了我們進行數學研究的方法，讓復雜的計算變得輕而易舉。

但接下來，它們是否會成為我們邏輯推理的助手？甚至有朝一日，它們能否獨立進行推理呢？

本文將帶你一覽神經網絡、計算機定理證明器以及大語言模型在近期的重要進展。

形式化工具如何幫我們更好地做數學研究

論文地址：https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01832-1/S0273-0979-2024-01832-1.pdf

從20世紀初開始，我們就明白，數學定義和證明能夠通過擁有嚴格語法和規則的形式系統得到表示。

在這一基礎上，計算機證明助手的發展讓我們能夠將數學知識以數字化的形式進行編碼。

本文將探討這類技術及其相關工具如何幫助我們更好地進行數學研究。

用定理證明器，簡化數學研究中的復雜問題

論文地址：https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01831-X/S0273-0979-2024-01831-X.pdf

本文探討了如何利用交互式定理證明器通過設定抽象邊界來簡化數學研究中的復雜問題。

奇異的新宇宙：LLM讓數學家用更自然的語言和證明助手交流

論文地址：https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01830-8/S0273-0979-2024-01830-8.pdf

目前的計算機程序，也就是證明助手，能夠校驗數學證明的正確性，但它們使用的專業證明語言對很多數學家而言構成了一道門檻。

大語言模型（LLM）具有打破這一障礙的可能性，讓數學家們能夠用更自然的語言與證明助手進行交流。這樣不僅能夠培養他們的直覺，還能確保他們的論證過程正確無誤。

用深度學習工具做純數學研究

論文地址：https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01829-1/S0273-0979-2024-01829-1.pdf

本文是關于一位純數學家在研究中嘗試使用深度學習工具時，可能會期待的個人體驗和非正式分享。

AI能做數學研究嗎

論文地址：https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01828-X/S0273-0979-2024-01828-X.pdf

本文探討了目前AI技術在解決融合了基礎數學和常識推理的文字題目方面的能力和局限。

作者回顧了三種利用AI自然語言技術開發的方法：直接給出答案、生成解題的計算機程序，以及生成可供自動定理驗證器使用的形式化表述。

作者認為，這些限制在發展純數學研究用的AI技術中的重要性尚未明確，但它們在數學應用中極為關鍵，并且在開發能夠理解人類編寫的數學內容的程序時也很重要。

機器時代下的證明是怎樣的

論文地址：https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01826-6/S0273-0979-2024-01826-6.pdf

作者在本文中探討了證明的本質及其在機器時代的演變，并通過對比傳統驗證和計算機驗證中的價值觀進行了分析。

文章最終提出的方法可能使計算機證明借鑒人類經驗中的成功策略。

自動化，讓數學家反思自己的價值

論文地址：https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01825-4/S0273-0979-2024-01825-4.pdf

在這篇論文中，作者嚴厲地批評了同行們缺乏思考，尤其是在考慮數學的機械化未來時，他們忽視了社會更廣泛層面上關于技術和人工智能的重要辯論。

p-adic數域中的連分數

論文地址：https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01819-9/S0273-0979-2024-01819-9.pdf

連分數在數論特別是丟番圖逼近這一領域享有悠久的歷史。

本文旨在概述p-adic連分數理論的核心成果，這是一種定義在p-adic數域Qp上的連分數。

內容將從基本概念講起，直至介紹最新進展和當前面臨的開放性問題。

陶哲軒發文：機器輔助證明

順便，陶哲軒也安利了一下自己之前寫的論文「Machine assisted proof」。

論文地址：https://terrytao.files.wordpress.com/2024/03/machine-assisted-proof-notices.pdf

在這篇論文中陶哲軒表示，借助于LLM處理自然語言輸入的能力，它們很可能成為一個用戶友好的平臺，使得那些不具備特定軟件知識的數學家也能夠使用高級工具。

如今，他和很多科學家已經習慣使用這些模型來生成各種語言的簡單代碼，包括符號代數包，或者制作復雜的圖表和圖像了。

目前，由于形式化證明驗證（formal proof verification）工作非常依賴人力，這使得實時將大量當前研究論文完全形式化變得不切實際。

在偏微分方程領域中，常常需要通過多頁的計算來估計涉及一個或多個未知函數（比如PDE的解）的積分表達式。

其中便涉及到使用這些函數在不同函數空間范數（如Sobolev空間范數）中的界限，結合標準不等式（例如H?lder不等式和Sobolev不等式），以及諸如分部積分或積分符號下的微分等恒等式。

這類計算雖然是常規操作，但可能包含各種程度的錯誤（如符號錯誤），對審稿人來說，細致地檢查這些計算既枯燥又費時，而且這些計算本身除了最終的估計結果是正確的之外，很難提供更深入的數學理解或見解。

可以設想，未來可能開發出工具，以自動或半自動的方式建立數學估計，并且將目前那些既冗長又缺乏啟發性的估計證明替換為一個指向形式證明證書的鏈接。

更進一步，我們也許能夠期待，基于一組初始的假設和方法，未來的AI工具能夠提出它所能得出的最佳估計，而無需先進行紙筆計算來預測這個估計可能是什么。

目前來看，估計可能的狀態空間過于復雜，難以自動化地進行探索；但隨著技術的發展，實現這種自動化探索的可能性并非遙不可及。

一旦實現，我們就能在目前看來不可行的規模上進行數學探索。

還是以偏微分方程為例，目前的研究通常一次只研究一到兩個方程；但在未來，我們可能能同時研究數百個方程。

例如，先對一個方程完整地展開論證，然后讓AI工具將這些論證調整適用于大量相關的方程族，必要時，當論證的擴展出現非常規情況時，AI會向作者提問。

如今，在數學的其他領域，比如圖論，這種大規模數學探索的初步跡象已經開始顯現。

但目前的這些初步嘗試，由于依賴于計算量極大的AI模型或需要大量的專家級人工參與和監督，因此難以大規模推廣。

然而，陶哲軒相信在不遠的將來，我們將見證更多創新的機器輔助數學方法的誕生。