就在剛剛，MIT物理學家用AI發現了物理學中的新方程。

論文地址：https://arxiv.org/abs/2405.04484

作者表示：這篇論文并沒有解決價值數百萬美元的核聚變問題，而是在更簡單的設置中，引入一個有前途的概念驗證。

偏微分方程（PDE），可以說是物理學家的面包和黃油，但它們非常罕見，人類科學家很難只用紙筆就能發現。

為此，研究者們推出了一個名為OptPDE的AI系統。

使用這個AI，就可以發現新的、從未見過的可積偏微分方程！

具體來說，使用了5000個隨機初始化的PDE系數值運行OptPDE后，研究者發現了4個可積偏微分方程，其中是一個是已知的，而另外三個是全新的方程。

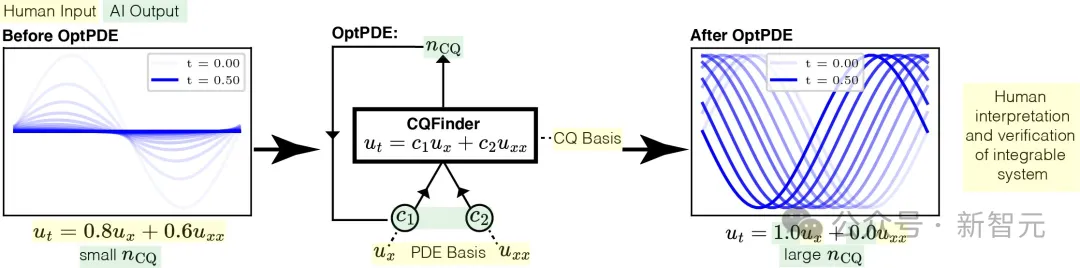
利用這種首創的機器學習方法，MIT的科學家們為物理學提供了一種全新的研究模式。

從此，可以由人類向系統提供領域知識，AI產生希望的假設，然后再由人類進行解釋和驗證。

這就實現了整個物理學發現的閉環。

網友：AI將顛覆各個科學領域

對于這項研究，網友們紛紛表示震撼。

「太燒腦了！如果我正確理解了他們的意思，那這個AI實在是強大到可怕！能夠按需生成模型庫來模擬物理系統，是非常巧妙的技巧，讓我們可以從AI驅動的解決中，節省大量計算。」

「即便只在這些層面上，我們擁有的AI也能為各種科學領域提供新的見解和想法，它們會變得更好！」

「我只是點開看看是不是Max Tegmark大牛的研究，果然如此。」

這位網友則給出了更為專業的解釋——

從本質上講，他們是對偏微分方程應用了獎勵函數，因為偏微分方程具有較多的CQs，并且自然系統遵循定律（例如熱力學）。

由于發現這些偏微分方程往往非常困難，因此這項工作很有意義，因為它提供了一條將加速計算的計算杠桿應用于任務的途徑。

這為生成類似OEIS（整數序列在線百科全書）的資源提供了機會。這就允許來自任何領域的研究搜索這些數據庫，看看以前是否已經解決了類似的問題，或者相關的序列或結構是否已經存在，而不需要從頭開始。

快速「入門」

當PDE具有守恒量時，它們是可積的（例如，能量是質量彈簧的一個守恒量）。

因此，研究者將OptPDE設計為一個兩部分的系統，它可以——

（1）計算任何PDE的守恒量（CQ）數量；

（2）找出使n_CQ最大化的偏微分方程。

下面是（1）在一些熟悉的系統中的實際應用。

因為研究者尋找n_CQ的方法是可微分的，因此要發現新的可積偏微分方程，只需使PDE中的項系數可訓練，并通過SGD最大化n_CQ即可。

他們以從u_x => u_xxx^3的項為基礎，運行了5000次。

下面是解決方案的3D PCA——

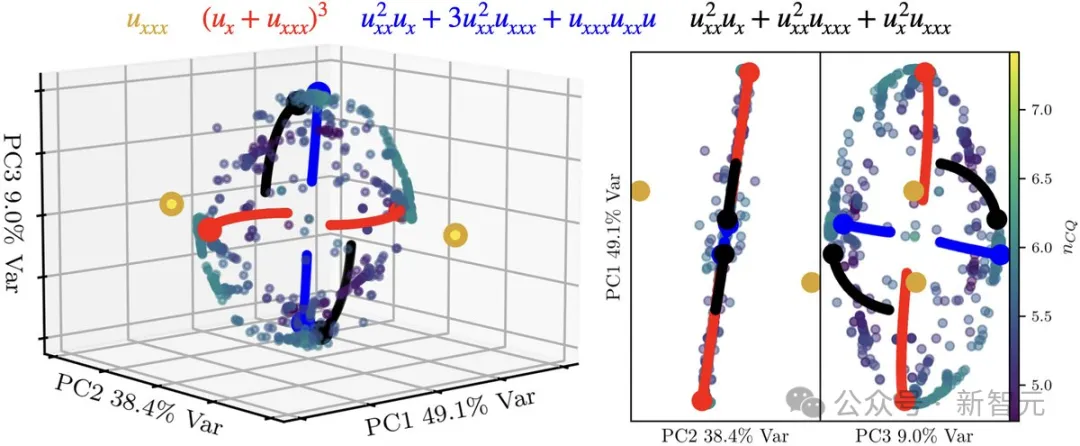
研究者發現，他們得到大多數解，都是4個偏微分方程家族的線性組合，其中一個是KdV方程的一種形式，還有3個方程完全是新增的，在文獻中并沒有記載！

由此，研究者確認，這些新出現的可積偏微分方程中，至少具有一個守恒量。

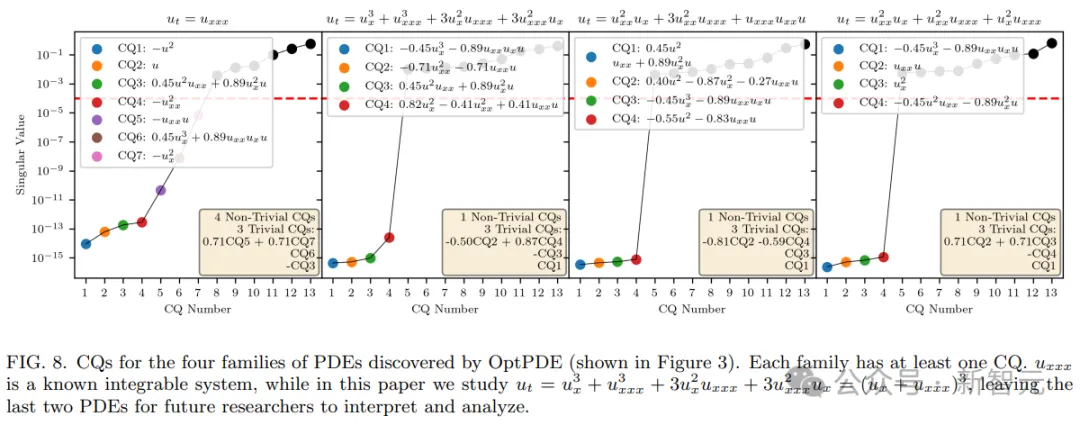
也就是，在AI的幫助下，人類科學家發現了一些全新的可積偏微分方程！

不過，如果想解釋和分析這些發現，還是要靠人類科學家。

研究者仔細分析了以下紅色偏微分方程的簡化版本（u_t=u_x^3），發現它表現出斷裂、無限的CQ，而冪律衰減為了三角波。

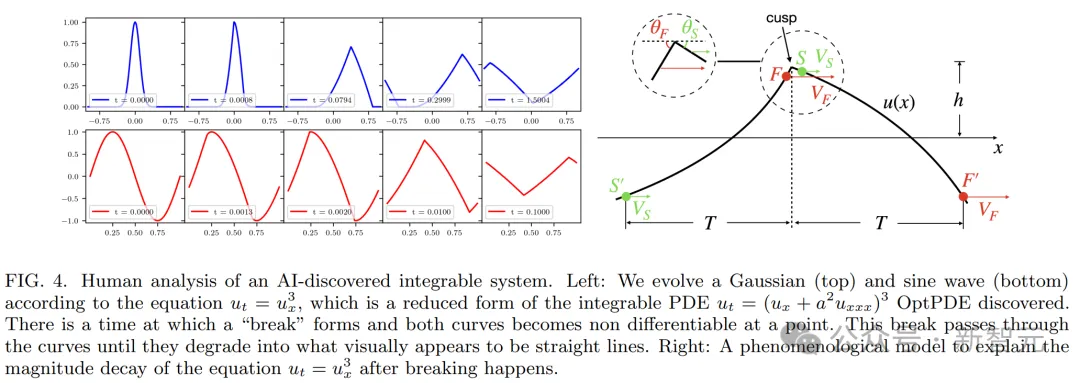
從此，物理學家非常有希望使用OptPDE，來發現更多新穎的可積偏微分方程，來模擬物理學中的復雜現象。

不過，OptPDE要求AI和人類科學家協同工作，作者呼吁：如果這種范式能被物理學界接受，物理學家很可能用現代AI工具做出以前更多新發現。

可積系統：極其罕見，難以發現

可積系統在物理學和工程系中發揮著重要作用，因為易于處理、可預測、可控。

然而，它們極其罕見，難以發現。

傳統中發現可積系統的方法是靠紙筆，它側重于符號推到，還需要考慮到可能系統和守恒量（CQ）的指數級大搜索空間，效率極低。

由此，MIT的物理學家想到：AI可以做什么嗎？

為此，他們引入了一個可積系統發現解決方案OptPDE。

此前，已經有許多工作使用極其學習從物理數據和微分方程中發現守恒量，但MIT研究者的方法，對于偏微分方程來說是最可解釋的。

更重要的是，此前的方法并不能主動優化和設計偏微分方程。

然而，這個AI可以做到！

雖然過去機器學習方法已經被用來發現守恒量，但這項工作第一次提出——

通過驗證和解釋可集成系統，AI和人類科學家可以協同工作。

論文方法

研究者是通過以下階段構建這個方法的。

1.CQFinder——查找PDE的守恒量。

2.OptPDE——使用CQFinder中的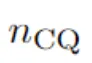，來發現可積PDE。

圖1說明了整個流程。不過需要注意的是，這個流程需要人類科學家通過輸入CQ和PDE基礎，和AI協同工作，這就需要對該領域知識的掌握。

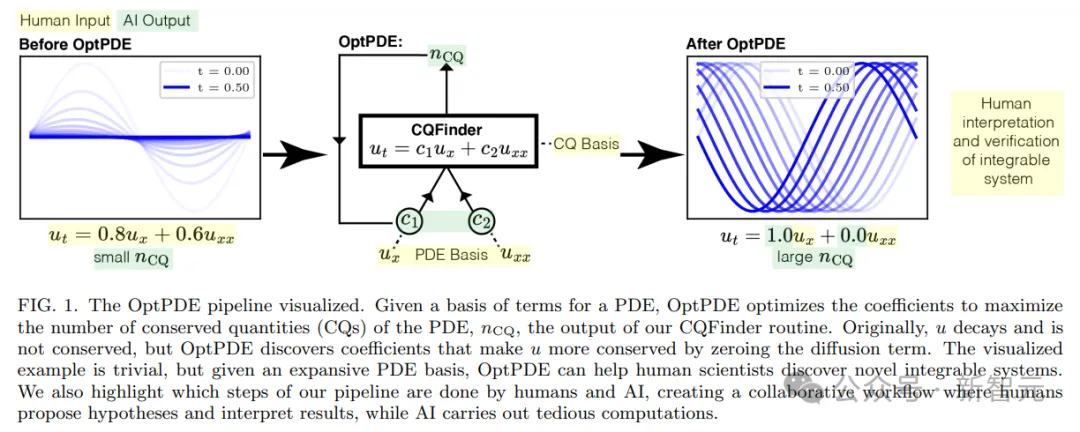
OptPDE的可視化管線。給定PDE的項基礎，OptPDE就會優化系數，從而最大化PDE的守恒量(CQ) 數量。起初，u會衰減并且不守恒，但OptPDE會通過將擴散項歸零，來發現使u更加守恒的系數。這個可視化示例很簡單，但鑒于廣泛的PDE基礎，OptPDE可以幫助人類科學家發現新穎的可積系統

為了構建OptPDE，必須首先設計CQFinder，來準確計算任何PDE的CQ。

具體來說，需要一個具有空間變量x的時間一階偏微分方程，其形式為。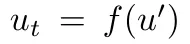

其中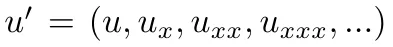，是u及其空間導數的集合，且具有自由邊界條件。

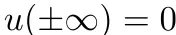研究者需要考慮形式為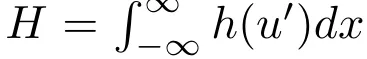的守恒量。

對于一個CQ量，它必須在u的整個時間演化過程中保持恒定。

可以將CQ的時間不變性表示為：

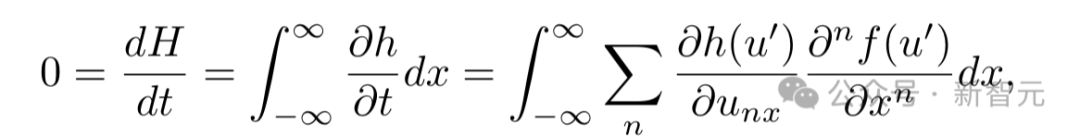
其中，。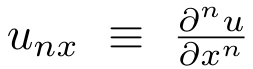

雖然這個方程看起來很復雜，但只要考慮一個簡單的設定就可以了，其中h(u′) 是k個預定義基函數的線性組合，即。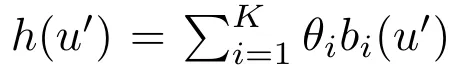

在這里，研究者需要處理兩個無窮大。

1. 理論上，線性方程對于任何光滑的u都必須成立；在實踐中，就可以測試方程是否可以近似這個無限的函數集。

2. 理論上積分是在(-∞,∞)上進行的；在實踐中，就需要用有限范圍來近似它(在范圍之外將u強制為零)。

研究者希望，在CQFinder中創建子流程，從而進行稀疏化和識別簡單解決方案，因為它們更容易被人類科學家解釋。

具體來說，研究者需要將PDE參數化為預定義PDE的線性組合，。

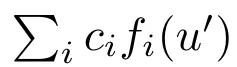CQFinder采用固定的PDE，并輸出其守恒量的數量。

由于CQFinder是用PyTorch編寫的，因此它原則上是可微分的，因此，研究者就可以通過自動微分，來識別PDE系數中的哪些擾動會增加CQ。

然而，可微性的最大挑戰是守恒量本質上是離散的（比如，偏微分方程可以具有3或4個守恒量，而非3.7個）。

為了反向傳播優化系數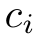， 目標函數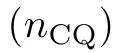就必須是可微的。

為了解決這個問題，研究者使用sigmoid函數引入了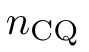的平滑版本。

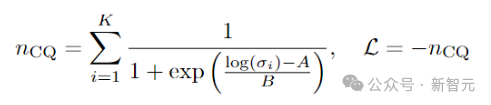
論文結果

CQFinder基準測試

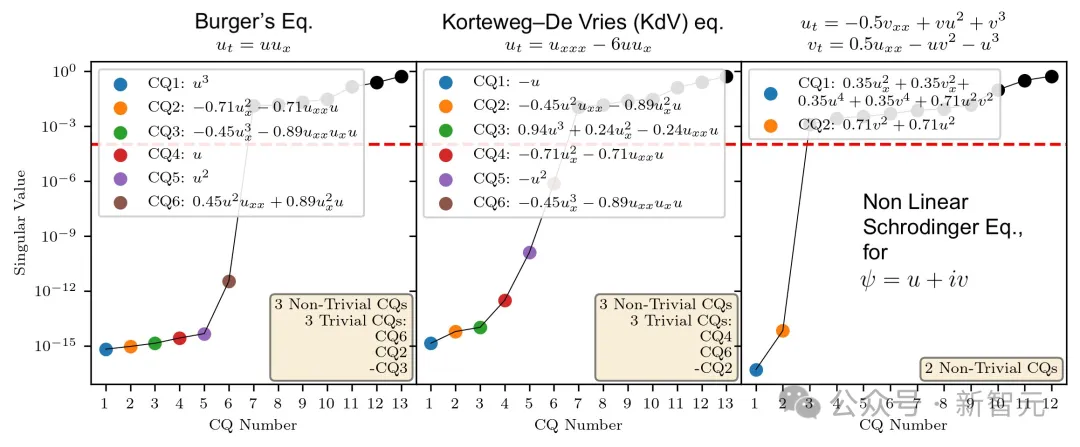
為了驗證CQFinder是否如大家設想的那樣可以工作，研究者在Burgers、Korteweg-DeVries(Kd)和薛定諤方程三個測試系統上運行了它。

圖2顯示，奇異值曲線顯示出從小到大的急劇相變，從而可以清楚地區分消失值和非消失值。

這就證明了，CQFinder不僅可以正確計算守恒量的數量，而且還可以獲得它們的符號公式。

AI發現了三種新穎的可積系統

研究者發現，通過使用Opt-PDE最大化守恒量，來定位OptPDE的流形，就可以發現全新的可積系統。

一般選擇PDE為單個方程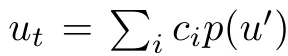，其中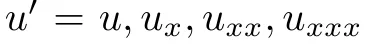，p是最多3次的多項式。

在實踐中，研究者對系數使用廣義球坐標，自然地強制歸一化。

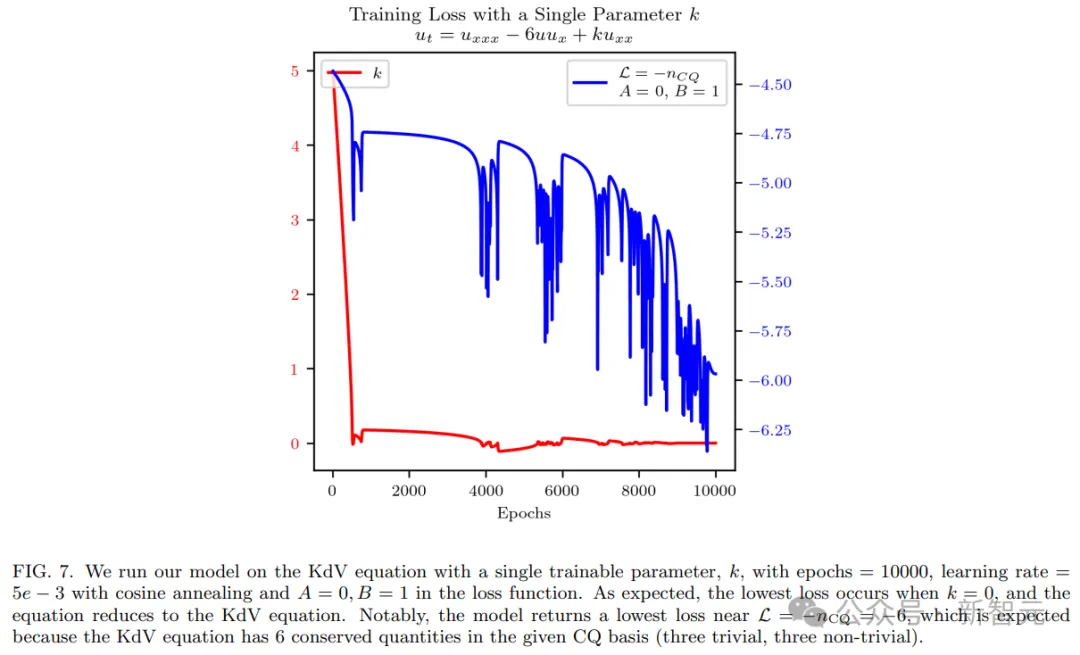
在OptPDE中，研究者使用A=0，B=1000，epochs=25000，學習率為10^-3，余弦退火，Tmax=5000。

研究者運行OptPDE，為其余33個參數隨機選擇5000個初始化位置。

然后，研究者使用3D PCA可視化返回的參數值，來分析OptPDE的結果，如圖3所示。

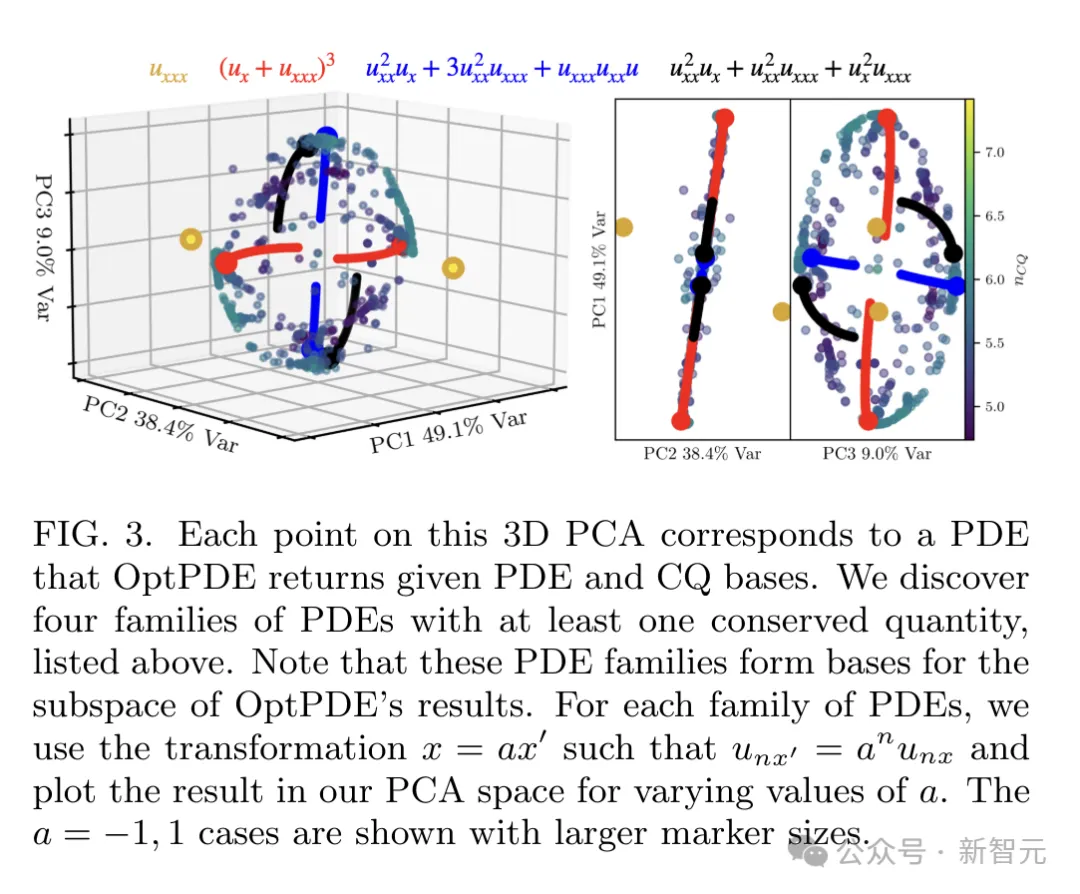
可以看到，解的流形結構非常有趣：兩側有兩個極點，環狀的解位于中間。

兩個極點代表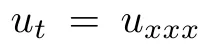，它是可積KdV方程的簡化形式，而環狀的解就更為復雜了。

在這些環狀的解中，研究者進行了插值。

然后，他們找到了作為環狀子空間基礎的三個偏微分方程組，如圖3所示。

守恒量可以顯示出，這三個偏微分方程中的每一個都是新的，且本質上都是有趣的。（如附錄I所示）

研究者將重點放在了下面這個偏微分方程上，因為它的形式很緊湊——

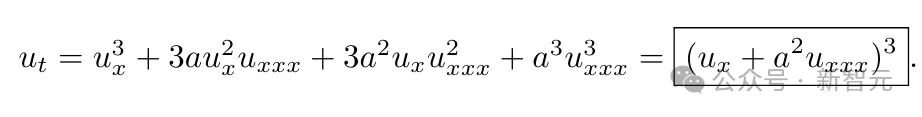
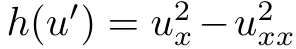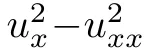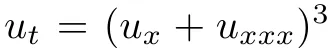研究者在該方程的a=1情況下，運行了CQFinder，發現它有一個非平凡的CQ——經過一系列冗長的代數操作，研究者從數值和符號上驗證了，確實是的CQ。

到這里，研究者可以確信：OptPDE發現了一個新的偏微分方程家族，它們承認有趣的守恒量——。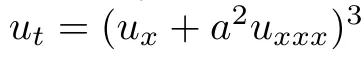

人類責任：對AI的發現進行解釋

而到這里，MIT的研究者們表示，接下來人類就要扛起責任了！

人類科學家需要做的，就是采用AI發現的偏微分方程家族，并對其進行解釋。

在論文中，研究者僅限于分析a?1的情況，使得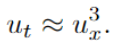

這種特殊情況代表了一個真正的可積系統，并且具有無限數量的CQ。也即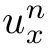對于所有n都是守恒的。

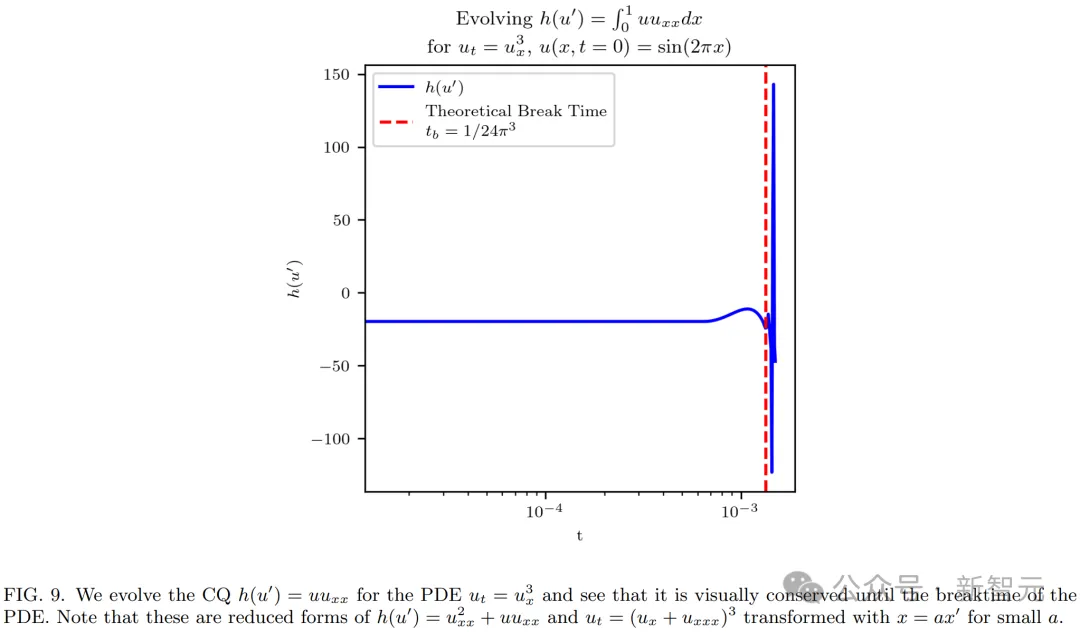
在Mathematica中，研究者繪制了具有高斯和正弦初始條件的偏微分方程的演化，如下圖所示。

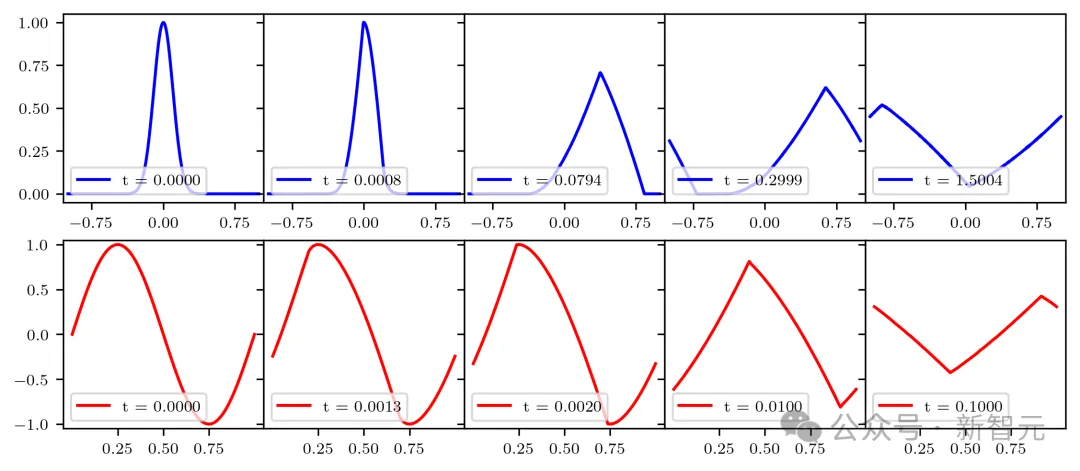
從視覺上看，演化似乎是一種波，在break time后就退化為了一種線性分量，此時，波在某一點就變得不可微分。

研究者推導了break time的符號形式，并為方程式在break time后的行為，創建了一個現象學模型。

Break Time

研究者注意到，通過對x的兩邊進行積分，可以使公式4類似于Burgers公式。

利用特征方程，就可以追蹤出恒定u的路徑，并找到兩個特征相交的最早時間。

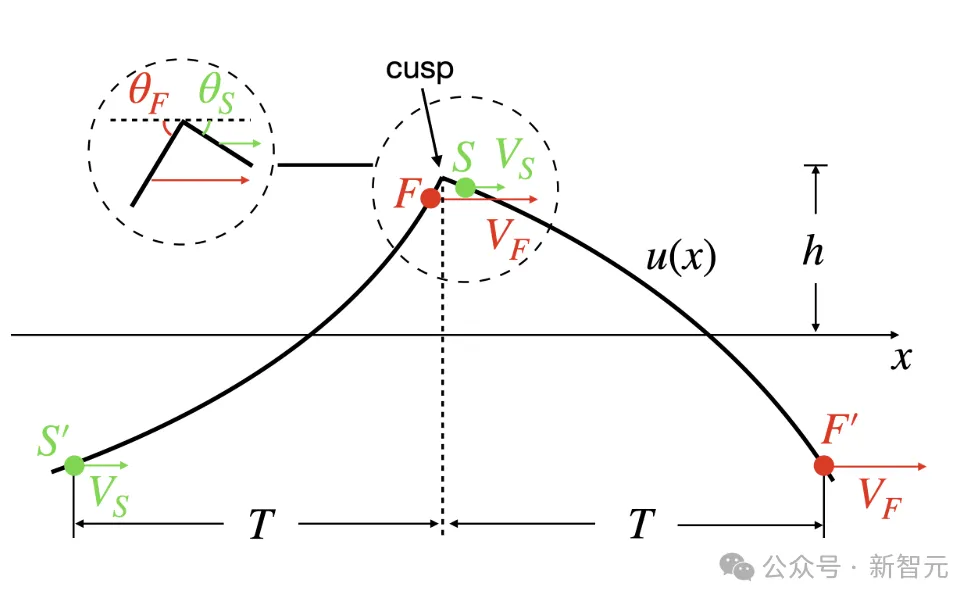
最終可以得出，Break Time為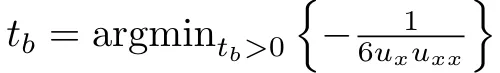，這與研究者在附錄L中的模擬結果大致吻合。

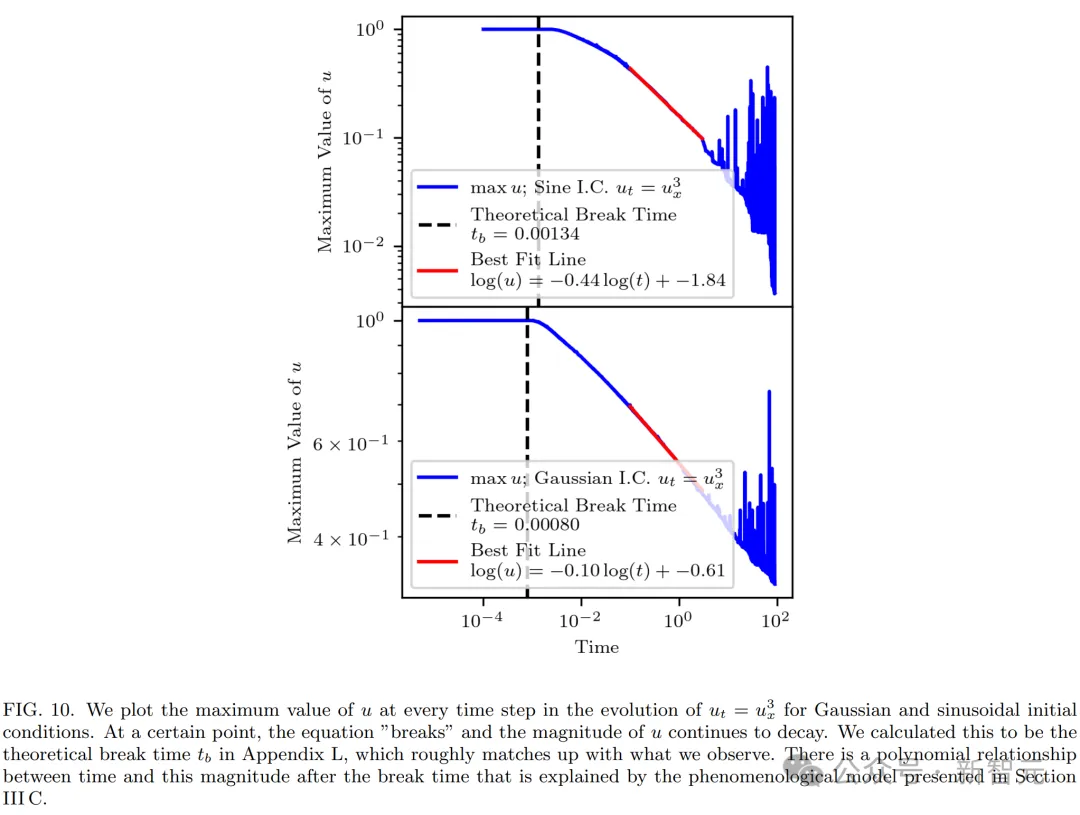
現象學模型

為了理解波break后的行為，研究者希望建立一個現象學模型，來解釋波接近三角波時的動態。

對此，研究者進行了以下推導。

其中一個特殊情況就是a=1，當曲線沿高度均勻收縮時，就得到了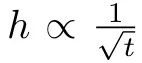，這就和正弦波的情況相吻合。

對其他解的物理理解

從圖3可以看出，研究者所得到的解是高階和非線性的，其立方項由三階導數組成。

要運用物理學的直覺來處理這些問題，可能會令人生畏，但研究者注意到，三階導數出現了在 KdV方程中，或者說，如果推導出具有穩定度和其他阻力的弦的波動方程，也會出現三階導數。

非線性多項式方程在物理學中并不多見，但確實存在，比如高速運動時的空氣阻力公式。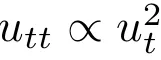

因此，復雜微分方程在物理現象建模中，是非常有用的。

至于其他結果，研究者表示，希望其他科學家也參與進來共同解釋它們。

總之，通過MIT研究者引入的這種人類科學家和AI協作的范式，很可能激勵人類物理學家為物理學做出新的發現！

作者介紹

Subhash Kantamneni

Subhash Kantamneni目前在MIT攻讀物理和計算機科學本科。

他在研究實驗室、高科技創業公司以及對沖基金等多樣化的工作環境中積累了豐富經驗。