對基礎模型進行 scaling 是指使用更多數據、計算和參數進行預訓練，簡單來說就是「規模擴展」。

雖然直接擴展模型規模看起來簡單粗暴，但也確實為機器學習社區帶來了不少表現卓越的模型。之前不少研究都認可擴大神經模型規模的做法，所謂量變引起質變，這種觀點也被稱為神經擴展律（neural scaling laws）。

近段時間，又有不少人認為「數據」才是那些當前最佳的閉源模型的關鍵，不管是 LLM、VLM 還是擴散模型。隨著數據質量的重要性得到認可，已經涌現出了不少旨在提升數據質量的研究：要么是從大型語料庫中過濾出高質量數據，要么是生成高質量的新數據。但是，過去的擴展律一般是將「數據」視為一個同質實體，并未將近期人們關注的「數據質量」作為一個考量維度。

盡管網絡上的數據規模龐大，但高質量數據（基于多個評估指標）通常很有限。現在，開創性的研究來了 —— 數據過濾維度上的擴展律！它來自卡內基梅隆大學和 Bosch Center for AI，其中尤其關注了「大規模」與「高質量」之間的數量 - 質量權衡（QQT）。

• 論文標題：Scaling Laws for Data Filtering—Data Curation cannot be Compute Agnostic
• 論文地址：https://arxiv.org/pdf/2404.07177.pdf
• 代碼地址：https://github.com/locuslab/scaling_laws_data_filtering

如圖 1 所示，當訓練多個 epoch 時，高質量數據的效用（utility）就不大了（因為模型已經完成了學習）。

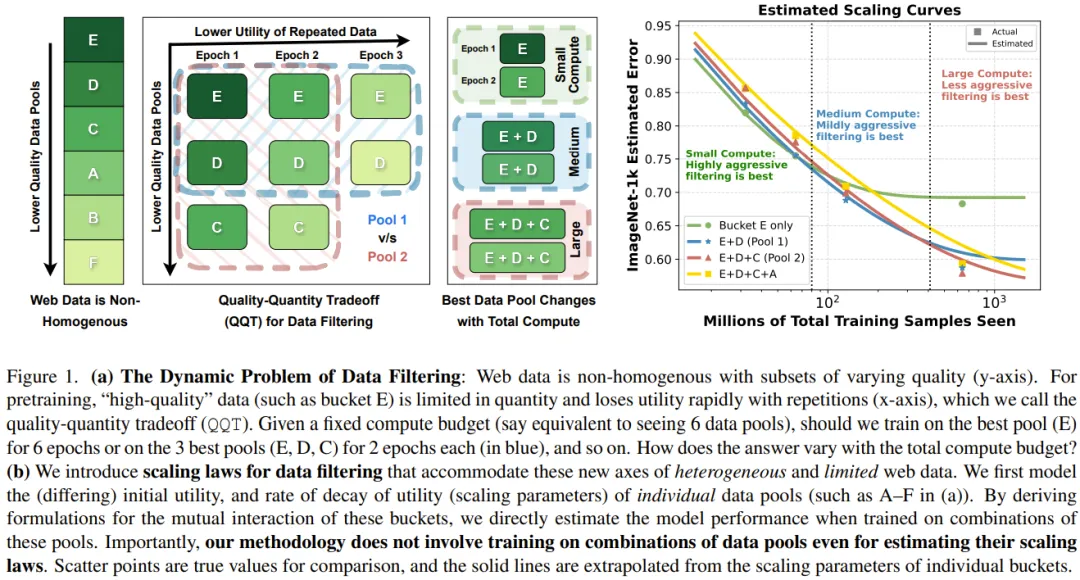
此時，使用更低質量的數據（一開始的效用更小）往往比重復使用高質量數據更有助益。

在數量 - 質量權衡（QQT）之下，我們該如何確定訓練使用怎樣的數據搭配更好？

為了解答這個問題，任何數據整編（data curation）工作流程都必須考慮模型訓練所用的總計算量。這不同于社區對數據過濾（data filtering）的看法。舉個例子，LAION 過濾策略是從常見爬取結果中提取出質量最高的 10%。

但從圖 2 可以看出，很明顯一旦訓練超過 35 epoch，在完全未整編的數據集上訓練的效果優于在使用 LAION 策略整編的高質量數據上訓練的效果。

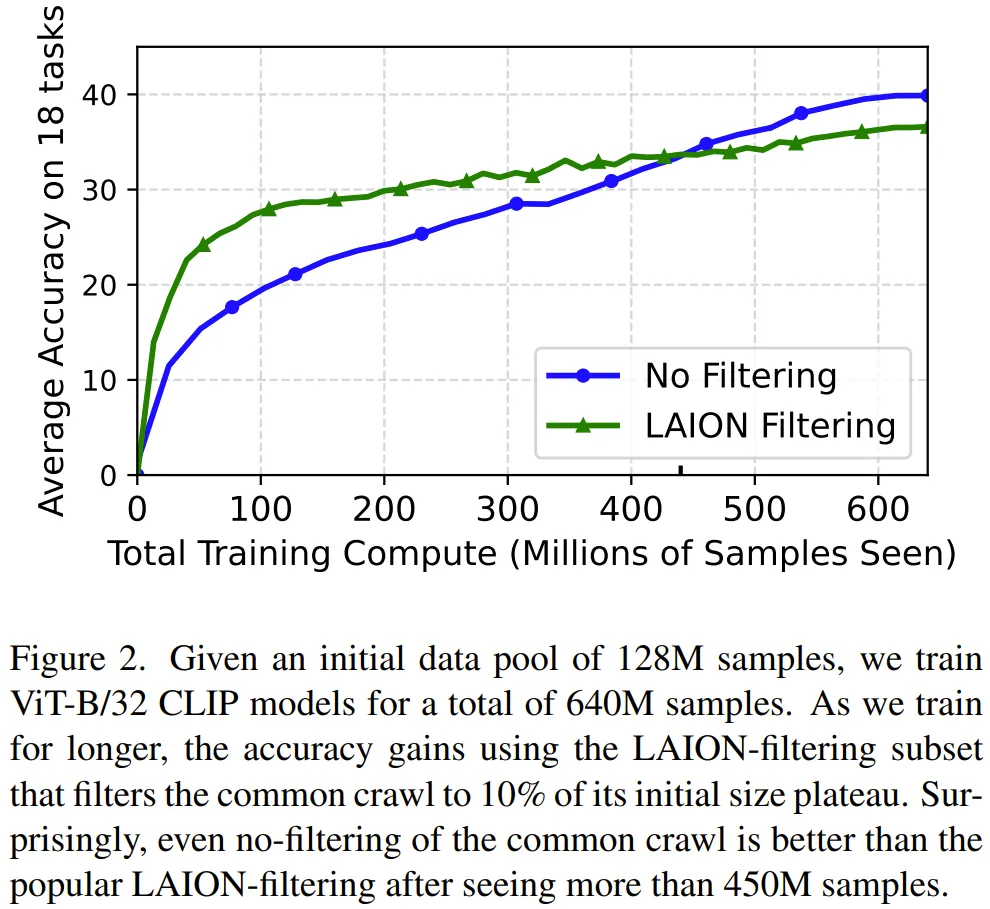
當前的神經擴展律無法建模質量與數量之間這種動態的權衡。此外，視覺 - 語言模型的擴展律研究甚至還要更加更少，目前的大多數研究都僅限于語言建模領域。

今天我們要介紹的這項開創性研究攻克了之前的神經擴展律的三大重要局限，其做到了：

（1）在擴展數據時考慮「質量」這個軸；

（2）估計數據池組合的擴展律（而無需真正在該組合上進行訓練），這有助于引導實現最優的數據整編決策；

（3）調整 LLM 擴展律，使之適用于對比訓練（如 CLIP），其中每一批都有平方數量的比較次數。

該團隊首次針對異構和數量有限的網絡數據提出了擴展律。

大型模型是在多種質量的數據池組合上訓練完成的。通過對從各個數據池的擴散參數（如圖 1 (a) 中的 A-F）派生的聚合數據效用進行建模，就可以直接估計模型在這些數據池的任意組合上的性能。

需要重點指出，這種方法并不需要在這些數據池組合上進行訓練就能估計它們的擴展律，而是可以根據各個組成池的擴展參數直接估計它們的擴展曲線。

相比于過去的擴展律，這里的擴展律有一些重要差異，可以建模對比訓練機制中的重復，實現 O (n2) 比較。舉個例子，如果訓練池的大小倍增，對模型損失有影響的比較次數就會變成原來的四倍。

他們用數學形式描述了來自不同池的數據的相互交互方式，從而可以在不同的數據組合下估計模型的性能。這樣便可以得到適合當前可用計算的數據整編策略。

這項研究給出的一個關鍵信息是：數據整編不能脫離計算進行。

當計算預算少時（更少重復），在 QQT 權衡下質量優先，如圖 1 中低計算量下的激進過濾（E）的最佳性能所示。

另一方面，當計算規模遠超過所用訓練數據時，有限高質量數據的效用會下降，就需要想辦法彌補這一點。這會得到不那么激進的過濾策略，即數據量更大時性能更好。

該團隊進行了實驗論證，結果表明這個用于異構網絡數據的新擴展律能夠使用 DataComp 的中等規模池（128M 樣本）預測從 32M 到 640M 的各種計算預算下的帕累托最優過濾策略。

一定計算預算下的數據過濾

該團隊通過實驗研究了不同計算預算下數據過濾的效果。

他們使用一個大型初始數據池訓練了一個 VLM。至于基礎的未過濾數據池，他們選用了近期的數據整編基準 Datacomp 的「中等」規模版本。該數據池包含 128M 樣本。他們使用了 18 個不同的下游任務，評估的是模型的零樣本性能。

他們首先研究了用于獲得 LAION 數據集的 LAION 過濾策略，結果見圖 2。他們觀察到了以下結果：

1. 在計算預算低時，使用高質量數據更好。

2. 當計算預算高時，數據過濾會造成妨害。

原因為何？

LAION 過濾會保留數據中大約 10% 的數據，因此計算預算大約為 450M，來自已過濾 LAION 池的每個樣本會被使用大約 32 次。這里的關鍵見解是：對于同一個樣本，如果其在訓練過程中被多次看見，那么每一次所帶來的效用就會下降。

之后該團隊又研究了其它兩種數據過濾方法：

（1）CLIP 分數過濾，使用了 CLIP L/14 模型；

（2）T-MARS，在掩蔽了圖像中的文本特征（OCR）后基于 CLIP 分數對數據進行排名。對于每種數據過濾方法，他們采用了四個過濾層級和多種不同的總計算量。

圖 3 給出了在計算規模為 32M、128M、640M 時 Top 10-20%、 Top 30%、Top 40% CLIP 過濾的結果比較。

在 32M 計算規模時，高度激進的過濾策略（根據 CLIP 分數僅保留前 10-20%）得到的結果最好，而最不激進的保留前 40% 的過濾方法表現最差。但是，當計算規模擴展到 640M 時，這個趨勢就完全反過來了。使用 T-MARS 評分指標也能觀察類似的趨勢。

數據過濾的擴展律

該團隊首先用數學方式定義了效用（utility）。

他們的做法不是估計 n 的樣本在訓練結束時的損失，而是考慮一個樣本在訓練階段的任意時間點的瞬時效用。其數學公式為：

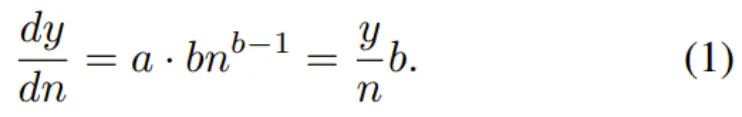
這表明，一個樣本的瞬時效用正比于當前損失且反比于目前所見到的樣本數量。這也符合我們的直觀想法：當模型看到的樣本數量變多，樣本的效用就會下降。其中的重點是數據效用參數 b 。

接下來是數據被重復使用之下的效用。

數學上，一個被見到 k+1 次的樣本的效用參數 b 的定義為：

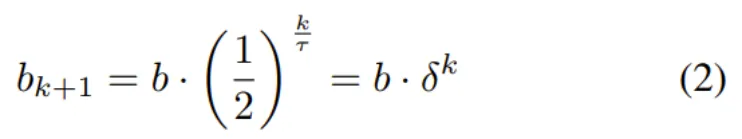
其中 τ 是效用參數的半衰期。τ 值越高，樣本效用隨著重復而衰減得越慢。δ 則是效用隨重復的衰減情況的簡潔寫法。那么，模型在看過 n 個樣本且每個樣本都被看過 k 次之后的損失的表達式就為：

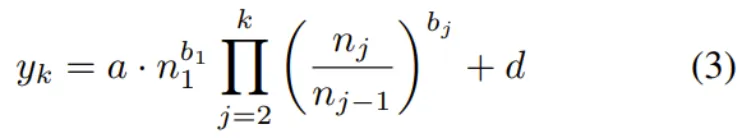
其中 n_j 是在第 j 輪訓練 epoch 結束時的模型看到的樣本數量。這一等式是新提出的擴展律的基礎。

最后，還有一層復雜性，即異構的網絡數據。

然后就得到了他們給出的定理：給定隨機均勻采樣的 p 個數據池，其各自的效用和重復參數分別為 (b_1, τ_1)...(b_p, τ_p)，則每個 bucket 的新重復半衰期就為 τ? = p?τ。此外，組合后的數據池在第 k 輪重復時的有效效用值 b_eff 是各個效用值的加權平均值。其數學形式為：

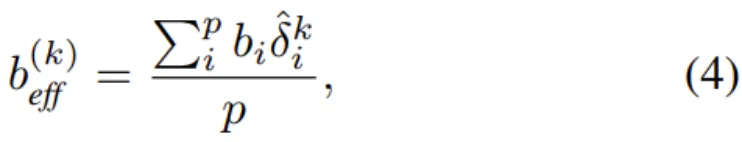
其中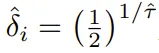，這是新的每 bucket 衰減參數。

最后，可以在 (3) 式中使用上述定理中的 b_eff，就能估計出在數據池組合上進行訓練時的損失。

針對各種數據效用池擬合擴展曲線

該團隊用實驗探究了新提出的擴展律。

圖 4 給出了擬合后的各種數據效用池的擴展曲線，其使用的數據效用指標是 T-MARS 分數。

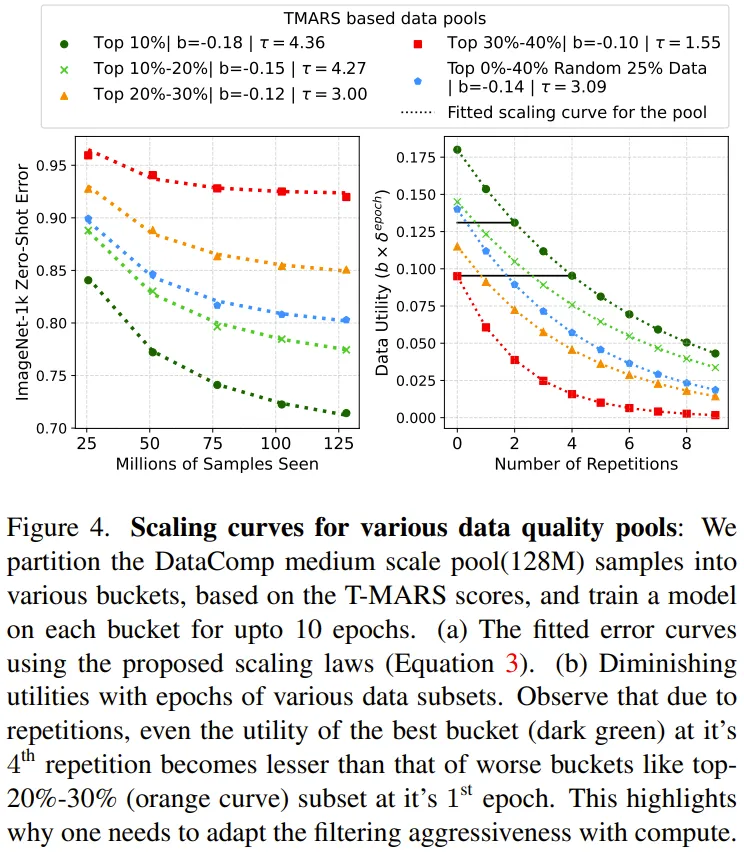
圖 4 的第 2 列表明各個數據池的效用會隨 epoch 增多而降低。下面是該團隊給出的一些重要觀察結果：

1. 網絡數據是異構的，無法通過單一一組擴展參數進行建模。

2. 不同數據池有不同的數據多樣性。

3. 具有重復現象的高質量數據的效果趕不上直接使用低質量數據。

結果：在 QQT 下為數據組合估計擴展律

前面針對不同質量的數據池推斷了各自相應的參數 a、b、d、τ。而這里的目標是確定當給定了訓練計算預算時，最有效的數據整編策略是什么。

通過前面的定理以及各個數據池的擴展參數，現在就能估計不同池組合的擴展律了。舉個例子，可以認為 Top-20% 池是 Top-10% 和 Top 10%-20% 池的組合。然后，這種來自擴展曲線的趨勢就可以用于預測給定計算預算下的帕累托最優數據過濾策略。

圖 5 給出了不同數據組合的擴展曲線，這是在 ImageNet 上評估的。

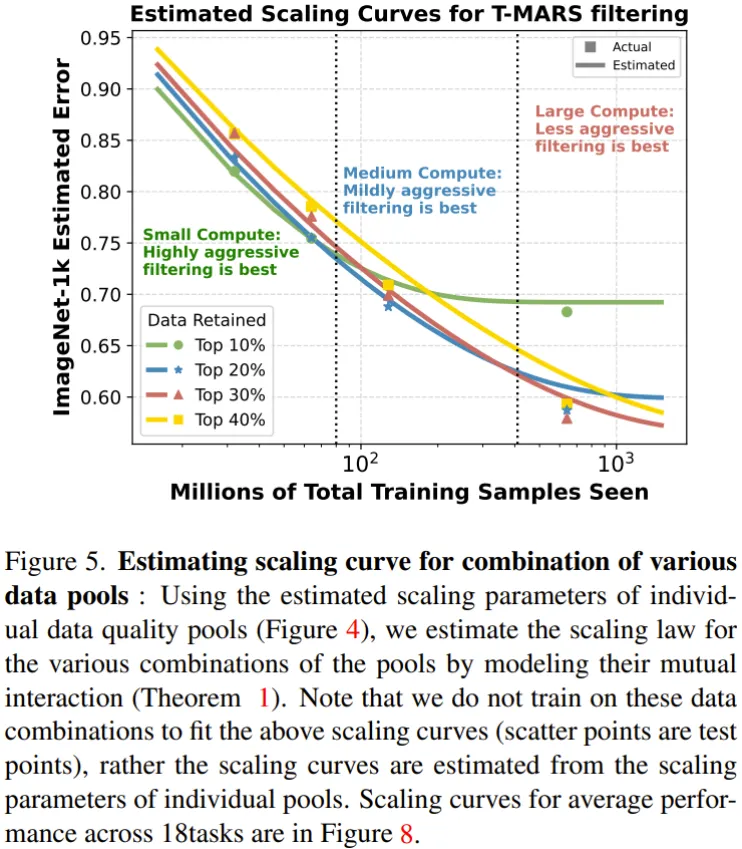
這里需要強調，這些曲線是基于上述定理，直接根據各個組成池的擴展參數估計的。他們并未在這些數據池組合上訓練來估計這些擴展曲線。散點是實際的測試性能，其作用是驗證估計得到的結果。

可以看到：（1）當計算預算低 / 重復次數少時，激進的過濾策略是最好的。

（2）數據整編不能脫離計算進行。

對擴展曲線進行擴展

2023 年 Cherti et al. 的論文《Reproducible scaling laws for contrastive language-image learning》研究了針對 CLIP 模型提出的擴展律，其中訓練了計算規模在 3B 到 34B 訓練樣本之間的數十個模型，并且模型涵蓋不同的 ViT 系列模型。在這樣的計算規模上訓練模型的成本非常高。Cherti et al. (2023) 的目標是為這一系列的模型擬合擴展律，但對于在小數據集上訓練的模型，其擴展曲線有很多錯誤。

CMU 這個團隊認為這主要是因為他們沒考慮到重復使用數據造成的效用下降問題。于是他們使用新提出的擴展律估計了這些模型的誤差。

圖 6 是修正之后擴展曲線，其能以很高的準確度預測誤差。

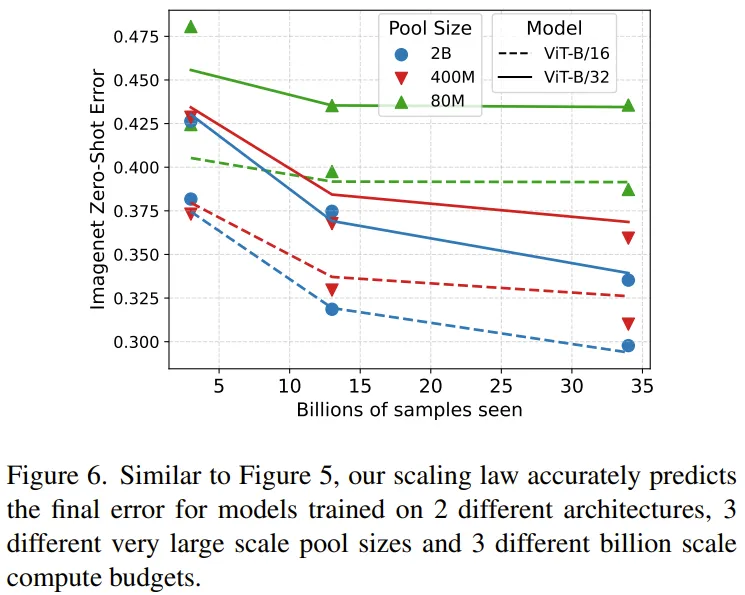
這表明新提出的擴展律適用于用 34B 數據計算訓練的大型模型，這說明在預測模型訓練結果時，新的擴展律確實能考慮到重復數據的效用下降情況。

更多技術細節和實驗結果請參閱原論文。