時間序列預測:探索性數據分析和特征工程的實用指南
時間序列分析是數據科學和機器學習領域最廣泛的主題之一:無論是預測金融事件、能源消耗、產品銷售還是股票市場趨勢,這一領域一直是企業非常感興趣的領域。
隨著機器學習模型的不斷進步,使除了傳統的統計預測方法(如回歸模型、ARIMA模型、指數平滑)外,與機器學習(如基于樹的模型)和深度學習(如LSTM網絡、cnn、基于Transformer的模型)相關的技術已經出現了一段時間。
盡管這些技術之間存在巨大差異,但無論模型是什么,都必須完成一個初步步驟:探索性數據分析。
在統計學中,探索性數據分析(Exploratory Data Analysis, EDA)是對數據進行分析和可視化,以總結數據的主要特征并從中獲得相關信息的一門學科。這在數據科學領域非常重要,因為它可以為另一個重要步驟奠定基礎:特征工程。
所以我們今天這篇文章將總結一個時間序列數據的分析模板,可以總結和突出數據集的最重要特征。我們將使用一些常見的Python庫,如Pandas、Seaborn和Statsmodel。
為了方便演示,將使用Kaggle的小時能耗數據。該數據集與PJM小時能源消耗數據有關,PJM是美國的一個區域輸電組織,為幾個州提供電力。每小時的電力消耗數據來自PJM的網站,單位是兆瓦。
我在本文中我們將EDA總結為六個步驟:描述性統計、時間圖、季節圖、箱形圖、時間序列分解、滯后分析。
描述性統計
描述性統計是一種匯總統計,用于定量地描述或總結結構化數據集合中的特征。
一些通常用于描述數據集的度量是:集中趨勢度量(例如平均值,中位數),分散度量(例如范圍,標準差)和位置度量(例如百分位數,四分位數)。所有這些都可以用所謂的五數總結來概括,即分布的最小值、第一四分位數(Q1)、中位數或第二四分位數(Q2)、第三四分位數(Q3)和最大值。
在Python中,這些信息可以使用Pandas中眾所周知的describe方法輕松檢索:
import pandas as pd
# Loading and preprocessing steps
df = pd.read_csv('../input/hourly-energy-consumption/PJME_hourly.csv')
df = df.set_index('Datetime')
df.index = pd.to_datetime(df.index)
df.describe()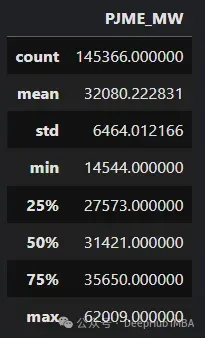
時間曲線圖
最明顯且直觀的圖表是時間圖。觀測結果是根據觀測時間繪制的,連續的觀測結果用線條連接起來。
在Python中,我們可以使用Pandas和Matplotlib:
import matplotlib.pyplot as plt
# Set pyplot style
plt.style.use("seaborn")
# Plot
df['PJME_MW'].plot(title='PJME - Time Plot', figsize=(10,6))
plt.ylabel('Consumption [MW]')
plt.xlabel('Date')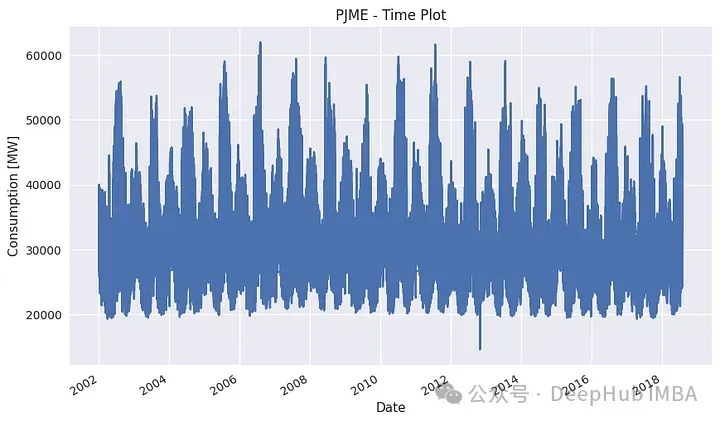
這張圖可以為我們提供一下的信息:
- 模式顯示出每年的季節性。
- 如果只關注一年,似乎會發現更多的規律。由于用電量較大,冬季和夏季的用電量可能會出現高峰。
- 這個數據多年來沒有明顯的增加/減少趨勢,平均消費量保持平穩。
- 2013年前后有一個異常值,可以進行特殊的分析
季節性
季節性圖基本上是一個時間圖,其中數據是根據它們所屬的系列的各個“季節”繪制的。
關于能源消耗,我們通常有每小時可用的數據,因此可以有幾個季節性:每年,每周,每天。在深入研究這些圖之前,讓我們首先在Pandas中設置一些變量:
# Defining required fields
df['year'] = [x for x in df.index.year]
df['month'] = [x for x in df.index.month]
df = df.reset_index()
df['week'] = df['Datetime'].apply(lambda x:x.week)
df = df.set_index('Datetime')
df['hour'] = [x for x in df.index.hour]
df['day'] = [x for x in df.index.day_of_week]
df['day_str'] = [x.strftime('%a') for x in df.index]
df['year_month'] = [str(x.year) + '_' + str(x.month) for x in df.index]1、年消耗量
一個非常有趣的圖是按年按月分組的能源消耗,這突出了年度季節性,可以告訴我們多年來的上升/下降趨勢。
import numpy as np
# Defining colors palette
np.random.seed(42)
df_plot = df[['month', 'year', 'PJME_MW']].dropna().groupby(['month', 'year']).mean()[['PJME_MW']].reset_index()
years = df_plot['year'].unique()
colors = np.random.choice(list(mpl.colors.XKCD_COLORS.keys()), len(years), replace=False)
# Plot
plt.figure(figsize=(16,12))
for i, y in enumerate(years):
if i > 0:
plt.plot('month', 'PJME_MW', data=df_plot[df_plot['year'] == y], color=colors[i], label=y)
if y == 2018:
plt.text(df_plot.loc[df_plot.year==y, :].shape[0]+0.3, df_plot.loc[df_plot.year==y, 'PJME_MW'][-1:].values[0], y, fnotallow=12, color=colors[i])
else:
plt.text(df_plot.loc[df_plot.year==y, :].shape[0]+0.1, df_plot.loc[df_plot.year==y, 'PJME_MW'][-1:].values[0], y, fnotallow=12, color=colors[i])
# Setting labels
plt.gca().set(ylabel= 'PJME_MW', xlabel = 'Month')
plt.yticks(fnotallow=12, alpha=.7)
plt.title("Seasonal Plot - Monthly Consumption", fnotallow=20)
plt.ylabel('Consumption [MW]')
plt.xlabel('Month')
plt.show()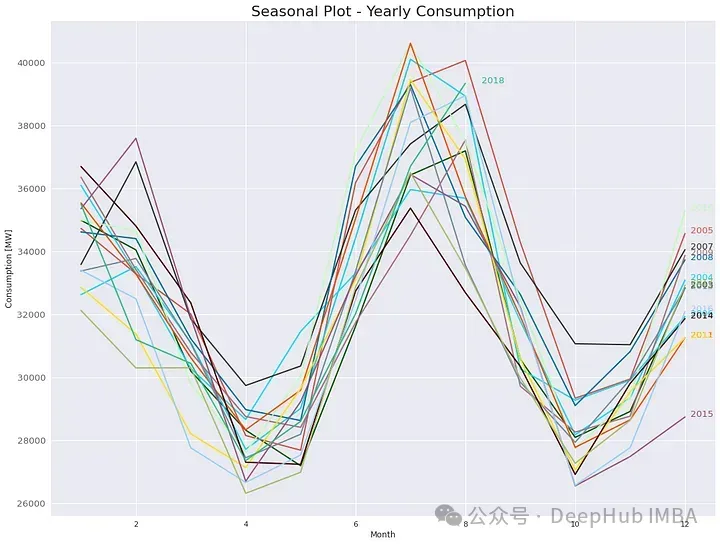
這張圖顯示,每年都有一個預定義的模式:冬季消耗顯著增加,夏季達到峰值(由于供暖/制冷系統),而春季和秋季通常不需要供暖或制冷時消耗最小。這張圖還告訴我們,在多年的總消費量中,并沒有明顯的增加/減少模式。
2、周消耗量
另一個有用的圖表是每周圖表,它描述了幾個月來每周的消費情況,還可以表明每周在一年內是否以及如何變化。
# Defining colors palette
np.random.seed(42)
df_plot = df[['month', 'day_str', 'PJME_MW', 'day']].dropna().groupby(['day_str', 'month', 'day']).mean()[['PJME_MW']].reset_index()
df_plot = df_plot.sort_values(by='day', ascending=True)
months = df_plot['month'].unique()
colors = np.random.choice(list(mpl.colors.XKCD_COLORS.keys()), len(months), replace=False)
# Plot
plt.figure(figsize=(16,12))
for i, y in enumerate(months):
if i > 0:
plt.plot('day_str', 'PJME_MW', data=df_plot[df_plot['month'] == y], color=colors[i], label=y)
if y == 2018:
plt.text(df_plot.loc[df_plot.mnotallow==y, :].shape[0]-.9, df_plot.loc[df_plot.mnotallow==y, 'PJME_MW'][-1:].values[0], y, fnotallow=12, color=colors[i])
else:
plt.text(df_plot.loc[df_plot.mnotallow==y, :].shape[0]-.9, df_plot.loc[df_plot.mnotallow==y, 'PJME_MW'][-1:].values[0], y, fnotallow=12, color=colors[i])
# Setting Labels
plt.gca().set(ylabel= 'PJME_MW', xlabel = 'Month')
plt.yticks(fnotallow=12, alpha=.7)
plt.title("Seasonal Plot - Weekly Consumption", fnotallow=20)
plt.ylabel('Consumption [MW]')
plt.xlabel('Month')
plt.show()
3、每日消費量
最后,我們看看每日消費量。它代表了一天中消費的變化。數據首先按星期進行分組,然后按平均值進行匯總。
import seaborn as sns
# Defining the dataframe
df_plot = df[['hour', 'day_str', 'PJME_MW']].dropna().groupby(['hour', 'day_str']).mean()[['PJME_MW']].reset_index()
# Plot using Seaborn
plt.figure(figsize=(10,8))
sns.lineplot(data = df_plot, x='hour', y='PJME_MW', hue='day_str', legend=True)
plt.locator_params(axis='x', nbins=24)
plt.title("Seasonal Plot - Daily Consumption", fnotallow=20)
plt.ylabel('Consumption [MW]')
plt.xlabel('Hour')
plt.legend()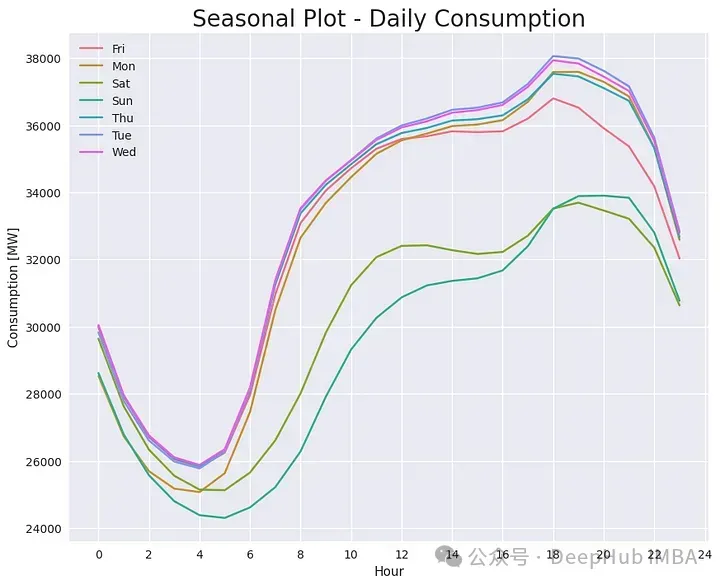
這張圖顯示了一個非常典型的模式,有人稱之為“M輪廓”,因為日消耗似乎描繪了一個“M”。有時這種模式是清晰的
這些圖通常在一天的中間(從上午10點到下午2點)顯示一個相對峰值,然后是一個相對最小值(從下午2點到下午6點)和另一個峰值(從下午6點到晚上8點)。它還顯示了周末和其他日期的消費差異。
4、特征工程
我們如何將這些信息用于特征工程呢?假設我們正在使用一些需要高質量特征的ML模型(例如ARIMA模型或基于樹的模型)。
- 年消費量多年來變化不大這表明如果可能的話,可以使用來自滯后或外生變量的年季節性特征。
- 每周消費在幾個月內遵循相同的模式,可以使用來自滯后或外生變量的每周特征。
- 每天的消費可以使用工作日和周末的分類特征來進行編碼
箱線圖
箱線圖是識別數據分布的有效方法。箱線圖描繪了百分位數,它代表了分布的第一個(Q1)、第二個(Q2/中位數)和第三個(Q3)四分位數,而箱須則代表了數據的范圍。超過須的每一個值都可以被認為是一個離群值,更深入地說,須通常被計算為:
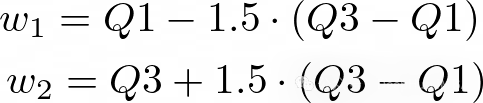
讓我們首先計算總消耗的箱線圖,這可以很容易地在Seaborn中完成:
plt.figure(figsize=(8,5))
sns.boxplot(data=df, x='PJME_MW')
plt.xlabel('Consumption [MW]')
plt.title(f'Boxplot - Consumption Distribution');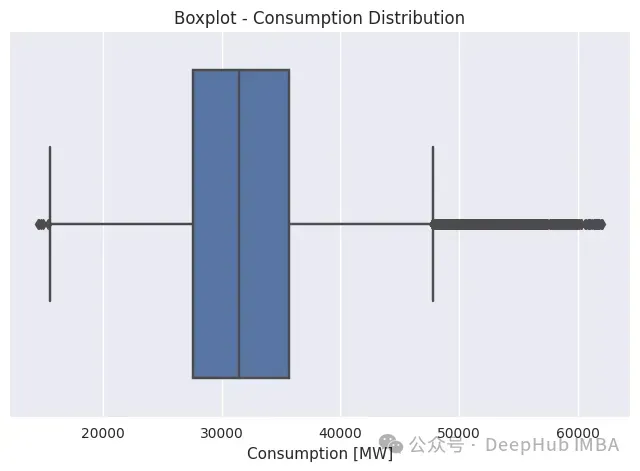
這個圖看起來沒有多少信息,但是它能告訴我們數據是一個類似高斯分布的分布,尾巴更向右突出。
下面是日/月箱形圖。它是通過創建一個“日/月”變量并根據它對消費進行分組而獲得的。以下是2017年以后的代碼
df['year'] = [x for x in df.index.year]
df['month'] = [x for x in df.index.month]
df['year_month'] = [str(x.year) + '_' + str(x.month) for x in df.index]
df_plot = df[df['year'] >= 2017].reset_index().sort_values(by='Datetime').set_index('Datetime')
plt.title(f'Boxplot Year Month Distribution');
plt.xticks(rotatinotallow=90)
plt.xlabel('Year Month')
plt.ylabel('MW')
sns.boxplot(x='year_month', y='PJME_MW', data=df_plot)
plt.ylabel('Consumption [MW]')
plt.xlabel('Year Month')
可以看到,在夏季/冬季(即當我們有高峰時)的不確定性較小,而在春季/秋季(即當溫度變化較大時)則更加分散。2018年夏季的消費量高于2017年,這可能是由于夏季更溫暖。當進行特征工程時,記得包括(如果可用的話)溫度曲線,可能它可以用作外生變量。
另一個有用的圖是一周內的分布,這類似于每周消費季節性圖。
df_plot = df[['day_str', 'day', 'PJME_MW']].sort_values(by='day')
plt.title(f'Boxplot Day Distribution')
plt.xlabel('Day of week')
plt.ylabel('MW')
sns.boxplot(x='day_str', y='PJME_MW', data=df_plot)
plt.ylabel('Consumption [MW]')
plt.xlabel('Day of week')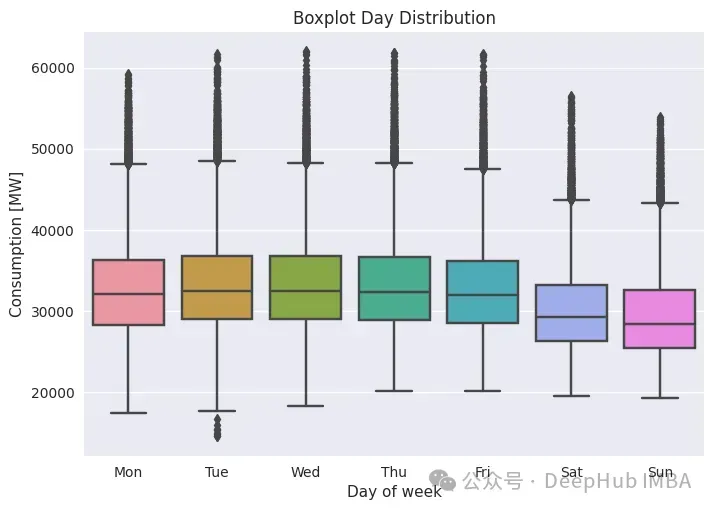
如前所述,周末的消費明顯較低。有幾個異常值能夠看到,像“星期幾”這樣的日歷特征肯定是有用的,但又不能完全解釋。
最后我們來看小時圖。它類似于日消費季節性圖,因為它提供了一天中消費的分布情況。代碼如下:
plt.title(f'Boxplot Hour Distribution');
plt.xlabel('Hour')
plt.ylabel('MW')
sns.boxplot(x='hour', y='PJME_MW', data=df)
plt.ylabel('Consumption [MW]')
plt.xlabel('Hour')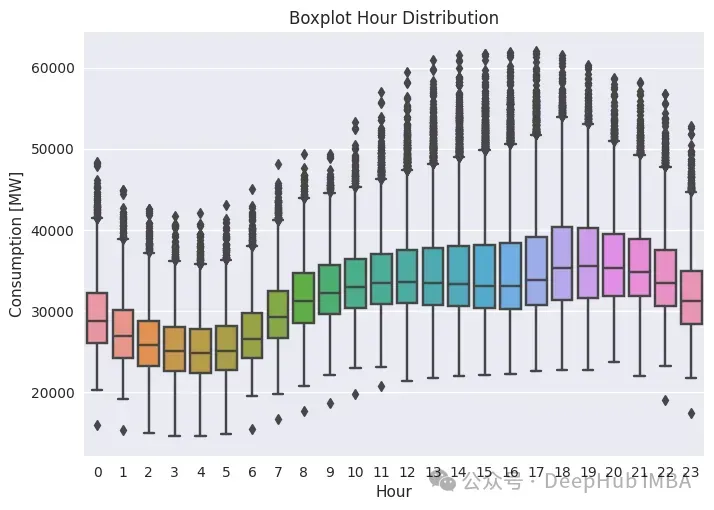
之前看到的“M”形現在更碎了。此外,還有很多異常值,這告訴我們數據不僅依賴于日常季節性(例如,今天12點的消費量與昨天12點的消費量相似),還依賴于其他一些東西,可能是一些外生氣候特征,如溫度或濕度。
時間序列分解
時間序列數據可以顯示各種模式。將時間序列分成幾個組件是有幫助的,每個組件表示一個潛在的模式類別。
我們可以認為一個時間序列由三個部分組成:趨勢部分,季節部分和剩余(偏差)部分(包含時間序列中的任何其他部分)。對于某些時間序列(例如,能源消耗序列),可以有多個季節分量,對應于不同的季節周期(日、周、月、年)。
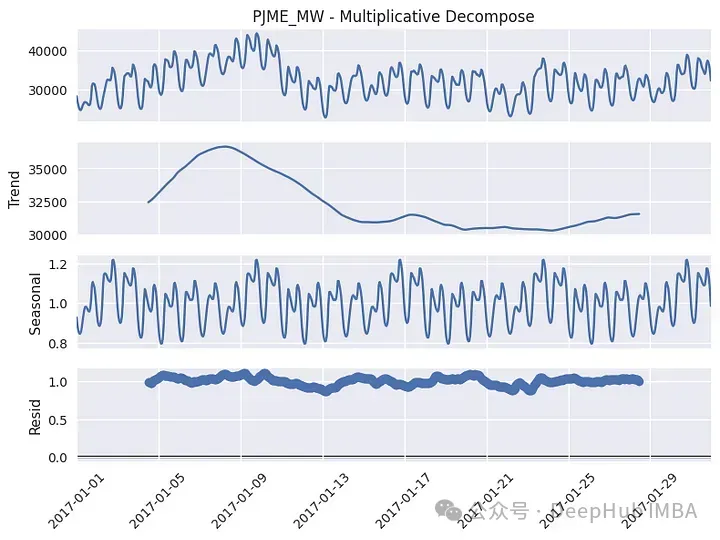
分解有兩種主要類型:加性分解和乘法分解。
對于加性分解,我們將一個序列(整數)表示為季節分量(??)、趨勢分量(??)和余數(??)的和:
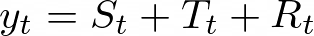
類似地,乘法分解可以寫成:

一般來說,加性分解最適合方差恒定的序列,而乘法分解最適合方差非平穩的時間序列。
在Python中,時間序列分解可以通過Statsmodel庫輕松實現:
df_plot = df[df['year'] == 2017].reset_index()
df_plot = df_plot.drop_duplicates(subset=['Datetime']).sort_values(by='Datetime')
df_plot = df_plot.set_index('Datetime')
df_plot['PJME_MW - Multiplicative Decompose'] = df_plot['PJME_MW']
df_plot['PJME_MW - Additive Decompose'] = df_plot['PJME_MW']
# Additive Decomposition
result_add = seasonal_decompose(df_plot['PJME_MW - Additive Decompose'], model='additive', period=24*7)
# Multiplicative Decomposition
result_mul = seasonal_decompose(df_plot['PJME_MW - Multiplicative Decompose'], model='multiplicative', period=24*7)
# Plot
result_add.plot().suptitle('', fnotallow=22)
plt.xticks(rotatinotallow=45)
result_mul.plot().suptitle('', fnotallow=22)
plt.xticks(rotatinotallow=45)
plt.show()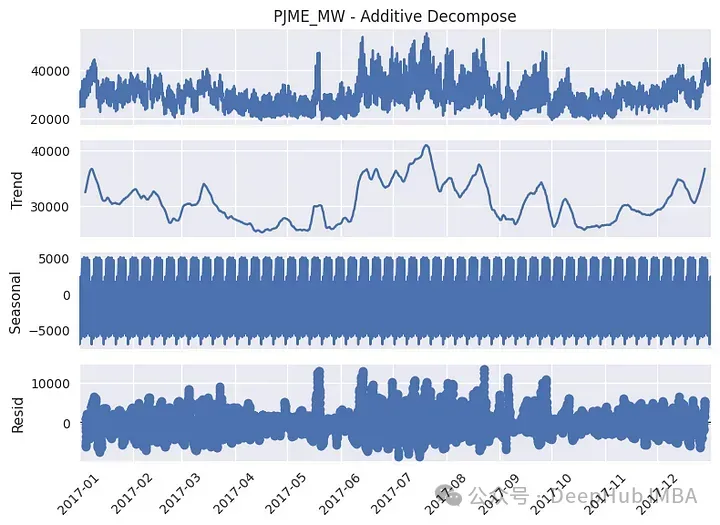
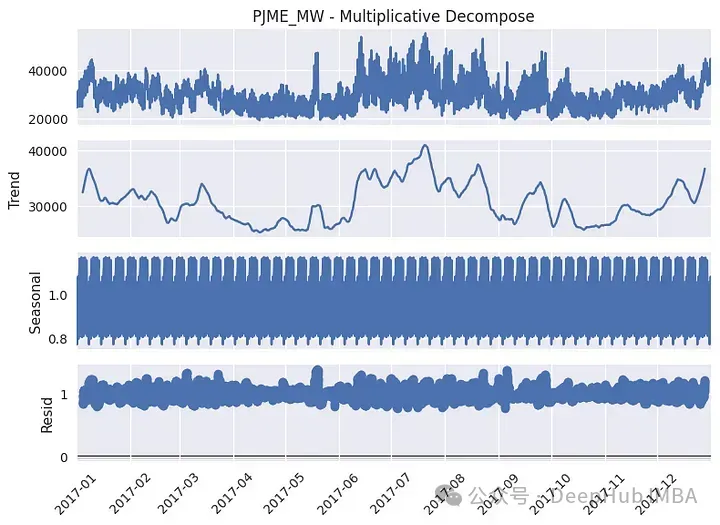
以上圖為2017年的數據。我們看到趨勢有幾個局部峰值,夏季的值更高。從季節成分來看,可以看到實際上有幾個周期性,該圖更突出了周周期性,但如果我們關注同年的一個特定月份(1月),也會出現日季節性:
df_plot = df[(df['year'] == 2017)].reset_index()
df_plot = df_plot[df_plot['month'] == 1]
df_plot['PJME_MW - Multiplicative Decompose'] = df_plot['PJME_MW']
df_plot['PJME_MW - Additive Decompose'] = df_plot['PJME_MW']
df_plot = df_plot.drop_duplicates(subset=['Datetime']).sort_values(by='Datetime')
df_plot = df_plot.set_index('Datetime')
# Additive Decomposition
result_add = seasonal_decompose(df_plot['PJME_MW - Additive Decompose'], model='additive', period=24*7)
# Multiplicative Decomposition
result_mul = seasonal_decompose(df_plot['PJME_MW - Multiplicative Decompose'], model='multiplicative', period=24*7)
# Plot
result_add.plot().suptitle('', fnotallow=22)
plt.xticks(rotatinotallow=45)
result_mul.plot().suptitle('', fnotallow=22)
plt.xticks(rotatinotallow=45)
plt.show()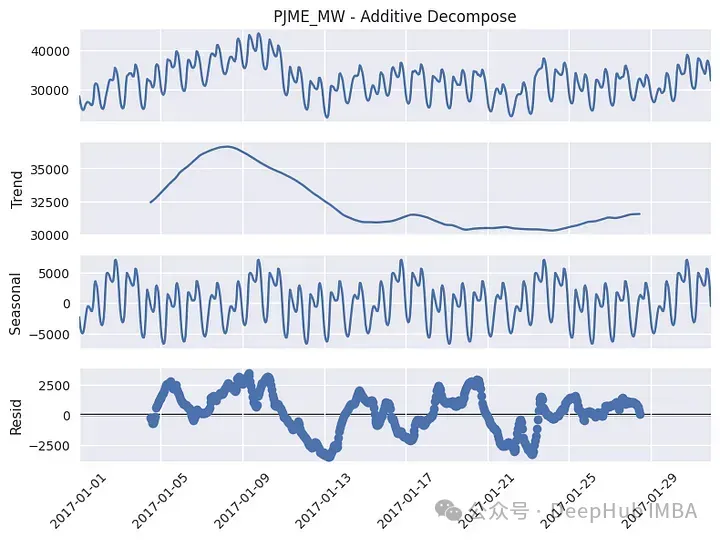
滯后分析
在時間序列預測中,滯后僅僅是序列的過去值。例如,對于每日序列,第一個滯后是指該序列前一天的值,第二個滯后是指再前一天的值,以此類推。
滯后分析是基于計算序列和序列本身的滯后版本之間的相關性,這也稱為自相關。對于一個序列的k滯后版本,我們定義自相關系數為:

其中y 表示序列的平均值,k表示滯后值。
自相關系數構成了序列的自相關函數(ACF),描繪了自相關系數與考慮的滯后數的關系。
當數據具有趨勢時,小滯后的自相關通常很大且為正,因為時間上接近的觀測值在值上也相近。當數據顯示季節性時,季節性滯后(及其季節周期的倍數)的自相關值會比其他滯后的大。具有趨勢和季節性的數據將顯示這些效應的組合。
在實踐中,更有用的函數是偏自相關函數(PACF)。它類似于ACF但是它只顯示兩個滯后之間的直接自相關。例如,滯后3的偏自相關指的是滯后1和2無法解釋的唯一相關性。或者說偏相關指的是某個滯后對當前時間值的直接影響。
如果序列是平穩的,則自相關系數會更清晰地顯現,因此通常最好先對序列進行差分以穩定信號。
下面是繪制一天中不同時段PACF的代碼:
from statsmodels.graphics.tsaplots import plot_pacf
actual = df['PJME_MW']
hours = range(0, 24, 4)
for hour in hours:
plot_pacf(actual[actual.index.hour == hour].diff().dropna(), lags=30, alpha=0.01)
plt.title(f'PACF - h = {hour}')
plt.ylabel('Correlation')
plt.xlabel('Lags')
plt.show()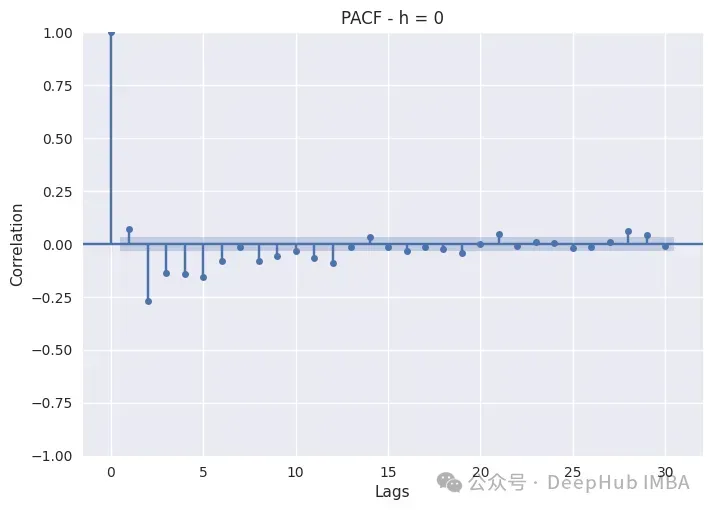
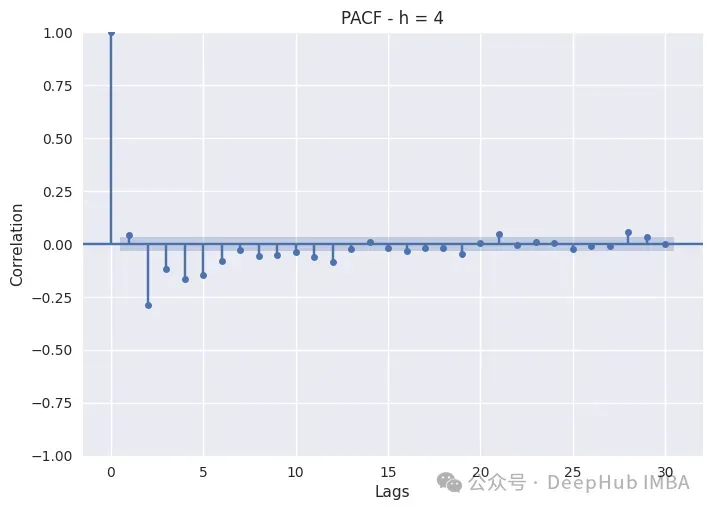
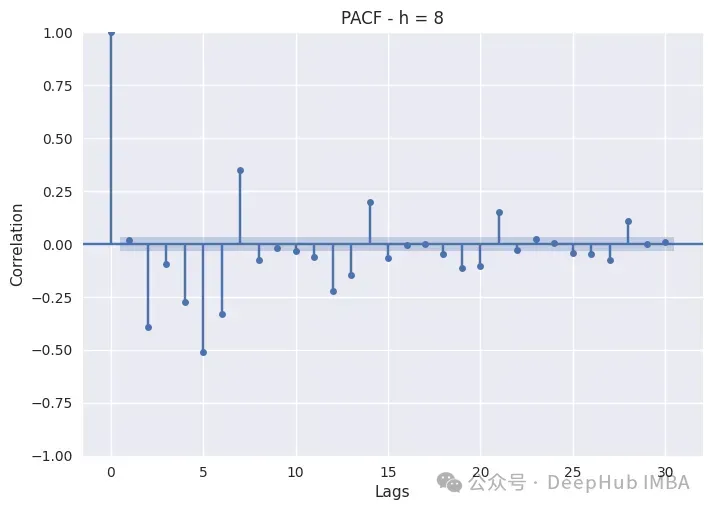
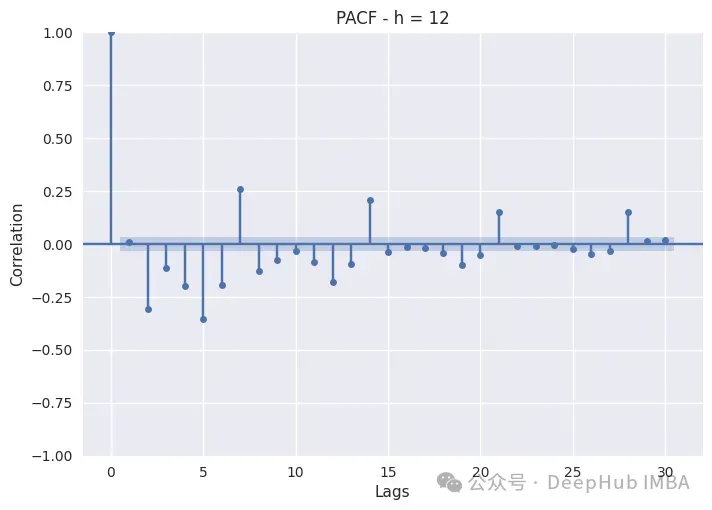
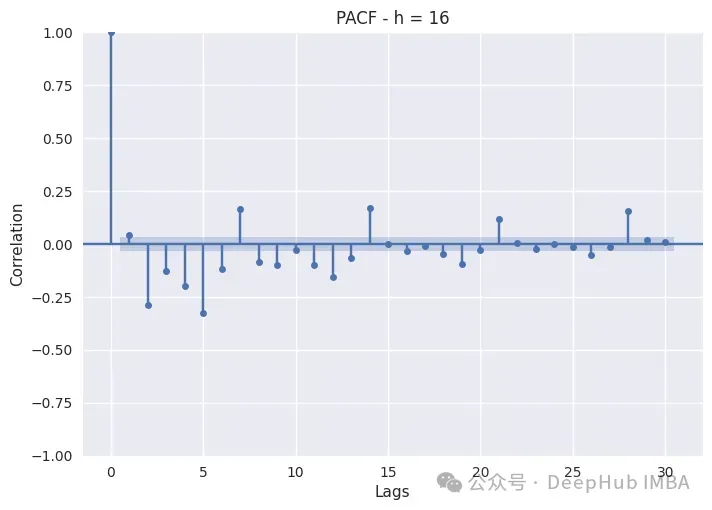
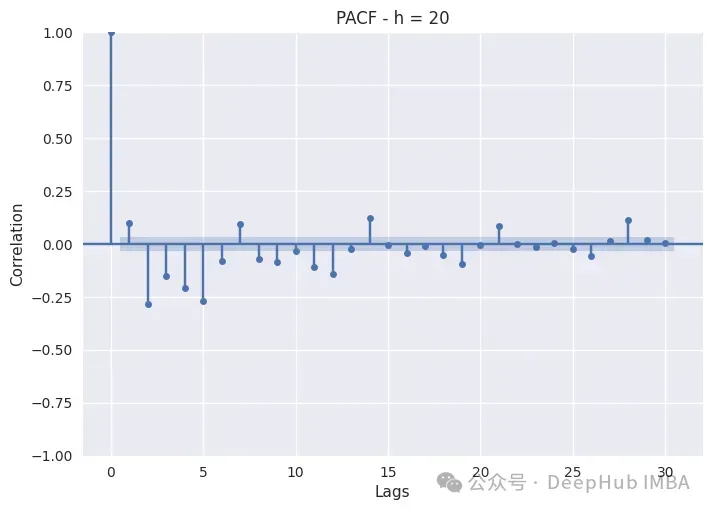
PACF只是繪制不同滯后的Pearson偏自相關系數。非滯后序列顯示出與自身完美的自相關,因此滯后0將始終為1。藍色帶表示置信區間:如果滯后超過該帶,則它具有統計顯著性,我們可以斷言它具有非常重要的意義。
工程特性
滯后分析是時間序列特征工程中最具影響力的研究之一。具有高相關性的滯后是序列中重要的特征,因此應該考慮在內。
一個廣泛使用的特征工程技術是對數據集進行按小時劃分。將數據分成24個子集,每個子集對應一天中的一個小時。這樣做可以規范和平滑信號,使預測變得更簡單。
然后應對每個子集進行特征工程、訓練和微調。最終的預測將通過結合這24個模型的結果來實現。每個小時模型都有其特點,大多數將涉及重要的滯后。
我們簡單介紹在進行滯后分析時可以處理的兩種類型的滯后:
- 自回歸滯后:接近滯后0的滯后,我們預期這些滯后值較高(最近的滯后更有可能預測當前值)。它們是序列顯示趨勢的表現。
- 季節性滯后:指季節周期的滯后。在按小時分割數據時,它們通常代表周度季節性。
自回歸滯后1也可以被認為是序列的日度季節性滯后。
以我們看到的上圖為例:
夜間時間(0,4)的消耗更多地依賴于自回歸,而不是每周滯后,因為最相關的都在前五個小時。像7、14、21、28這樣的季節似乎并不太重要,所以特征工程師時特別注意滯后1到滯后5。
白天時間(8,12,16,20)的消耗表現出自回歸和季節性滯后。這在8小時和12小時尤其如此,因為這兩個小時的消耗量特別高,而隨著夜幕降臨,季節性滯后變得不那么重要了。對于這些子集,我們還應該包括季節性滯后和自回歸。
最后還有一些特征工程滯后的提示:
不要考慮太多的滯后,因為這可能會導致過度擬合。一般自回歸滯后為1 ~ 7,周滯后為7、14、21、28。但并不是必須把它們都當作特征。
考慮非自回歸或季節性的滯后通常是一個壞主意,因為它們也可能導致過擬合。
對滯后進行一些簡單的轉換通常可以產生更強大的特征。例如,季節性滯后可以使用加權平均值進行匯總,以創建代表該系列季節性的單個特征。
總結
本文的目的是為時間序列預測提供一個全面的探索性數據分析模板。
EDA是任何類型的數據科學研究的基本步驟,它允許理解數據的性質和特性,并為特征工程奠定基礎,而特征工程反過來又可以顯著提高模型性能。
我們描述了一些最常用的時間序列EDA分析,這些分析可以是統計/數學和圖形。這項工作的目的只是提供一個實用的框架來開始,后續的調查需要根據所檢查的歷史系列的類型和業務背景進行。