本文經(jīng)計算機視覺研究院公眾號授權(quán)轉(zhuǎn)載，轉(zhuǎn)載請聯(lián)系出處。

論文地址：https://arxiv.org/pdf/2312.10794.pdf

2017 年，Vaswani 等人發(fā)表的 《Attention is all you need》成為神經(jīng)網(wǎng)絡(luò)架構(gòu)發(fā)展的一個重要里程碑。這篇論文的核心貢獻是自注意機制，這是 Transformers 區(qū)別于傳統(tǒng)架構(gòu)的創(chuàng)新之處，在其卓越的實用性能中發(fā)揮了重要作用。

事實上，這一創(chuàng)新已成為計算機視覺和自然語言處理等領(lǐng)域人工智能進步的關(guān)鍵催化劑，同時在大語言模型的出現(xiàn)中也起到了關(guān)鍵作用。因此，了解 Transformers，尤其是自注意處理數(shù)據(jù)的機制，是一個至關(guān)重要但在很大程度上尚未充分研究的領(lǐng)域。

深度神經(jīng)網(wǎng)絡(luò)（DNNs）有一個共同特征：輸入數(shù)據(jù)按照順序，被逐層處理，形成一個時間離散的動態(tài)系統(tǒng)（具體內(nèi)容可以參考 MIT 出版的《深度學(xué)習(xí)》，國內(nèi)也被稱為「花書」）。這種觀點已被成功地用于將殘差網(wǎng)絡(luò)建模到時間連續(xù)的動態(tài)系統(tǒng)上，后者被稱為神經(jīng)常微分方程（neural ODEs）。在神經(jīng)常微分方程中，輸入圖像 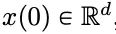在時間間隔 （0，T） 上會按照給定的時變速度場 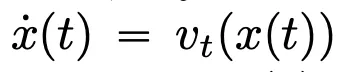進行演化。因此，DNN 可以看作是從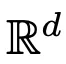一個  到另一個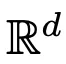的流映射（Flow Map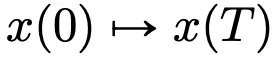）。即使在經(jīng)典 DNN 架構(gòu)限制下的速度場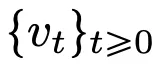中，流映射之間也具有很強的相似性。

研究者們發(fā)現(xiàn)，Transformers 實際上是在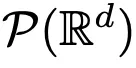上的流映射，即 d 維概率測度空間（the space of probability measures）間的映射。為了實現(xiàn)這種在度量空間間進行轉(zhuǎn)換的流映射，Transformers 需要建立了一個平均場相互作用的粒子系統(tǒng)（mean-field interacting particle system.）。

具體來說，每個粒子（在深度學(xué)習(xí)語境下可以理解為 token）都遵循向量場的流動，流動取決于所有粒子的經(jīng)驗測度（empirical measure）。反過來，方程決定了粒子經(jīng)驗測量的演變進程，這個過程可能會持續(xù)很長時間，需要進行持續(xù)關(guān)注。

對此，研究者的主要觀察結(jié)果是，粒子們往往最終會聚集到一起。這種現(xiàn)象在諸如單向推導(dǎo)（即預(yù)測序列中的下一個詞）的學(xué)習(xí)任務(wù)中會尤為明顯。輸出度量對下一個 token 的概率分布進行編碼，根據(jù)聚類結(jié)果就可以篩選出少量可能的結(jié)果。

本文的研究結(jié)果表明，極限分布實際上是一個點質(zhì)量，不存在多樣性或隨機性，但這與實際觀測結(jié)果不符。這一明顯的悖論因粒子存在長時間的可變狀態(tài)得到解決。從圖 2 和圖 4 中可以看出，Transformers 具有兩種不同的時間尺度：在第一階段，所有 token 迅速形成幾個簇，而在第二階段（較第一階段速度慢得多），通過簇的成對合并過程，所有 token 最終坍縮為一個點。

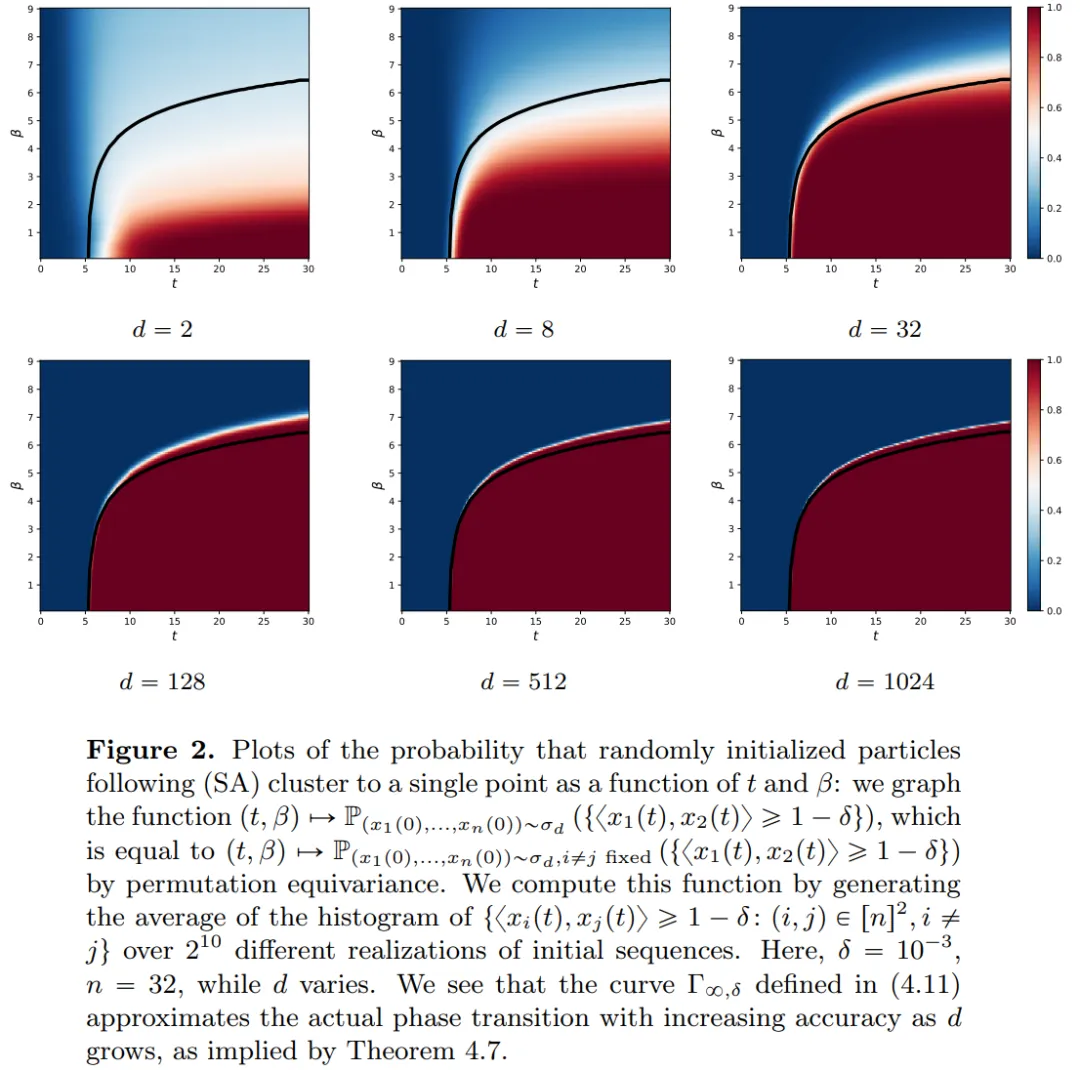
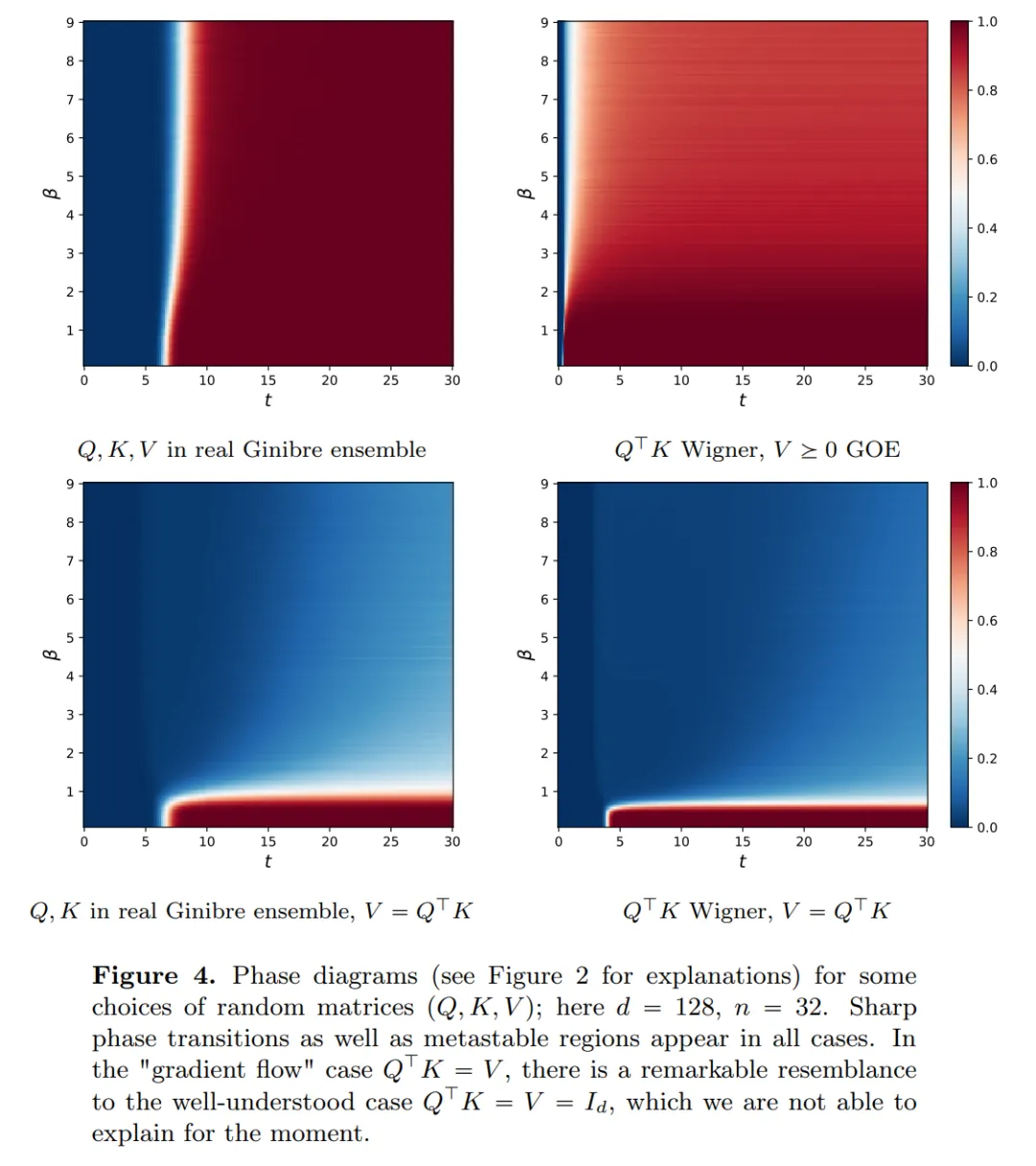
本文的目標有兩個方面。一方面，本文旨在提供一個從數(shù)學(xué)角度研究 Transformers 通用且易于理解的框架。特別是，通過這些相互作用粒子系統(tǒng)的結(jié)構(gòu)，研究者可以將其與數(shù)學(xué)中的既定主題建立具體聯(lián)系，包括非線性傳輸方程、Wasserstein 梯度流、集體行為模型和球面上點的最優(yōu)化配置等。另一方面，本文描述了幾個有前景的研究方向，并特別關(guān)注長時間跨度下的聚類現(xiàn)象。研究者提出的主要結(jié)果指標都是新的，并且還在整篇論文中提出了他們認為有趣的開放性問題。

本文的主要貢獻分為三個部分。

第 1 部分：建模。本文定義了 Transformer 架構(gòu)的理想模型，該模型將層數(shù)視為連續(xù)時間變量。這種抽象方法并不新穎，與 ResNets 等經(jīng)典架構(gòu)所采用的方法類似。本文的模型只關(guān)注 Transformer 架構(gòu)的兩個關(guān)鍵組成部分：自注意力機制和層歸一化。層歸一化有效地將粒子限制在單位球 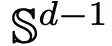的空間內(nèi)部，而自注意力機制則是通過經(jīng)驗度量實現(xiàn)粒子之間的非線性耦合。反過來，經(jīng)驗度量根據(jù)連續(xù)性偏微分方程進行演化。本文還為自注意引入了一個更簡單好用的替代模型，一個能量函數(shù)的 Wasserstein 梯度流，而能量函數(shù)在球面上點的最優(yōu)配置已經(jīng)有成熟的研究方法。

第二部分：聚類。在這一部分，研究者提出了在較長時間跨度下，token 聚類的新的數(shù)學(xué)結(jié)果。如定理 4.1 表明，在高維空間中，一組隨機初始化在單位球上的 n 個粒子會在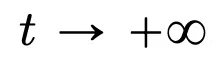時聚成一個點。研究者對粒子集群收縮率的精確描述對這一結(jié)果進行了補充說明。具體來說，研究者繪制了所有粒子間距離的直方圖，以及所有粒子快要完成聚類的時間點（見原文第 4 節(jié)）。研究者還在不假設(shè)維數(shù) d 較大的情況下就得到了聚類結(jié)果（見原文第 5 節(jié)）。

第 3 部分：未來展望。本文主要以開放式問題的形式提出問題，并通過數(shù)字觀測加以證實，以此提出了未來研究的潛在路線。研究者首先關(guān)注維數(shù) d = 2 的情況（見原文第 6 節(jié)），并引出與 Kuramoto 振蕩器的聯(lián)系。然后簡要展示了如何通過對模型進行簡單而自然的修改，解決球面最優(yōu)化相關(guān)的難題（見原文第 7 節(jié)）。接下來的章節(jié)探討了相互作用的粒子系統(tǒng)，這些粒子系統(tǒng)使得對 Transformer 架構(gòu)中的參數(shù)進行調(diào)整成為可能，日后可能會進一步產(chǎn)生實際應(yīng)用。