ICML 2024|Transformer究竟如何推理?基于樣例還是基于規則
本文經計算機視覺研究院公眾號授權轉載,轉載請聯系出處。

- 論文地址:https://arxiv.org/abs/2402.17709
- 項目主頁:https://github.com/GraphPKU/Case_or_Rule
- 論文標題:Case-Based or Rule-Based: How Do Transformers Do the Math?
Case-based or rule-based?
人類可以輕松地學習加法的基本規則,例如豎式加法,并將其應用于任意長度的新的加法問題,但 LLMs 卻難以做到這一點。相反,它們可能會依賴于訓練語料庫中見過的相似樣例來幫助解決問題。來自北京大學張牧涵團隊的 ICML 2024 論文深刻研究了這一現象。研究者們將這兩種不同的推理機制定義為 “基于規則的推理”(rule-based reasoning)和 “基于樣例的推理”(case-based reasoning)。圖 1 展現了兩種推理機制在遇到同一個加法問題時,采用的不同模式。
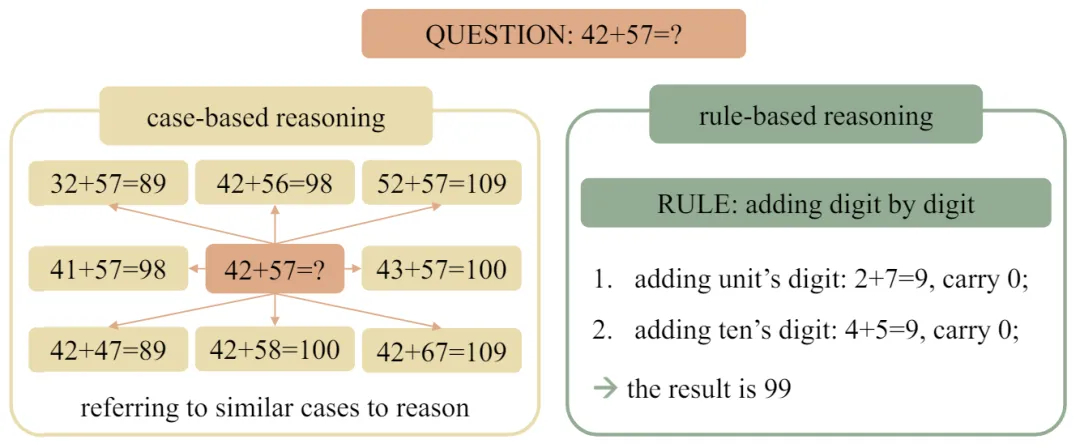
圖 1:case-based reasoning 與 rule-based reasoning 示意圖
由于 rule-based reasoning 對于獲得系統性的泛化能力 (systematic generalization) 至關重要,作者在文章中探討了 transformers 在數學問題(例如 "")中到底是使用何種推理機制。為了測試模型是否依賴特定樣例來解決問題,作者使用了 Leave-Square-Out 方法。主要思想是首先需要定位模型可能依賴的訓練集中的樣例,然后將它們從訓練集中移除,以觀察它們是否影響模型的測試性能。對于數學推理,作者的假設是,在解決某個測試樣本時,transformers 傾向于依賴與測試樣本 “接近” 的訓練樣本來進行推理。因此,作者在樣本的二維空間中挖掉了一塊正方形作為測試集(test square)。根據假設,若模型在做 case-based reasoning,且模型依賴的是與 test sample 距離較近的 training sample 來做推理,那么模型將無法答對正方形中心附近的 test samples,因為模型在訓練集中沒有見過接近的樣例。
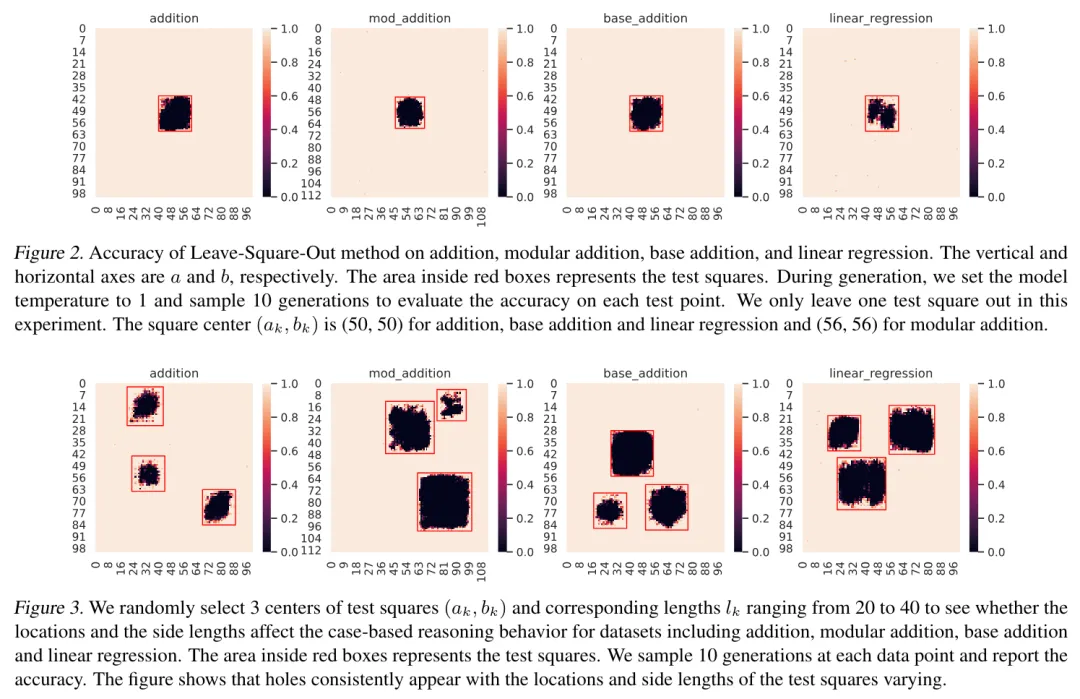
圖 2:GPT-2 在加法、模加法、九進制加法、線性回歸上利用 Leave-Square-Out 方法進行 fine-tune 后在全數據集上的正確率。其中,紅框中的方形區域為測試集,其他部分為訓練集合。
通過在五個數學任務(包括加法、模加法、九進制加法、線性回歸以及雞兔同籠問題)的干預實驗,transformers 無一例外都表現出了 case-based reasoning 的行為。作者利用 Leave-Square-Out 方法對 GPT-2 進行了 fine-tune,具體的模型表現展示于圖 2。可見,測試集內,模型的性能由邊界到中心迅速下降,出現了 holes。這說明當我們把 holes 周圍的 similar cases 移出訓練集時,模型便無法做對 holes 中的 test samples 做出準確推理。也即展現出模型依賴 similar cases 進行推理的行為。為了確保結論的公平性,作者同時利用 random split 方法對數據集進行了訓練集 / 測試集的劃分,并觀察到 random split 下模型可輕易在測試集上達到接近 100% 的準確率,說明 Leave-Square-Out 實驗中的訓練樣例數是足夠模型完成推理的,且再次側面印證了 transformers 在做基于樣例的推理(因為 random split 下所有 test samples 都有接近的 training samples)。
Scratchpad 是否會改變模型推理行為?
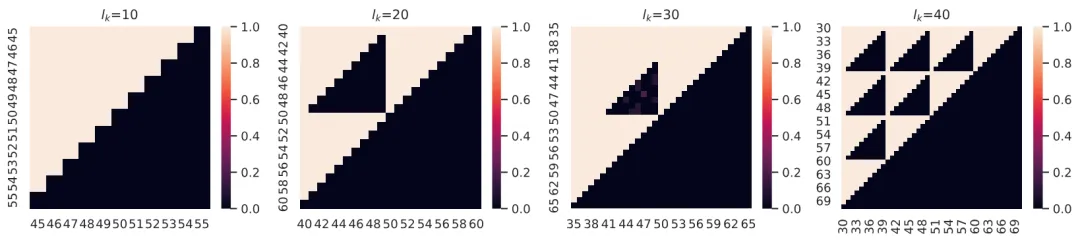
圖 3:利用 scratchpad 對 GPT-2 在加法任務上進行 fine-tune 后的模型在 test square 中的準確率。
此外,作者探討了是否可以通過加入 scratchpad,即引導模型在輸出中一位一位地做加法來消除 case-based reasoning 的行為,使模型轉向 rule-based reasoning(scratchpad 的具體方法可見圖 4)。圖 3 展示了利用 scratchpad 對 GPT-2 在加法任務上進行 fine-tune 后的模型在 test square 中的準確率。
一方面,可發現 test square 中仍然有一部分模型無法做對的區域,表現出模型仍然在做 case-based reasoning;另一方面,與不加入 scratchpad 時模型在 test square 中出現整塊連續的 hole 的現象相比,模型在使用 scratchpad 時對于訓練樣例的依賴情況顯然發生了變化。
具體而言,test square 中無法做對的區域呈現為三角形,其斜邊沿著個位和十位的 “進位邊界”。例如,圖 3 中自左向右第 2 張圖(test square 邊長)有兩個三角形區域,模型的準確率幾乎為零。小三角形表示,模型無法解決如47+48的問題,因為訓練集中沒有包含十位上進位的步驟(所有四十幾 + 四十幾的樣例都在測試集中)。而對于不涉及十位進位的測試樣本,如42+43 ,模型則能夠成功,因為它可以從大量其他訓練數據中學習到 4+4這個中間步驟(例如)。對于大三角形中的數據而言,模型無法解決例如57+58這樣的問題,因為訓練集中沒有包含十位上需要進位到百位的案例。
這些黑色區域的形狀和位置表明,只有當測試案例的每一步在訓練集中都出現過時,模型才能夠成功;否則就會失敗。更重要的是,這一現象表明,即使有 step-by-step 的推理過程的幫助,transformers 也難以學會 rule-based reasoning —— 模型仍然在機械地記憶見過的單個步驟,而沒有學會背后的規則。
其他影響因素
Scratchpad 以外,作者也在文章中對 test square 的位置、大小,模型的大小(包括 GPT-2-Medium,與更大的模型:Llama-2-7B 和 GPT-3.5-Turbo),數據集的大小等因素進行了豐富的測試。模型在做 case-based reasoning 的結論是統一的。具體的實驗細節可見文章。
Rule-Following Fine-Tuning (RFFT)
通過上述的干預實驗,作者發現 transformers 在數學推理中傾向于使用 case-based reasoning,然而,case-based reasoning 會極大地限制模型的泛化能力,因為這意味著模型如果要做對新的 test sample ,就需要在訓練集中見過相似的樣本。而在訓練集中覆蓋到所有未知推理問題的相似樣本是幾乎不可能的(尤其對于存在長度泛化的問題)。
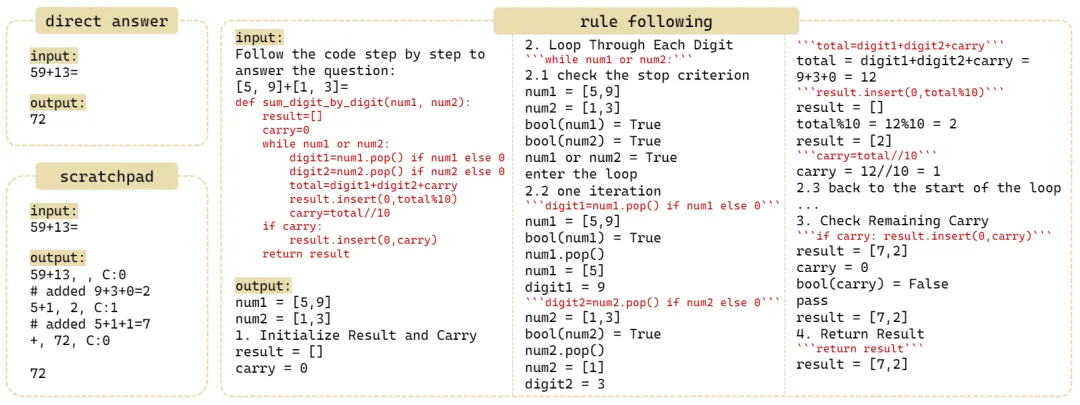
圖 4:direct answer,scratchpad 與 rule-following 三種方法的 input-output sequence
為了緩解此類問題,作者提出了名為 Rule-Following Fine-Tuning(RFFT)的規則遵循微調技術,旨在教 transformers 進行 rule-based reasoning。具體來說,如圖 4 所示,RFFT 在輸入中提供顯式的規則,然后指導 transformers 逐行地回憶規則并執行。
實驗中,作者在 1-5 位數的加法上使用圖 4 所示的三種方法對 Llama-2-7B 和 GPT-3.5-turbo 進行了 fine-tune,并分別在 6-9 與 6-15 位數的 OOD 的加法任務上進行了測試。
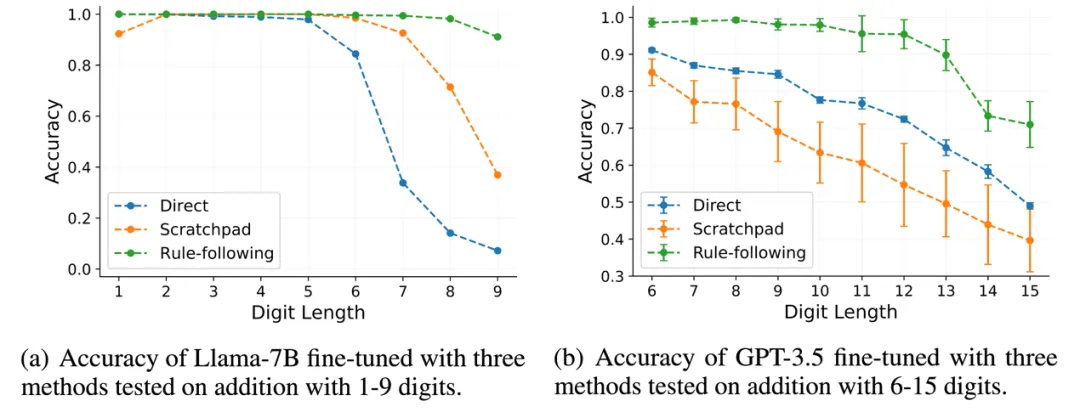
圖 5:Llama-2-7b 和 GPT-3.5-turbo
由圖 5 可見,RFFT 在長度泛化的性能上明顯超過了 direct answer 和 scratchpad 這兩種微調方法。使用 Llama-2-7B 進行 RFFT 時,模型在 9 位數的加法中也能保持 91.1% 的準確率。相比之下,使用 scratchpad 進行 fine-tune 的模型在此任務中的準確率不到 40%。對于擁有更強的基礎能力的 GPT-3.5-turbo,RFFT 使其能夠驚人地泛化到涉及多達 12 位數字的加法,盡管只在 1-5 位加法上訓練了 100 個訓練樣本,但其在 12 位數的加法上仍然保持了 95% 以上的準確率。這也顯著超過了 scratchpad 和 direct answer 的結果。這些結果突出顯示了 RFFT 在引導 transformers 進行 rule-based reasoning 方面的有效性,并展現了其在增強模型長度泛化能力方面的潛力。
值得注意的是,作者發現 Llama-2-7B 需要 150,000 個訓練樣本才能泛化到 9 位數字,而 GPT-3.5 僅用 100 個訓練樣本就能掌握規則并泛化到 12 位數字。因此,規則遵循(rule-following)可能是一種 meta learning ability—— 它可能通過在多樣化的 rule-following 數據上進行訓練而得到加強,并可更容易地遷移到新的未在訓練集中見過的領域中。相應地,基礎模型越強大,理解并學習新的規則就越容易。這也與人類學習新規則的能力相符 —— 經驗豐富的學習者通常學習得更快。
總結
本文探究了 transformers 在做數學推理問題時究竟是采用 case-based reasoning 還是 rule-based reasoning,并提出了 Rule-Following Fine-Tuning 的規則遵循微調方法來顯式地教會 transformers 進行 rule-based reasoning。RFFT 展現了強大的長度泛化能力,并有潛力全面提升 LLMs 的推理能力。