協方差矩陣適應進化算法實現高效特征選擇
在建立模型時，特征選擇是一個重要環節，它指通過保留一部分特征子集來擬合模型，而舍棄其余特征。進行特征選擇有多重原因:
- 保持模型的可解釋性(過多特征會增加解釋難度)
- 避免維數災難
- 優化與模型相關的目標函數(如R平方、AIC等)
- 防止過擬合等
如果特征數量N較小，可使用窮舉搜索嘗試所有可能的特征組合，保留使成本/目標函數最小的那個。但當N較大時，窮舉搜索就行不通了，因為需嘗試的組合數為2^N，這是指數級增長，N超過幾十個就變得極其耗時。
此時需采用啟發式算法，以有效方式探索搜索空間，尋找能使目標函數最小化的特征組合。具體來說，需尋找一個長度為N的0/1向量[1,0,0,1,0,1,1,0,...]，其中1表示選擇該特征，0表示舍棄。目標是找到一個能最小化目標函數的這樣一個向量。搜索空間的維度等于特征數量N，每一維只有0/1兩種取值可能。
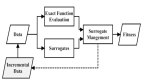
尋找一個好的啟發式算法并非易事。R語言中regsubsets()函數提供了一些選項。Scikit-learn庫也提供了幾種啟發式特征選擇方法，前提是問題能很好地符合它們的技術假設。然而，要找到一種通用的、高效的啟發式算法仍是一個挑戰。在本系列文章中，我們將探討幾種即使在特征數量N很大、目標函數可為任意可計算函數(只要不過于緩慢)的情況下，也能給出合理結果的協方差矩陣適應進化算法方法。
數據集
特征選擇是機器學習中一個重要的預處理步驟,它通過選擇出對預測目標貢獻最大的特征子集,從而提高模型的性能和簡潔性。常見的特征選擇方法包括Filter(過濾式)、Wrapper(包裝式)和Embedded(嵌入式)等。其中,協方差矩陣適應進化算法(Covariance Matrix Adaptation Evolution Strategy, CMA-ES)是一種高效的Wrapper式特征選擇算法。
在本文中，我們將使用著名的房價預測數據集(來自Kaggle[1] ，共213個特征，1453個樣本)對CMA-ES算法的特征選擇能力進行說明。我們所使用的模型是線性回歸模型，目標是最小化貝葉斯信息準則(BIC)，它是一種評估模型質量的指標，值越小表示模型越好。與之類似的指標還有AIC(Akaike信息準則)，兩者都能有效避免過擬合。當然，我們也可以使用R平方或調整R平方作為目標函數，只是需要注意此時目標是最大化而非最小化。
圖片
數據清洗
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import os
import random
import copy
from itertools import repeat
import shutil
import time
import math
import array
df = pd.read_csv('train.csv')
# drop columns with NaN
df.dropna(axis=1, inplace=True)
# drop irrelevant columns
df.drop(columns=['Id'], inplace=True)
# drop major outliers
df = df[df['BsmtFinSF1'] <= 5000]
df = df[df['MiscVal'] <= 5000]
df = df[df['LotArea'] <= 100000]
columns_non_categorical = df.select_dtypes(exclude='object').columns.to_list()
columns_non_categorical.sort()
columns_non_categorical.remove('SalePrice')
columns_non_categorical = ['SalePrice'] + columns_non_categorical
# alphabetically sort columns, keep target first
df_temp = df[['SalePrice']]
df.drop(columns=['SalePrice'], inplace=True)
df.sort_index(axis=1, inplace=True)
df = pd.concat([df_temp, df], axis=1)
del df_temp無論選擇何種評估指標作為目標函數，CMA-ES算法都能通過迭代搜索的方式，找到一個使目標函數值最優的特征子集，從而實現自動高效的特征選擇。下面將對算法的原理和應用進行詳細闡述。
我們將嘗試通過特征選擇來最小化 BIC，因此這里是在啟用所有特征選擇之前，從 statsmodels.api.OLS() 中得到的 BIC 基準值：
X = df.drop(columns=['SalePrice']).copy()
y = df['SalePrice'].copy()
X = add_constant(X)
linear_model = sm.OLS(y, X).fit()
print(f'baseline BIC: {linear_model.bic}')baseline BIC: 34570.166173470934現在，讓我們來看看一種著名的、久經考驗的特征選擇技術，我們將把它與后面介紹的更復雜的技術進行比較。
順序特征搜索(SFS)
順序特征搜索是一種貪婪的特征選擇算法，它包含前向搜索和后向搜索兩種策略。以前向搜索為例，算法流程如下:
- 首先從全部N個特征中選擇一個使目標函數值最優的單特征子集。
- 在已選特征子集的基礎上，再添加一個新特征，形成兩個特征的子集，選擇能使目標函數進一步最小化的那個組合。
- 重復步驟2，每輪迭代都只增加一個新特征，直到所有特征都被嘗試加入子集。
- 從所有被嘗試過的特征子集中，選擇使目標函數值最小的那個作為最終輸出。
SFS是一種貪婪算法，它每一步的選擇都是基于當前最優解的局部決策，無法回頭修正之前的決策。但它的搜索復雜度只有O(N^2)，相比暴力搜索指數級的復雜度，計算效率大幅提高。當然，這種高效是以潛在的全局最優解被忽略為代價的。
SFS的后向策略則是從全量特征集合出發，每輪迭代移除一個使目標函數值改善最小的特征，直至所有特征被遍歷過為止。
使用 mlxtend 庫[2] 編寫的 SFS 代碼在 Python 中是什么樣的：
import statsmodels.api as sm
from mlxtend.feature_selection import SequentialFeatureSelector as SFS
from sklearn.base import BaseEstimator
class DummyEstimator(BaseEstimator):
# mlxtend 希望使用 sklearn 估計器，但這里不需要（使用 statsmodels OLS 代替）。
def fit(self, X, y=None, **kwargs):
return self
def neg_bic(m, X, y):
# objective function
lin_mod_res = sm.OLS(y, X, hascnotallow=True).fit()
return -lin_mod_res.bic
seq_selector = SFS(
DummyEstimator(),
k_features=(1, X.shape[1]),
forward=True,
floating=False,
scoring=neg_bic,
cv=None,
n_jobs=-1,
verbose=0,
# make sure the intercept is not dropped
fixed_features=['const'],
)
n_features = X.shape[1] - 1
objective_runs_sfs = round(n_features * (n_features + 1) / 2)
t_start_seq = time.time()
# mlxtend will mess with your dataframes if you don't .copy()
seq_res = seq_selector.fit(X.copy(), y.copy())
t_end_seq = time.time()
run_time_seq = t_end_seq - t_start_seq
seq_metrics = seq_res.get_metric_dict()它可以快速運行各種組合，這些就是匯總結果：
best k: 36
best objective: 33708.98602877906
R2 @ best k: 0.9075677543649224
objective runs: 22791
total run time: 42.448 sec在 213 個特征中，最佳特征數為 36 個。最佳 BIC 為 33708.986（特征選擇前的基線值為 34570.166），在我的系統上完成這一過程用時不到 1 分鐘。它調用目標函數 22.8k 次。
這些是最佳 BIC 值和 R 方值與所選特征數量的函數關系：
best_objective_seq = -np.inf
r2_of_best_k = 0
r2_list = []
best_k = 1
best_features_seq = []
# also extract R2 from the feature selection search
for k in tqdm(seq_metrics.keys()):
r2_eval_mod = sm.OLS(
y, X[list(seq_metrics[k]['feature_names'])], hascnotallow=True
)
r2_eval_mod_res = r2_eval_mod.fit()
r2 = r2_eval_mod_res.rsquared
r2_list.append(r2)
score_k = seq_metrics[k]['avg_score']
if score_k > best_objective_seq:
best_objective_seq = score_k
best_k = k
best_features_seq = list(seq_metrics[k]['feature_names'])
r2_of_best_k = r2
print(f'best k: {best_k}')
print(f'best objective: {-best_objective_seq}')
print(f'R2 @ best k: {r2_of_best_k}')
print(f'objective runs: {objective_runs_sfs}')
print(f'total run time: {run_time_seq:.3f} sec')
print(f'best features: {best_features_seq}')
sfs_avg = [-seq_metrics[k]['avg_score'] for k in sorted(seq_metrics.keys())]
fig, ax = plt.subplots(1, 2, figsize=(10, 4), layout='constrained')
ax[0].scatter(sorted(seq_metrics.keys()), sfs_avg, s=1)
ax[0].set_xticks(sorted(seq_metrics.keys()), minor=True)
ax[0].set_title('BIC')
ax[0].set_xlabel('number of features')
ax[0].set_ylabel('BIC')
ax[1].scatter(sorted(seq_metrics.keys()), r2_list, s=1)
ax[1].set_title('R2')
ax[1].set_xlabel('number of features')
ax[1].set_ylabel('R2')
fig.suptitle('sequential forward search')
fig.savefig('sfs-performance.png')
fig.show()best k: 36
best objective: 33708.98602877906
R2 @ best k: 0.9075677543649224
objective runs: 22791
total run time: 42.448 sec
best features: ['const', 'BedroomAbvGr', 'BldgType_1Fam', 'BsmtFinSF1', 'Condition1_Norm',
'Condition2_PosN', 'ExterQual_Ex', 'Exterior1st_BrkFace', 'Functional_Sev',
'Functional_Typ', 'GarageArea', 'GrLivArea', 'HeatingQC_Ex', 'KitchenQual_Ex',
'LandContour_HLS', 'LotArea', 'LotConfig_CulDSac', 'LowQualFinSF', 'MSSubClass',
'Neighborhood_BrkSide', 'Neighborhood_Crawfor', 'Neighborhood_NWAmes',
'Neighborhood_NoRidge', 'Neighborhood_NridgHt', 'Neighborhood_Somerst',
'Neighborhood_StoneBr', 'OverallCond', 'OverallQual', 'PoolArea', 'RoofMatl_WdShngl',
'SaleCondition_Normal', 'SaleType_New', 'ScreenPorch', 'TotalBsmtSF', 'WoodDeckSF',
'YearBuilt']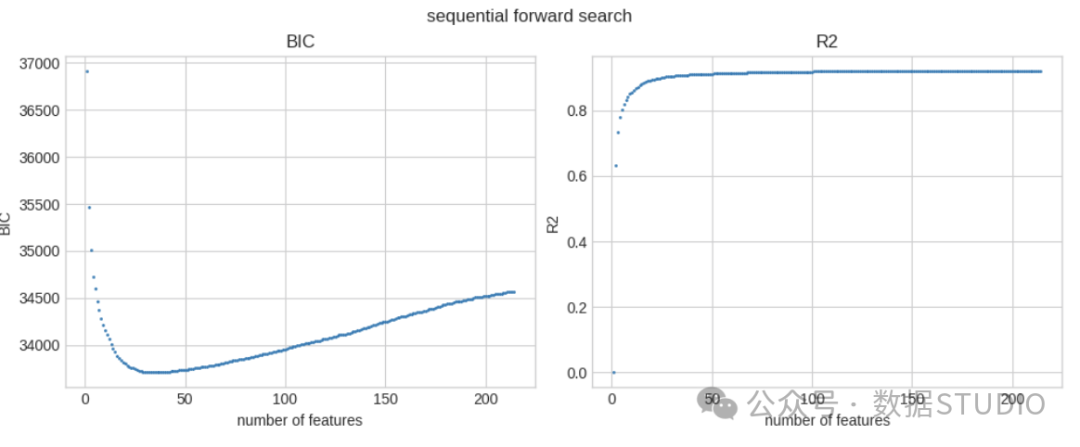
BIC and R-squared for SFS
SFS 的 BIC 和 R 平方
有關實際選擇的特征名稱：
'const', 'BedroomAbvGr', 'BldgType_1Fam', 'BsmtFinSF1',
'Condition1_Norm', 'Condition2_PosN', 'ExterQual_Ex',
'Exterior1st_BrkFace', 'Functional_Sev', 'Functional_Typ',
'GarageArea', 'GrLivArea', 'HeatingQC_Ex', 'KitchenQual_Ex',
'LandContour_HLS', 'LotArea', 'LotConfig_CulDSac', 'LowQualFinSF',
'MSSubClass', 'Neighborhood_BrkSide', 'Neighborhood_Crawfor',
'Neighborhood_NWAmes', 'Neighborhood_NoRidge', 'Neighborhood_NridgHt',
'Neighborhood_Somerst', 'Neighborhood_StoneBr', 'OverallCond',
'OverallQual', 'PoolArea', 'RoofMatl_WdShngl', 'SaleCondition_Normal',
'SaleType_New', 'ScreenPorch', 'TotalBsmtSF', 'WoodDeckSF', 'YearBuilt'協方差矩陣適應演化策略(CMA-ES)
CMA-ES是一種高效的無約束/約束黑箱連續優化的隨機搜索算法。它屬于進化計算的一種,但與傳統的遺傳算法有著明顯區別。
與遺傳算法直接對解個體進行變異和交叉操作不同，CMA-ES在連續域上對多元正態分布模型的參數(均值和協方差矩陣)進行更新迭代，間接實現對潛在解集群的適應性搜索。
算法不需要目標函數的梯度信息，即無需計算導數，因此具有很強的魯棒性，可應用于非線性、非凸、多峰、多模態等各種復雜優化問題。同時，CMA-ES通過自適應策略有效利用樣本信息，在保證全局性的同時提高了收斂速度。
CMA-ES已被廣泛應用于機器學習、計算機視覺、計算生物學等諸多領域，并成為優選的優化算法之一。在Optuna、PyGMO等知名數值優化庫中都有CMA-ES的實現版本。由于算法理論較為復雜，這里只是簡要介紹，可參考文末的擴展閱讀材料進一步學習。
考慮二維 Rastrigin 函數：
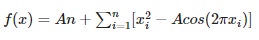Rastrigin 函數
下面的熱圖顯示了該函數的值--顏色越亮表示值越高。該函數的全局最小值位于原點（0，0），但其中有許多局部極值。我們需要通過 CMA-ES 找出全局最小值。
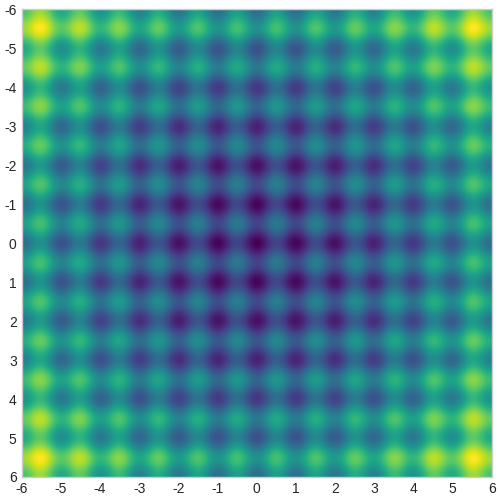Rastrigin 函數熱圖
CMA-ES利用多元正態分布作為基礎。它根據該分布在搜索空間中生成測試點。用戶需要猜測分布的原始均值和標準偏差，然后算法會反復調整這些參數，并在搜索空間中掃描分布，以尋找最佳的目標函數值。以下是測試點的初始分布：
CMA-ES 分布
xi 表示算法在搜索空間中產生的每一步的點集。lambda 是產生的點數。該分布的平均值在每一步中都會更新，最終希望收斂到真正的解決方案。sigma 是分布的標準偏差，即測試點的分布。C 是協方差矩陣，它定義了分布的形狀。根據 C 的值，分布可能是“圓形”，也可能是拉長的橢圓形。改變 C 可以讓CMA-ES進入搜索空間的某些區域，或者避開其他區域。
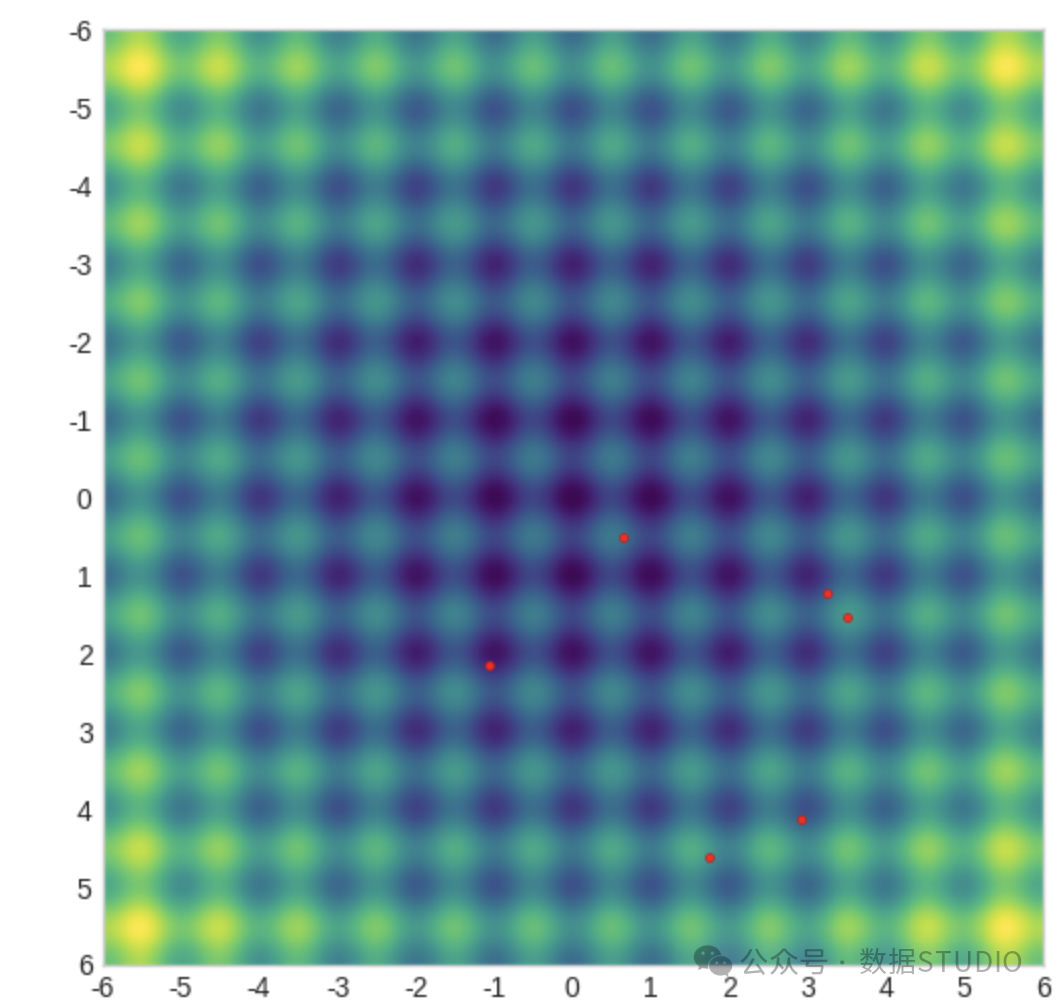第一代測試點
在圖中創建了一個包含6個點的群體，這是優化器選擇的默認群體大小。這是第一步。接下來，算法需要：
- 測算每個點的目標函數（Rastrigin）
- 根據從目標函數中獲得的知識，更新均值、標準差和協方差矩陣，有效地創建一個新的多元正態分布
- 使用新的分布產生一組新的測試點
- 重復這個過程，直到達到某個標準（要么收斂到某個平均值，要么超過最大步數等）。
僅僅更新分布的平均值是非常簡單的。工作原理如下：計算每個測試點的目標函數后，給這些點分配權重，目標值較高的點權重較大，然后根據它們的位置計算出加權和，這就是新的平均值。實際上，CMA-ES（協方差矩陣自適應演化策略）將分布均值向目標值較好的點移動。
更新 CMA-ES 分布均值
如果算法達到真實解決方案，分布的平均值將趨于該解決方案。協方差矩陣將導致分布的形狀發生變化（圓形或橢圓形），這取決于目標函數的地理位置，會向有利的區域擴展，而回避不利的區域。
用于 CMA-ES 特征選擇
二維Rastrigin函數相對簡單，因為它只有2個維度。然而，對于我們的特征選擇問題，我們面臨N=213個維度，并且空間并不是連續的。每個測試點都是一個N維向量，分量的值為"{0, 1}"。換句話說，每個測試點看起來像這樣：1，0，0，1，1，0，......一個二進制向量。除此之外，問題是相同的：我們需要找到使目標函數（即OLS模型的BIC參數）最小化的點或向量。
對于具有 213 個維度和離散取值（0 或 1）的特征選擇問題，您可以考慮使用遺傳算法或者模擬退火算法來尋找最優解。這些算法對于高維度和離散空間的優化問題非常有效。
- 遺傳算法是一種啟發式搜索算法，通過模擬生物進化的過程來搜索最優解。它適用于高維度問題和離散取值空間。
- 模擬退火算法則是一種隨機搜索算法，通過模擬固體退火過程中的原子運動來搜索最優解。它可以通過適當設置的溫度參數來在離散空間中進行搜索。
可以將特征選擇問題建模為一個多維的優化問題，然后使用上述算法來尋找最小化目標函數的解。這些算法可以幫助你在高維度和離散空間中尋找較優的特征子集。
下面是使用 cmaes 庫[3] 進行特征選擇的 CMA-ES 代碼的簡單版本：
def cma_objective(fs):
features_use = ['const'] + [
f for i, f in enumerate(features_select) if fs[i,] == 1
]
lin_mod = sm.OLS(y_cmaes, X_cmaes[features_use], hascnotallow=True).fit()
return lin_mod.bic
X_cmaes = X.copy()
y_cmaes = y.copy()
features_select = [f for f in X_cmaes.columns if f != 'const']
dim = len(features_select)
bounds = np.tile([0, 1], (dim, 1))
steps = np.ones(dim)
optimizer = CMAwM(
mean=np.full(dim, 0.5),
sigma=1 / 6,
bounds=bounds,
steps=steps,
n_max_resampling=10 * dim,
seed=0,
)
max_gen = 100
best_objective_cmaes_small = np.inf
best_sol_raw_cmaes_small = None
for gen in tqdm(range(max_gen)):
solutions = []
for _ in range(optimizer.population_size):
x_for_eval, x_for_tell = optimizer.ask()
value = cma_objective(x_for_eval)
solutions.append((x_for_tell, value))
if value < best_objective_cmaes_small:
best_objective_cmaes_small = value
best_sol_raw_cmaes_small = x_for_eval
optimizer.tell(solutions)
best_features_cmaes_small = [
features_select[i]
for i, val in enumerate(best_sol_raw_cmaes_small.tolist())
if val == 1.0
]
print(f'best objective: {best_objective_cmaes_small}')
print(f'best features: {best_features_cmaes_small}')CMA-ES 優化器的定義涉及對均值和 sigma（標準偏差）進行一些初始猜測。然后，優化器會循環運行多代，創建測試點 x_for_eval ，并根據目標評估其，然后修改分布（均值、sigma、協方差矩陣）等。每個x_for_eval點都是一個二進制向量[1, 1, 1, 0, 0, 1, ...]，用于從數據集中選擇特征。
請注意，這里使用的是 CMAwM() 優化器（帶邊際的 CMA），而不是默認的 CMA()。默認優化器在處理常規連續問題時效果很好，但這里的搜索空間是高維的，只允許兩個離散值（0 和 1）。默認優化器就會卡在這個空間里。CMAwM()擴大了一點搜索空間（而它返回的解仍然是二進制向量），這似乎足以解除它的阻礙。
這段簡單的代碼確實有效，但還遠未達到最佳狀態。下面是一個更復雜、更優化的版本，它能更快地找到更好的解。
def cma_objective(fs):
features_use = ['const'] + [
f for i, f in enumerate(features_select) if fs[i,] == 1
]
lin_mod = sm.OLS(y_cmaes, X_cmaes[features_use], hascnotallow=True).fit()
return lin_mod.bic
# copy the original dataframes into local copies, once
X_cmaes = X.copy()
y_cmaes = y.copy()
rs = np.random.RandomState(seed=0)
features_select = [f for f in X_cmaes.columns if f != 'const']
n_features = len(features_select)
cma_bounds = np.tile([0, 1], (n_features, 1))
cma_steps = np.ones(n_features)
n_max_resampling = 10 * n_features
mean = np.full(n_features, 0.5)
sigma = 1 / 6
pop_size = 4 + math.floor(3 * math.log(n_features))
margin = 1 / (n_features * pop_size)
optimizer = CMAwM(
mean=mean,
sigma=sigma,
bounds=cma_bounds,
steps=cma_steps,
n_max_resampling=n_max_resampling,
seed=0,
population_size=pop_size,
margin=margin,
)
gen_max = 1000
best_objective_cmaes = np.inf
best_generation_cmaes = 0
best_sol_raw_cmaes = None
history_values_cmaes = np.full((gen_max,), np.nan)
history_values_best_cmaes = np.full((gen_max,), np.nan)
time_to_best_cmaes = np.inf
objective_runs_cmaes = 0
solutions_avg = np.full((gen_max, n_features), np.nan)
n_jobs = os.cpu_count()
iterator = tqdm(range(gen_max), desc='generation')
t_start_cmaes = time.time()
for generation in iterator:
best_value_gen = np.inf
# solutions fed back to the optimizer
solutions_float = []
# binary-truncated solutions - the yes/no answers we're looking for
solutions_binary = np.full((pop_size, n_features), np.nan)
vals = np.full((pop_size,), np.nan)
for i in range(pop_size):
# re-seeding the RNG is very important
# otherwise CMA-ES gets stuck in local extremes
seed = rs.randint(1, 2**16) + generation
optimizer._rng.seed(seed)
fs_for_eval, fs_for_tell = optimizer.ask()
solutions_binary[i,] = fs_for_eval
value = cma_objective(fs_for_eval)
objective_runs_cmaes += 1
vals[i] = value
solutions_float.append((fs_for_tell, value))
optimizer.tell(solutions_float)
solutions_avg[generation,] = solutions_binary.mean(axis=0)
best_value_gen = vals.min()
t_end_loop_cmaes = time.time()
if best_value_gen < best_objective_cmaes:
best_objective_cmaes = best_value_gen
best_generation_cmaes = generation
best_sol_raw_cmaes = solutions_binary[np.argmin(vals),]
time_to_best_cmaes = t_end_loop_cmaes - t_start_cmaes
print(
f'gen: {best_generation_cmaes:5n}, new best objective: {best_objective_cmaes:.4f}'
)
history_values_cmaes[generation] = best_value_gen
history_values_best_cmaes[generation] = best_objective_cmaes
if optimizer.should_stop():
print(f'Optimizer decided to stop.')
iterator.close()
break
if os.path.isfile('break'):
# to gracefully break the loop, manually create a file called 'break'
print(f'Found break file, stopping now.')
iterator.close()
break
gen_completed_cmaes = generation
best_features_cmaes = [
features_select[i]
for i, val in enumerate(best_sol_raw_cmaes.tolist())
if val == 1.0
]
print(f'best objective: {best_objective_cmaes}')
print(f'best generation: {best_generation_cmaes}')
print(f'objective runs: {objective_runs_cmaes}')
print(f'time to best: {time_to_best_cmaes:.3f} sec')
print(f'best features: {best_features_cmaes}')
cma_mv_df = pd.DataFrame(solutions_avg, columns=features_select).iloc[
: gen_completed_cmaes + 1
]
if gen_completed_cmaes > 20:
x_ticks = list(
range(0, gen_completed_cmaes, round(gen_completed_cmaes / 20))
)
else:
x_ticks = list(range(0, gen_completed_cmaes))
if x_ticks[-1] != gen_completed_cmaes:
x_ticks.append(gen_completed_cmaes)
fig, ax = plt.subplots(
2,
1,
sharex=True,
height_ratios=[20, 1],
figsize=(12, 45),
layout='constrained',
)
sns.heatmap(
cma_mv_df.T,
vmin=0.0,
vmax=1.0,
cmap='viridis',
cbar=True,
cbar_kws={'fraction': 0.01, 'anchor': (0.0, 1.0)},
ax=ax[0],
)
ax[0].axvline(x=best_generation_cmaes, color='C7')
ax[0].tick_params(axis='both', reset=True)
ax[0].set_xticks(x_ticks)
ax[0].set_xticklabels(x_ticks)
ax[0].set_title('Population average of feature selector values')
ax[0].set_xlabel('generation')
ax[1].scatter(
range(gen_completed_cmaes + 1),
history_values_cmaes[: gen_completed_cmaes + 1],
s=1,
label='current value',
)
ax[1].plot(
range(gen_completed_cmaes + 1),
history_values_best_cmaes[: gen_completed_cmaes + 1],
color='C1',
label='best value',
)
ax[1].vlines(
x=best_generation_cmaes,
ymin=history_values_cmaes[: gen_completed_cmaes + 1].min(),
ymax=history_values_cmaes[: gen_completed_cmaes + 1].max(),
colors='C7',
)
ax[1].tick_params(axis='both', reset=True)
ax[1].legend()
ax[1].set_title('Objective value')
ax[1].set_xlabel('generation')
fig.suptitle('CMA-ES')
fig.savefig('cmaes-performance.png')
fig.show()best objective: 33703.070530508514
best generation: 921
objective runs: 20000
time to best: 48.326 sec
best features: ['BedroomAbvGr', 'BldgType_1Fam', 'BsmtFinSF1', 'Condition1_Norm',
'Condition2_PosN', 'ExterQual_Ex', 'Exterior1st_BrkFace', 'Functional_Sev',
'Functional_Typ', 'GarageCars', 'GrLivArea', 'HeatingQC_Ex', 'KitchenQual_Ex',
'LandContour_HLS', 'LotArea', 'LowQualFinSF', 'Neighborhood_BrkSide',
'Neighborhood_Crawfor', 'Neighborhood_NWAmes', 'Neighborhood_NoRidge',
'Neighborhood_NridgHt', 'Neighborhood_Somerst', 'Neighborhood_StoneBr', 'OverallCond',
'OverallQual', 'PoolArea', 'RoofMatl_WdShngl', 'SaleCondition_Normal', 'SaleType_New',
'ScreenPorch', 'TotalBsmtSF', 'WoodDeckSF', 'YearBuilt']下圖顯示了復雜、優化的 CMA-ES 代碼搜索最佳解決方案的歷史。熱圖顯示了每一代中每種功能的流行程度（更亮 = 更流行）。可以看到，有些特征總是非常流行，而另一些則很快過時，還有一些則是后來才 “發現 ”的。根據這個問題的參數，優化器選擇的群體大小為 20 個點（個體），因此特征流行度是這 20 個點的平均值。
上下滑動查看更多CMA-ES 優化歷史這些是經過優化的 CMA-ES 代碼的主要統計信息：
best objective: 33703.070530508514
best generation: 921
objective runs: 20000
time to best: 48.326 sec與 SFS 相比，它能找到更好（更小）的目標值，調用目標函數的次數更少（20k），所用時間也差不多。從所有指標來看，這都是比 SFS 的凈收益。
同樣，特征選擇前的基準 BIC 為
baseline BIC: 34570.166173470934順便提一句：在研究了傳統優化算法（遺傳算法、模擬退火等）之后，CMA-ES 給我帶來了驚喜。它幾乎沒有超參數，計算量小，只需要少量個體（點）來探索搜索空間，而且性能相當不錯。如果你需要解決優化問題，值得把它放在你的工具箱里。
參考資料
[1]Kaggle: https://www.kaggle.com/c/house-prices-advanced-regression-techniques/data
[2]mlxtend 庫: https://rasbt.github.io/mlxtend/
[3]cmaes 庫: https://github.com/CyberAgentAILab/cmaes
