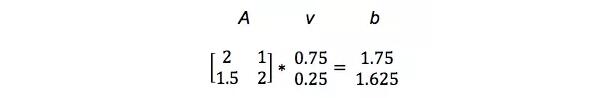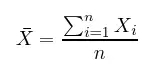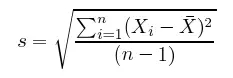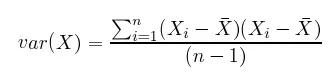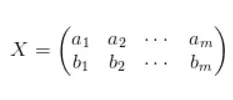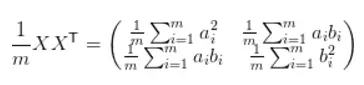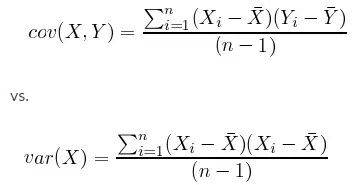本文先簡要明了地介紹了特征向量和其與矩陣的關系，然后再以其為基礎解釋協方差矩陣和主成分分析法的基本概念，***我們結合協方差矩陣和主成分分析法實現數據降維。本文不僅僅是從理論上闡述各種重要概念，同時***還一步步使用 Python 實現數據降維。

首先本文的特征向量是數學概念上的特征向量，并不是指由輸入特征值所組成的向量。數學上，線性變換的特征向量是一個非簡并的向量，其方向在該變換下不變。該向量在此變換下縮放的比例稱為特征值。一個線性變換通常可以由其特征值和特征向量完全描述。如果我們將矩陣看作物理運動，那么最重要的就是運動方向(特征向量)和速度(特征值)。因為物理運動只需要方向和速度就可以描述，同理矩陣也可以僅使用特征向量和特征值描述。

其實在線性代數中，矩陣就是一個由各種標量或變量構成的表格，它和 Excel 表格并沒有什么本質上的區別。只不過數學上定義了一些矩陣間的運算，矩陣運算的法則和實際內部的值并沒有什么關系，只不過定義了在運算時哪些位置需要進行哪些操作。因為矩陣相當于定義了一系列運算法則的表格，那么其實它就相當于一個變換，這個變換(物理運動)可以由特征向量(方向)和特征值(速度)完全描述出來。

線性變換

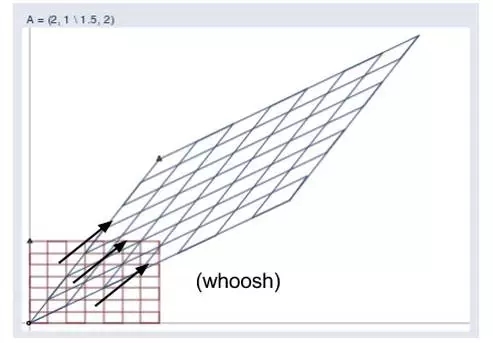
在解釋線性變換前，我們需要先了解矩陣運算到底是什么。因為我們可以對矩陣中的值統一進行如加法或乘法等運算，所以矩陣是十分高效和有用的。如下所示，如果我們將向量 v 左乘矩陣 A，我們就會得到新的向量 b，也即可以表述說矩陣 A 對輸入向量 v 執行了一次線性變換，且線性變換結果為 b。因此矩陣運算 Av = b 就代表向量 v 通過一個變換(矩陣 A)得到向量 b。下面的實例展示了矩陣乘法(該類型的乘法稱之為點積)是怎樣進行的：

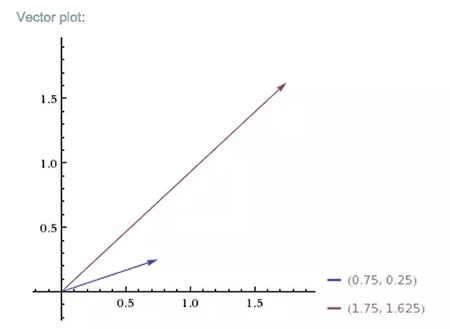
所以矩陣 A 將向量 v 變換為向量 b。下圖展示了矩陣 A 如何將更短更低的向量 v 映射到更長更高的向量 b：

我們可以饋送其他正向量到矩陣 A 中，每一個饋送的向量都會投影到新的空間中且向右邊變得更高更長。

假定所有的輸入向量 V 可以排列為一個標準表格，即：

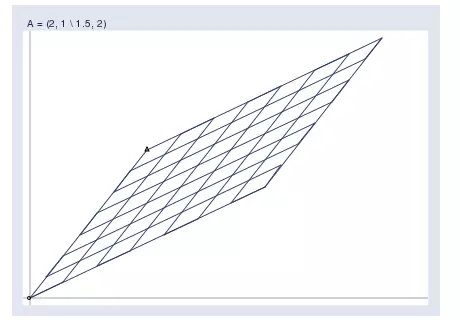
而矩陣可以將所有的輸入向量 V 投影為如下所示的新空間，也即所有輸出向量組成的 B：

下圖可以看到輸入向量空間和輸出向量空間的關系，

如果假設矩陣就是一陣風，它通過有形的力量得出可見的結果。而這一陣風所吹向的方向就是特征向量，因此特征向量就表明矩陣所要變換的方向。

如上圖所示，特征向量并不會改變方向，它已經指向了矩陣想要將所有輸入向量都推向的方向。因此，特征向量的數學定義為：存在非零矩陣 A 和標量λ，若有向量 x 且滿足以下關系式，那么 x 就為特征向量、λ為特征值。

特征向量同樣是線性變換的不變軸，所有輸入向量沿著這條軸壓縮或延伸。線性變換中的線性正是表明了這種沿直線軸進行變換的特性，一般來說幾階方陣就有幾個特征向量，如 3*3 矩陣有 3 個特征向量，n 階方陣有 n 個特征向量，每一個特征向量表征一個維度上的線性變換方向。

因為特征向量提取出了矩陣變換的主要信息，因此它在矩陣分解中十分重要，即沿著特征向量對角化矩陣。因為這些特征向量表征著矩陣的重要特性，所以它們可以執行與深度神經網絡中自編碼器相類似的任務。引用 Yoshua Bengio 的話來說：

許多數學對象可以通過分解為更基礎的組成部分而有更好的理解，因為我們會發現它們的一些廣泛性屬性，而不是我們選擇表征它們的特性。例如整數可以分解為質因數，雖然我們表征整數的方式會因為采用二進制還是十進制而改變，但整數總可以由幾個質因數表示(如 12=2 × 2 × 3)，因此這種分解的性質正好是我們所需要的穩定性質。

我們可以分解一個整數為質因數而得到其自然屬性，同樣我們也可以分解矩陣以得到它的功能性屬性，并且這種屬性信息在矩陣表示為多組元素的陣列下是不明顯的。矩陣分解最常見的是特征分解(eigen-decomposition)，即我們將矩陣分解為一系列的特征向量和特征值。

主成分分析(PCA)

PCA 是一種尋找高維數據(圖像等)模式的工具。機器學習實踐上經常使用 PCA 對輸入神經網絡的數據進行預處理。通過聚集、旋轉和縮放數據，PCA 算法可以去除一些低方差的維度而達到降維的效果，這樣操作能提升神經網絡的收斂速度和整體效果。

為了進一步了解 PCA 算法，我們還需要定義一些基本的統計學概念，即均值、標準差、方差和協方差。

樣本均值可簡單的表示為所有樣本 X 的平均值，如下所示樣本均值表示為：

樣本標準差即樣本方差的平方根。即每一樣本點到樣本均值之間的平均距離。n 個樣本的方差卻只除以 n-1 是因為樣本只是真實分布的估計量，樣本方差也只是真實方差的估計量。在大學課本概率論和數理統計中有證明，如果除以 n(2 階中心矩)，那么樣本方差是真實方差的一致性估計，但并不是無偏估計，也就是樣本方差存在系統偏差。因此我們需要對 2 階中心矩進行調整以消除系統偏差。如下所示，樣本的標準差 s 和方差 var(X) 都是無偏估計：

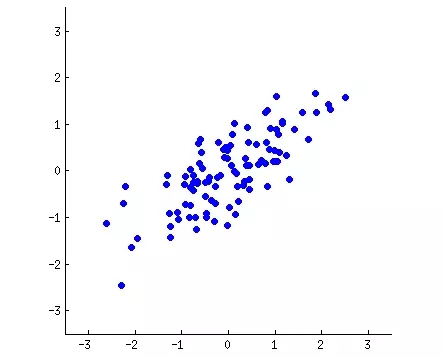
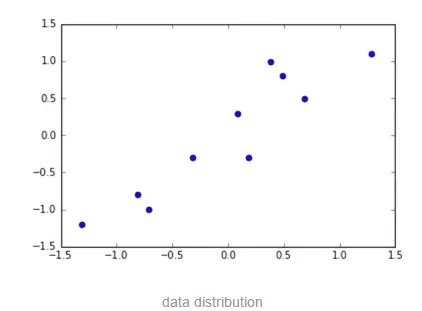
因為樣本標準差和方差都是先求距離的平方再求平方根，因此距離一定是正數且不會抵消。假設我們有如下數據點(散點圖)：

PCA 如線性回歸那樣會嘗試構建一條可解釋性的直線貫穿所有數據點。每一條直線表示一個「主成分」或表示自變量和因變量間的關系。數據的維度數就是主成分的數量，也即每一個數據點的特征維度。PCA 的作用就是分析這些特征，并選出最重要的特征。PCA 本質上是將方差***的方向作為主要特征，并且在各個正交方向上將數據「去相關」，也就是讓它們在不同正交方向上沒有相關性。通常我們認為信息具有較大的方差，而噪聲有較小的方差，信噪比就是信號與噪聲的方差比，所以我們希望投影后的數據方差越大越好。因此我們認為，***的 k 維特征是將 n 維樣本點轉換為 k 維后，每一維上的樣本方差都很大。

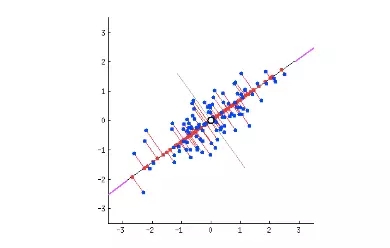
如下圖所示，***個主成分以直線(紅色)的形式將散點圖分為兩邊，并且它是保留了***方差的。因為投影到這條直線(紅色)上數據點離均值(空心點)有***的方差，即所有藍點到灰色線的平均距離為***方差，所以這一個主成分將保留最多的信息。

如上所示，假設第二個主成分為垂直于紅線(***個主成分)的灰色線。當數據點投影到第二個主成分上時，它們離樣本均值(空心點)的方差卻非常小，即數據點到紅色線的平均距離。所以紅色線是***的主成分。

協方差矩陣

前面我們已經了解矩陣其實就是一種將某個向量變換為另一個的方法，另外我們也可以將矩陣看作作用于所有數據并朝向某個方向的力。同時我們還知道了變量間的相關性可以由方差和協方差表達，并且我們希望保留***方差以實現***的降維。因此我們希望能將方差和協方差統一表示，并且兩者均可以表示為內積的形式，而內積又與矩陣乘法密切相關。因此我們可以采用矩陣乘法的形式表示。若輸入矩陣 X 有兩個特征 a 和 b，且共有 m 個樣本，那么有：

如果我們用 X 左乘 X 的轉置，那么就可以得出協方差矩陣：

這個矩陣對角線上的兩個元素分別是兩特征的方差，而其它元素是 a 和 b 的協方差。兩者被統一到了一個矩陣的，因此我們可以利用協方差矩陣描述數據點之間的方差和協方差，即經驗性地描述我們觀察到的數據。

尋找協方差矩陣的特征向量和特征值就等價于擬合一條能保留***方差的直線或主成分。因為特征向量追蹤到了主成分的方向，而***方差和協方差的軸線表明了數據最容易改變的方向。根據上述推導，我們發現達到優化目標就等價于將協方差矩陣對角化：即除對角線外的其它元素化為 0，并且在對角線上將特征值按大小從上到下排列。協方差矩陣作為實對稱矩陣，其主要性質之一就是可以正交對角化，因此就一定可以分解為特征向量和特征值。

當協方差矩陣分解為特征向量和特征值之后，特征向量表示著變換方向，而特征值表示著伸縮尺度。在本例中，特征值描述著數據間的協方差。我們可以按照特征值的大小降序排列特征向量，如此我們就按照重要性的次序得到了主成分排列。

對于 2 階方陣，一個協方差矩陣可能如下所示：

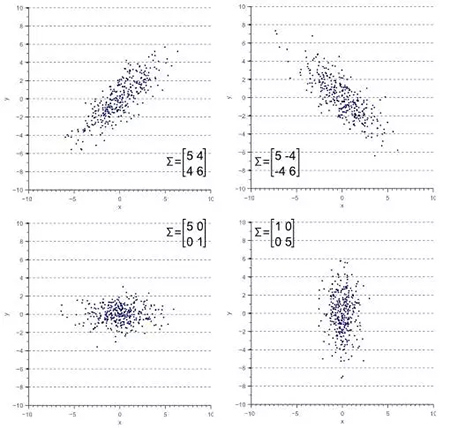
在上面的協方差矩陣中，1.07 和 0.64 分別代表變量 x 和變量 y 的方差，而副對角線上的 0.63 代表著變量 x 和 y 之間的協方差。因為協方差矩陣為實對稱矩陣(即 Aij=Aji)，所以其必定可以通過正交化相似對角化。因為這兩個變量的協方差為正值，所以這兩個變量的分布成正相關性。如下圖所示，如果協方差為負值，那么變量間就成負相關性。

注意如果變量間的協方差為零，那么變量是沒有相關性的，并且也沒有線性關系。因此，如果兩個變量的協方差越大，相關性越大，投影到主成分后的損失就越小。我們同時可以考慮協方差和方差的計算式而了解他們的關系：

計算協方差的優處在于我們可以通過協方差的正值、負值或零值考察兩個變量在高維空間中相互關系。總的來說，協方差矩陣定義了數據的形狀，協方差決定了沿對角線對稱分布的強度，而方差決定了沿 x 軸或 y 軸對稱分布的趨勢。

基變換

因為協方差矩陣的特征向量都是彼此正交的，所以變換就相當于將 x 軸和 y 軸兩個基軸換為主成分一個基軸。也就是將數據集的坐標系重新變換為由主成分作為基軸的新空間，當然這些主成分都保留了***的方差。

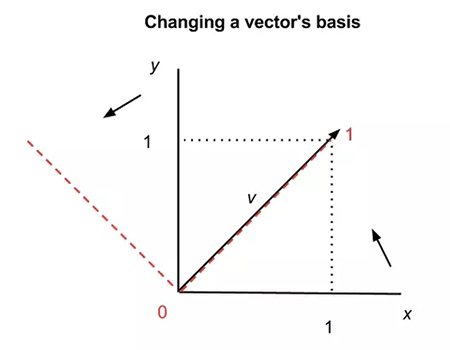
我們上面所述的 x 軸和 y 軸稱之為矩陣的基，即矩陣所有的值都是在這兩個基上度量而來的。但矩陣的基是可以改變的，通常一組特征向量就可以組成該矩陣一組不同的基坐標，原矩陣的元素可以在這一組新的基中表達。

在上圖中，我們展示了相同向量 v 如何在不同的坐標系中有不同的表達。黑色實線代表 x-y 軸坐標系而紅色虛線是另外一個坐標系。在***個坐標系中 v = (1,1)，而在第二個坐標系中 v = (1,0)。因此矩陣和向量可以在不同坐標系中等價變換。在數學上，n 維空間并沒有唯一的描述，所以等價轉換矩陣的基也許可以令問題更容易解決。

***我們簡單地總結一下 PCA 算法的基本概念和步驟：

首先我們得理解矩陣就相當于一個變換，變換的方向為特征向量，變換的尺度為特征值。PCA 的本質是將方差***的方向作為主要特征，并且在各個正交方向上將數據「去相關」，即讓它們在不同正交方向上沒有相關性。所以我們希望將最相關的特征投影到一個主成分上而達到降維的效果，投影的標準是保留***方差。而在實際操作中，我們希望計算特征之間的協方差矩陣，并通過對協方差矩陣的特征分解而得出特征向量和特征值。如果我們將特征值由大到小排列，相對應的特征向量所組成的矩陣就是我們所需降維后的數據。下面我們將一步步實現 PCA 算法。

輸入數據：

import numpy as np 
x=np.array([2.5,0.5,2.2,1.9,3.1,2.3,2,1,1.5,1.1]) 
y=np.array([2.4,0.7,2.9,2.2,3,2.7,1.6,1.1,1.6,0.9]) 

歸一化數據：

mean_x=np.mean(x) 
mean_y=np.mean(y) 
scaled_x=x-mean_x 
scaled_y=y-mean_y 
data=np.matrix([[scaled_x[i],scaled_y[i]] for i in range(len(scaled_x))]) 

繪制散點圖查看數據分布：

import matplotlib.pyplot as plt 
plt.plot(scaled_x,scaled_y,'o') 

求協方差矩陣：

cov=np.cov(scaled_x,scaled_y) 

求協方差矩陣的特征值和特征向量：

eig_val, eig_vec = np.linalg.eig(cov) 

求出特征向量后，我們需要選擇降維后的數據維度 k(n 維數據降為 k 維數據)，但我們的數據只有兩維，所以只能降一維：

eig_pairs = [(np.abs(eig_val[i]), eig_vec[:,i]) for i in range(len(eig_val))] 
eig_pairs.sort(reverse=True) 
feature=eig_pairs[0][1] 

轉化得到降維后的數據：

new_data_reduced=np.transpose(np.dot(feature,np.transpose(data)) 

原文：

https://deeplearning4j.org/eigenvector#a-beginners-guide-to-eigenvectors-pca-covariance-and-entropy

【本文是51CTO專欄機構“機器之心”的原創譯文，微信公眾號“機器之心( id: almosthuman2014)”】

 

戳這里，看該作者更多好文