本文經計算機視覺研究院公眾號授權轉載，轉載請聯系出處。

論文地址：https://arxiv.org/pdf/2111.13824.pdf

項目代碼：https://github.com/megvii-research/FQ-ViT

01 總  述

Transformer 是現在火熱的AIGC預訓練大模型的基礎，而ViT(Vision Transformer)是真正意義上將自然語言處理領域的Transformer帶到了視覺領域。從Transformer的發展歷程就可以看出，從Transformer的提出到將Transformer應用到視覺，其實中間蟄伏了三年的時間。而從將Transformer應用到視覺領域(ViT)到AIGC的火爆也差不多用了兩三年。其實AIGC的火爆，從2022年下旬就開始有一些苗條，那時就逐漸有一些AIGC好玩的算法放出來，而到現在，AIGC好玩的項目真是層出不窮。

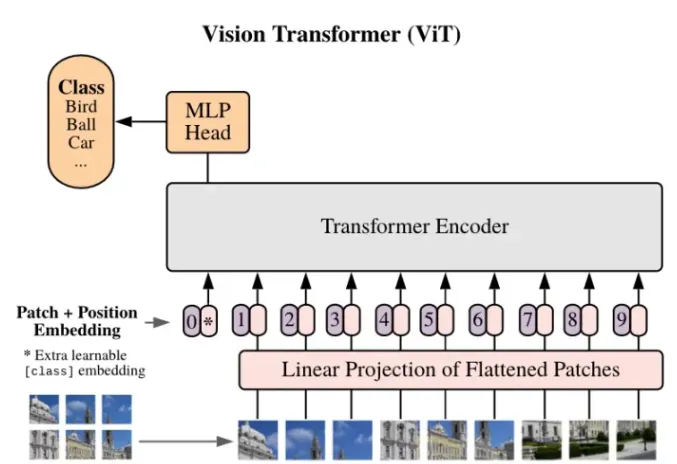
隨著近兩年來對視覺Transformer模型（ViT）的深入研究，ViT的表達能力不斷提升，并已經在大部分視覺基礎任務 (分類，檢測，分割等) 上實現了大幅度的性能突破。然而，很多實際應用場景對模型實時推理的能力要求較高，但大部分輕量化ViT仍無法在多個部署場景 （GPU，CPU，ONNX，移動端等）達到與輕量級CNN（如MobileNet） 相媲美的速度。

因此，重新審視了ViT的2個專屬模塊，并發現了退化原因如下：

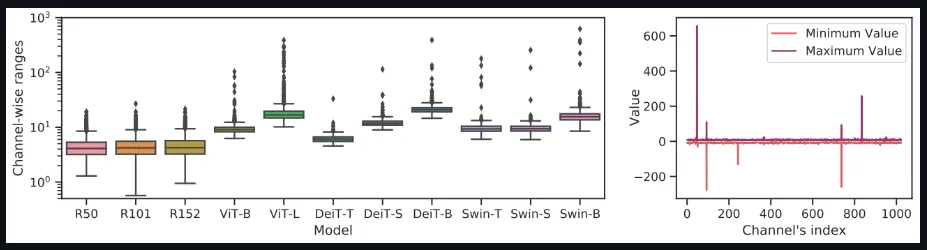
• 研究者發現LayerNorm輸入的通道間變化嚴重，有些通道范圍甚至超過中值的40倍。傳統方法無法處理如此大的激活波動，這將導致很大的量化誤差
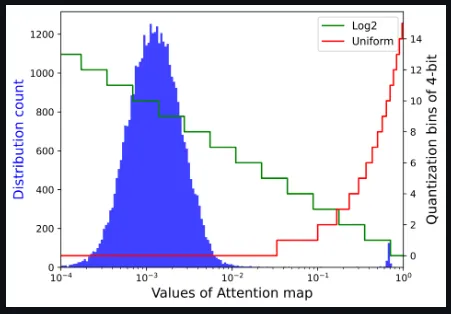
• 還發現注意力圖的值具有極端的不均勻分布，大多數值聚集在0～0.01之間，少數高注意力值接近1

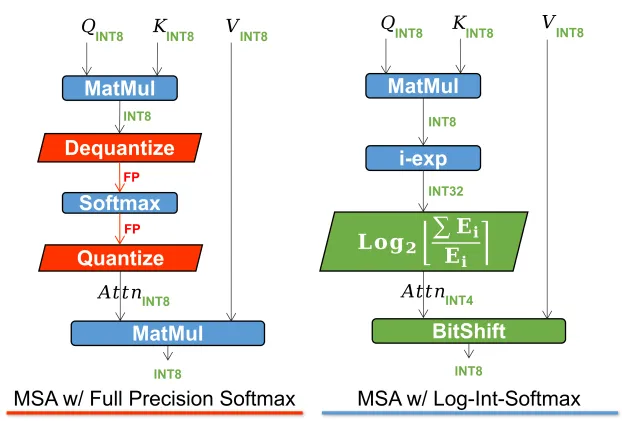
基于以上分析，研究者提出了Power-of-Two Factor（PTF）來量化LayerNorm的輸入。通過這種方式，量化誤差大大降低，并且由于Bit-Shift算子，整體計算效率與分層量化的計算效率相同。此外還提出了Log Int Softmax（LIS），它為小值提供了更高的量化分辨率，并為Softmax提供了更有效的整數推理。結合這些方法，本文首次實現了全量化Vision Transformer的訓練后量化。

02 新框架

下面的這兩張圖表明，與CNN相比，視覺轉換器中存在嚴重的通道間變化，這導致了分層量化的不可接受的量化誤差。

首先解釋網絡量化符號。假設量化位寬為b，量化器Q（X|b）可以公式化為將浮點數X∈R映射到最近量化倉的函數：

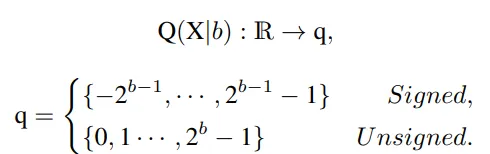
Uniform Quantization

Uniform Quantization在大多數硬件平臺上都得到了很好的支持。它的量化器Q（X|b）可以定義為：

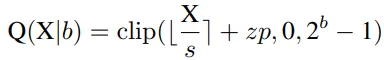
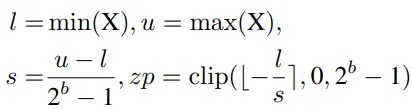
其中s（標度）和zp（零點）是由X的下界l和上界u確定的量化參數，它們通常是最小值和最大值。

Log2 Quantization

Log2 Quantization將量化過程從線性變化轉換為指數變化。其量化器Q（X|b）可定義為:

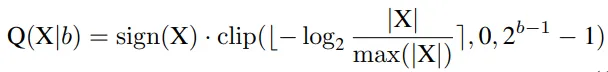
為了實現完全量化的視覺變換器，研究者對所有模塊進行量化，包括Conv、Linear、MatMul、LayerNorm、Softmax等。特別是，對Conv、線性和MatMul模塊使用均勻的Min-Max量化，對LayerNor和Softmax使用以下方法。

Power-of-Two Factor for LayerNorm Quantization

在推理過程中，LayerNorm計算每個正向步驟中的統計量μX，σX，并對輸入X進行歸一化。然后，仿射參數γ，β將歸一化輸入重新縮放為另一個學習分布。

如剛開始解釋分析一樣，與神經網絡中常用的BatchNorm不同，LayerNorm由于其動態計算特性，無法折疊到前一層，因此必須單獨量化它。然而，在對其應用訓練后量化時觀察到顯著的性能下降。查看LayerNorm層的輸入，發現存在嚴重的通道間變化。

研究者提出了一種簡單而有效的層范數量化方法，即Power-of-Two Factor（PTF）。PTF的核心思想是為不同的信道配備不同的因子，而不是不同的量化參數。給定量化位寬b，輸入活動X∈RB×L×C，逐層量化參數s，zp∈R1，以及PTFα∈NC，則量化活動XQ可以公式化為：

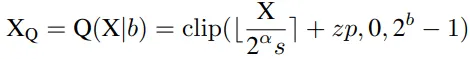
其中部分參數如下：

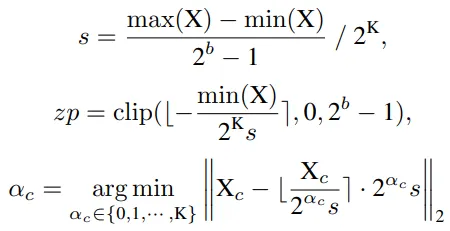
Softmax quantized with Log-Int-Softmax (LIS)

注意圖的存儲和計算是變壓器結構的瓶頸，因此研究者希望將其量化到極低的位寬（例如4位）。然而，如果直接實現4位均勻量化，則會出現嚴重的精度退化。研究者觀察到分布集中在Softmax輸出的一個相當小的值上，而只有少數異常值具有接近1的較大值。基于以下可視化，對于具有密集分布的小值區間，Log2保留了比均勻更多的量化區間。

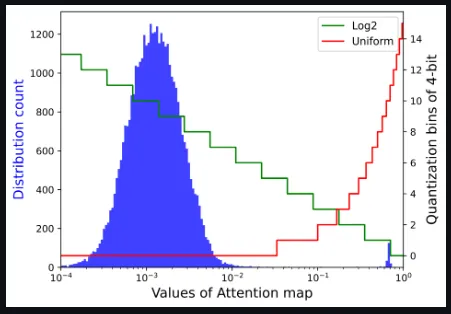
將Log2量化與i-exp（i-BERT提出的指數函數的多項式近似）相結合，提出了LIS，這是一個僅整數、更快、低功耗的Softmax。

整個過程如下所示。

03 實驗&可視化

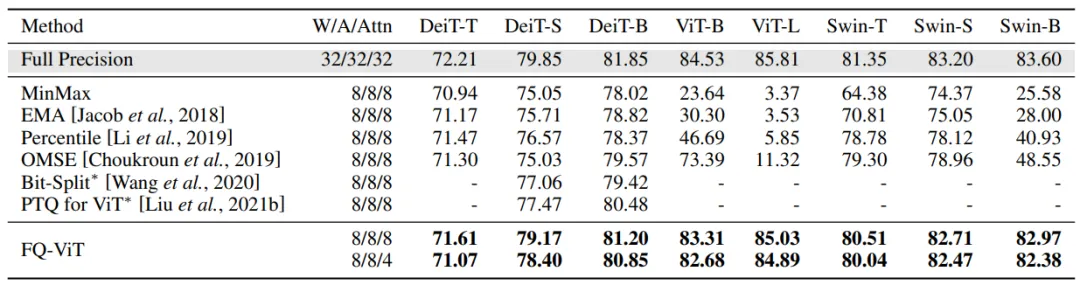
Comparison of the top-1 accuracy with state-of-the-art methods on ImageNet dataset

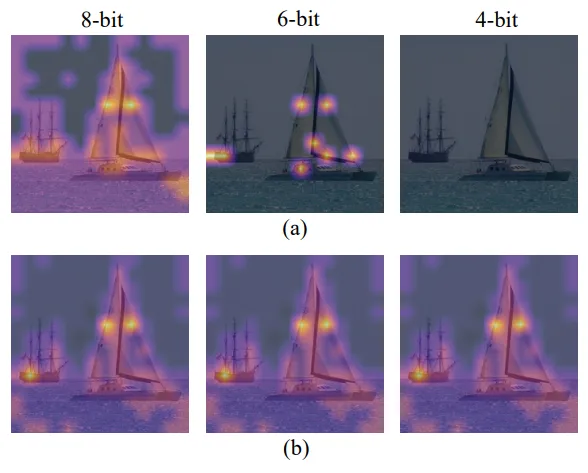
將注意力圖可視化，以查看均勻量化和LIS之間的差異，如上圖所示。當兩者都使用8位時，均勻量化集中在高激活區域，而LIS在低激活區域保留更多紋理，這保留了注意力圖的更多相對秩。在8位的情況下，這種差異不會產生太大的差異。然而，當量化到較低的位寬時，如6位和4位的情況所示，均勻量化會急劇退化，甚至使所有關注區域失效。相反，LIS仍然表現出類似于8位的可接受性能。

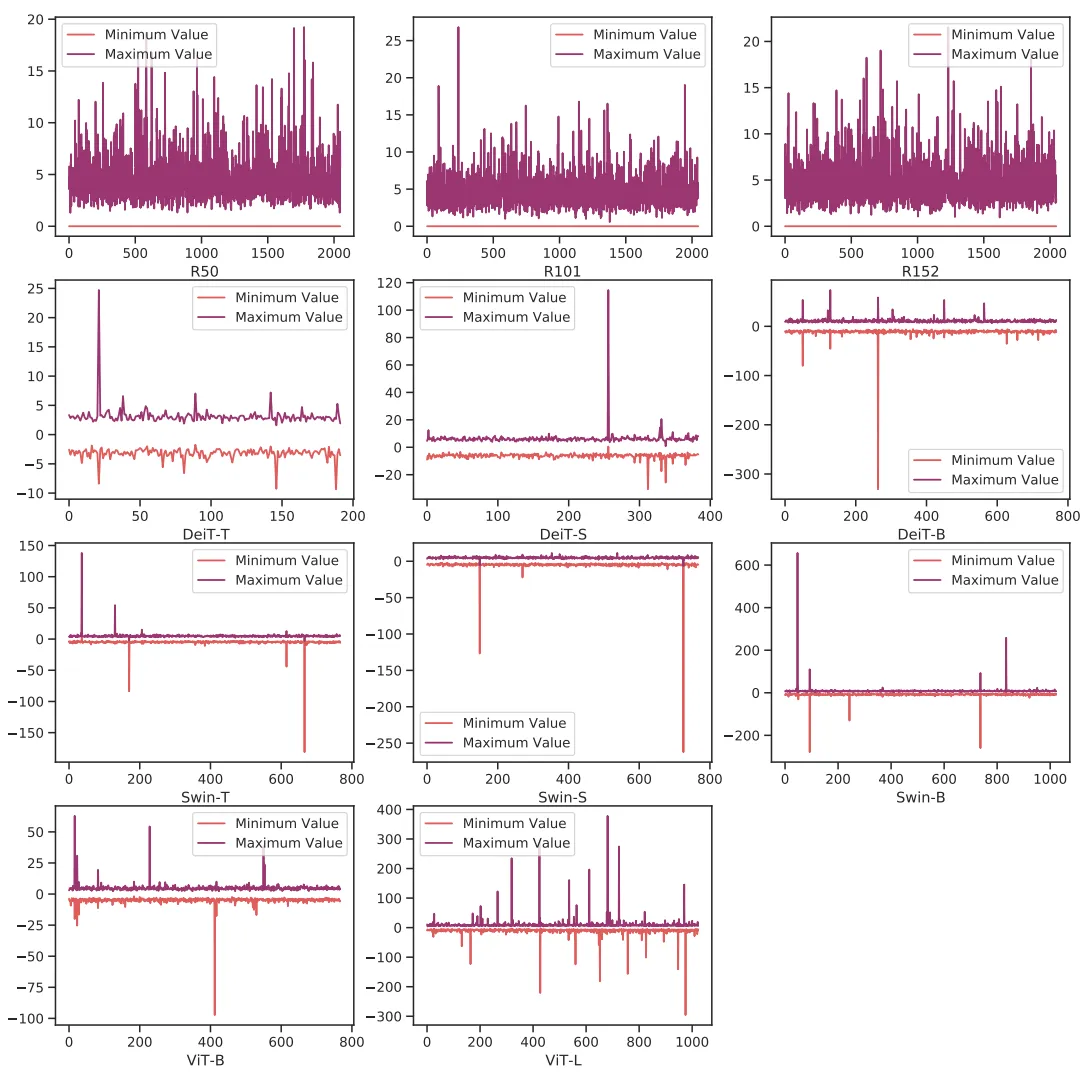
Channel-wise minimum and maximum values of Vision Transformers and ResNets