如何讓等變神經網絡可解釋性更強?試試將它分解成「簡單表示」
神經網絡是一種靈活且強大的函數近似方法。而許多應用都需要學習一個相對于某種對稱性不變或等變的函數。圖像識別便是一個典型示例 —— 當圖像發生平移時,情況不會發生變化。等變神經網絡(equivariant neural network)可為學習這些不變或等變函數提供一個靈活的框架。
而要研究等變神經網絡,可使用表示論(representation theory)這種數學工具。(請注意,「表示」這一數學概念不同于機器學習領域中的「表征」的典型含義。本論文僅使用該術語的數學意義。)
近日,Joel Gibson、Daniel Tubbenhauer 和 Geordie Williamson 三位研究者對等變神經網絡進行了探索,并研究了分段線性表示論在其中的作用。

- 論文標題:Equivariant neural networks and piecewise linear representation theory
- 論文地址:https://arxiv.org/pdf/2408.00949
在表示論中,簡單表示(simple representation)是指該理論的不可約簡的原子。在解決問題時,表示論的一個主要策略是將該問題分解成簡單表示,然后分別基于這些基本片段研究該問題。但對等變神經網絡而言,這一策略并不奏效:它們的非線性性質允許簡單表示之間發生互動,而線性世界無法做到這一點。
但是,該團隊又論證表明:將等變神經網絡的層分解成簡單表示依然能帶來好處。然后很自然地,他們又進一步研究了簡單表示之間的分段線性映射和分段線性表示論。具體來說,這種分解成簡單表示的過程能為神經網絡的層構建一個新的基礎,這是對傅立葉變換的泛化。
該團隊表示:「我們希望這種新基礎能為理解和解讀等變神經網絡提供一個有用的工具。」
該論文證明了什么?
在介紹該論文的主要結果之前,我們先來看一個簡單卻非平凡的示例。
以一個小型的簡單神經網絡為例:
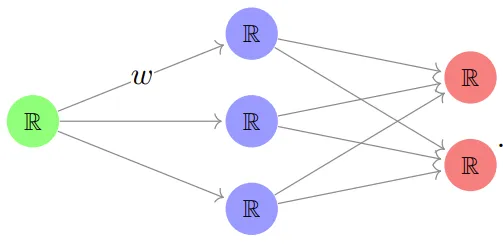
其中每個節點都是 ? 的一個副本,每個箭頭都標記了一個權重 w,并且層之間的每個線性映射的結果都由一個非線性激活函數 ?? 組成,然后再進入下一層。
為了構建等變神經網絡,可將 ? 和 w 替換成具有更多對稱性的更復雜對象。比如可以這樣替換:

其可被描述為:
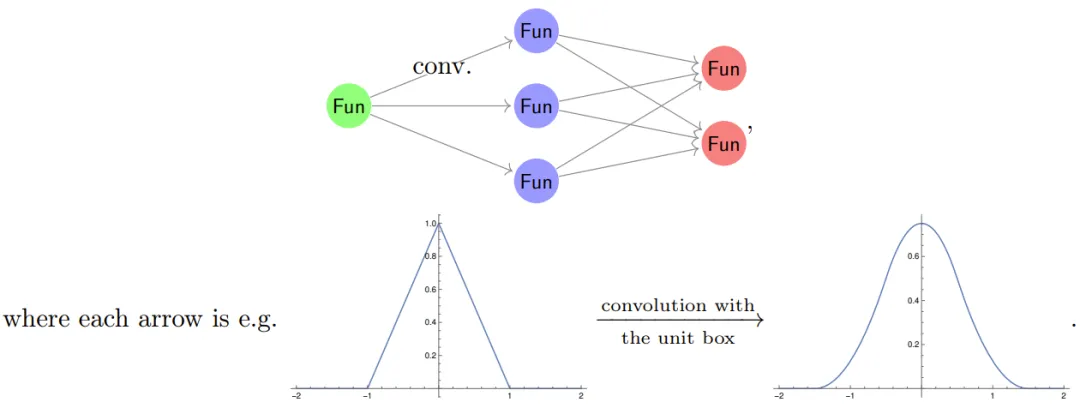
不過,要想在計算機上真正實現這個結構,卻根本不可能,但這里先忽略這一點。
現在暫時假設函數是周期性的,周期為 2π。當用傅里葉級數展開神經網絡時,我們很自然就會問發生了什么。在傅里葉理論中,卷積算子會在傅里葉基中變成對角。因此,為了理解信號流過上述神經網絡的方式,還需要理解激活函數在基頻上的工作方式。
一個基本卻關鍵的觀察是:??(sin (x)) 的傅里葉級數僅涉及較高共振頻率的項:
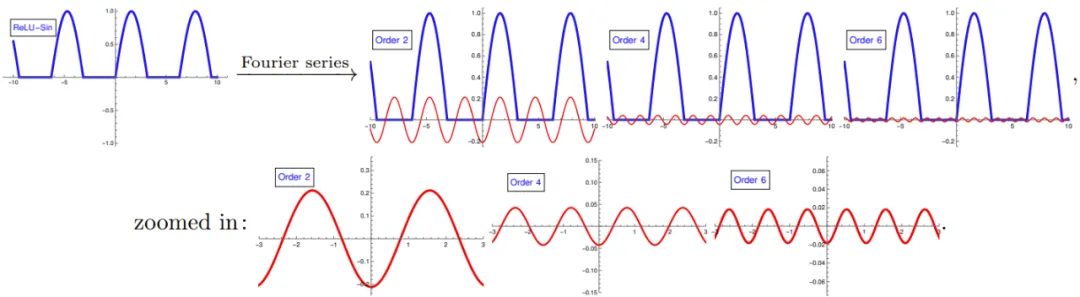
(這里展示了當 ?? 是 ReLU 時,??(sin (x)) 的前幾個傅里葉級數項。)這與我們撥動吉他琴弦時發生的情況非常相似:一個音符具有與所彈奏音符相對應的基頻,以及更高的頻率(泛音,類似于上面底部的三張圖片),它們結合在一起形成了吉他獨特的音色。
該團隊的研究表明:一般情況下,在等變神經網絡中,信息會從更低共振頻率流向更高共振頻率,但反之則不然:
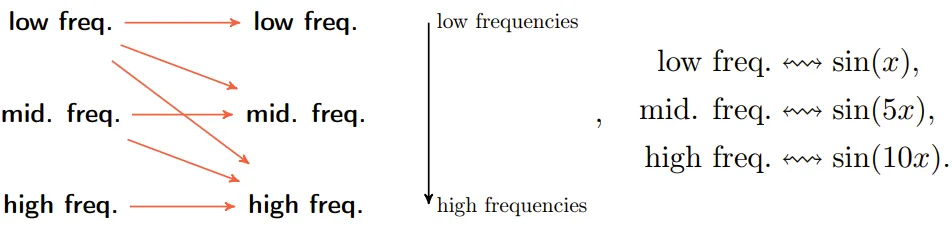
這對等變神經網絡有兩個具體影響:
- 等變神經網絡的大部分復雜性都出現在高頻區,
- 如果想學習一個低頻函數,那么可以忽略神經網絡中與高頻相對應的大部分。
舉個例子,如果使用典型的流式示意圖(稱為交互圖 /interaction graph)表示,一個基于(8 階循環群)構建的等變神經網絡是這樣的:
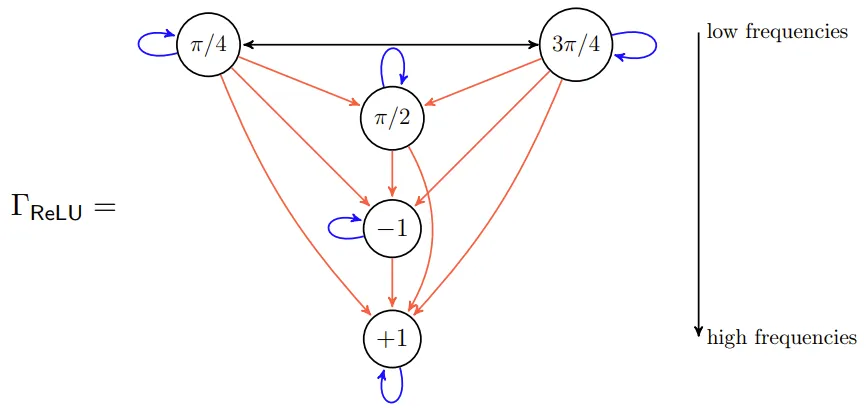
其中的節點是 C_8 的簡單表示,節點中的值表示生成器的動作。在此圖中,「低頻」簡單表示位于頂部,信息從低頻流向高頻。這意味著在大型網絡中,高頻將占據主導地位。
主要貢獻
該團隊做出了一些重要的理論貢獻,主要包括:
- 他們指出將等變神經網絡分解成簡單表示是有意義且有用的。
- 他們論證表明等變神經網絡必須通過置換表示構建。
- 他們證明分段線性(但并非線性)的等變映射的存在受控于類似于伽羅瓦理論的正規子群。
- 他們計算了一些示例,展示了理論的豐富性,即使在循環群等「簡單」示例中也是如此。
等變神經網絡和分段線性表示
該團隊在論文中首先簡要介紹了表示論和神經網絡的基礎知識,這里受限于篇幅,我們略過不表,詳見原論文。我們僅重點介紹有關等變神經網絡和分段線性表示的研究成果。
等變神經網絡:一個示例
這篇論文的出發點是:學習關于某種對稱性的等變映射是有用的。舉些例子:
- 圖像識別結果通常不會隨平移變化,比如識別圖像中的「冰淇淋」時與冰淇淋所在的位置無關;
- 文本轉語音時,「冰淇淋」這個詞不管在文本中的什么位置,都應該生成一樣的音頻;
- 工程學和應用數學領域的許多問題都需要分析點云。這里,人們感興趣的通常是對點云集合的質量評估,而與順序無關。換句話說,這樣的問題不會隨點的排列順序變化而變化。因此,這里的學習問題在對稱群下是不變的。
為了解釋構建等變神經網絡的方式,該團隊使用了一個基于卷積神經網絡的簡單示例,其要處理一張帶周期性的圖像。
這里,這張周期性圖像可表示成一個 n × n 的網格,其中每個點都是一個實數。如果設定 n=10,再將這些實數表示成灰度值,則可得到如下所示的圖像:
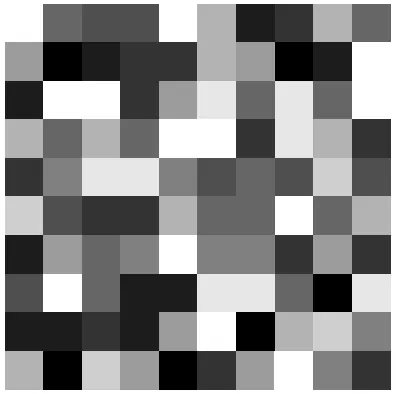
我們可以在這張圖上下左右進行重復,使之具有周期性,也就相當于這張圖在一個環面上。令 C_n = ?/n? 為 n 階循環群,C^2_n = C_n × C_n。用數學術語來說,一張周期性圖像是從群 C^2_n 到 ? 的映射的 ? 向量空間的一個元素: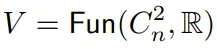 。在這個周期性圖像的模型中,V 是一個「C^2_n 表示」。事實上,給定 (a, b) ∈ C^2_n 和 ?? ∈ V,可通過移動坐標得到一張新的周期性圖像:
。在這個周期性圖像的模型中,V 是一個「C^2_n 表示」。事實上,給定 (a, b) ∈ C^2_n 和 ?? ∈ V,可通過移動坐標得到一張新的周期性圖像:
- ((a, b)?f)(x, y) = f (x + a, y + b)
也就是說,平移周期性圖像會得到新的周期性圖像,例如:

得到等變神經網絡的一個關鍵觀察是:從 V 到 V 的所有線性映射的 ? 向量空間的維度為 n^4,而所有 C^2_n 表示線性映射的 ? 向量空間的維度為 n^2。
下面來看一個 C^2_n 等變映射。對于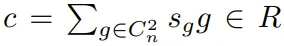 ,可通過一個卷積型公式得到 C^2_n 等變映射 V → V:
,可通過一個卷積型公式得到 C^2_n 等變映射 V → V: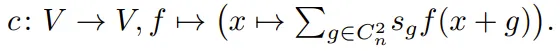
舉個例子,如果令 c = 1/4 ((1, 0) + (0, 1) + (?1, 0) + (0, ?1))。則 c??? 是周期性圖像且其像素 (a, b) 處的值是其相鄰像素 (a+1, b)、(a, b+1)、(a?1, b) 和 (a, b?1) 的值的平均值。用圖像表示即為:
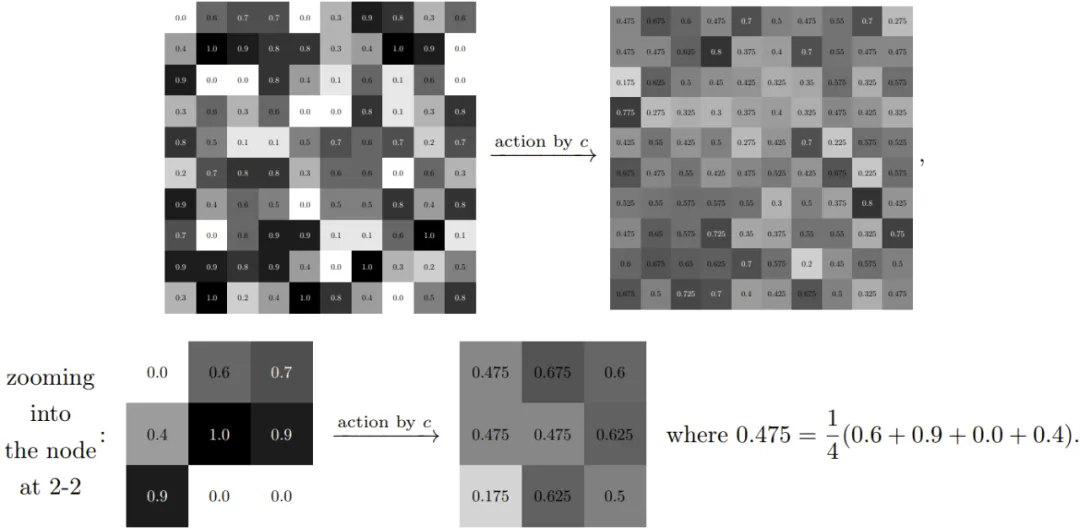
更一般地,不同 c 的卷積可對應圖像處理中廣泛使用的各種映射。
現在,就可以定義這種情況下的 C^2_n 等變神經網絡了。其結構如下:
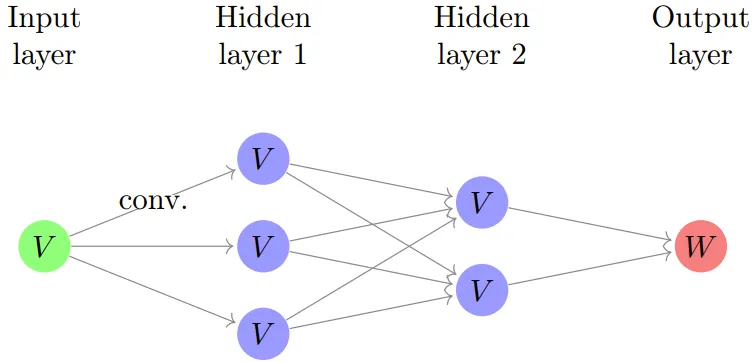
其中每個箭頭都是一個卷積。此外,W 通常是 ? 或 V。上圖是一張卷積神經網絡的(經過簡化的)圖像,而該網絡在機器學習領域具有重要地位。對于該網絡的構建方式,值得注意的主要概念是:
- 此神經網絡的結構會迫使得到的映射 V → W 為等變映射。
- 所有權重的空間比傳統的(全連接)神經網絡小得多。在實踐中,這意味著等變神經網絡所能處理的樣本比「原始」神經網絡所能處理的大得多。(這一現象也被機器學習研究者稱為權重共享。)
該團隊還指出上圖隱式地包含了激活圖,而他們最喜歡的選擇是 ReLU。這意味著神經網絡的組成成分實際上是分段線性映射。因此,為了將上述的第二個主要觀察(通過將問題分解成簡單表示來簡化問題)用于等變神經網絡,很自然就需要研究分段線性表示論。
等變神經網絡
下面將給出等變神經網絡的定義。該定義基于前述示例。
令 G 為一個有限群。Fun (X, ?) 是有限群 G 的置換表示(permutation representation)。
定義:等變神經網絡是一種神經網絡,其每一層都是置換表示的直接和,且所有線性映射都是 G 等變映射。如圖所示:
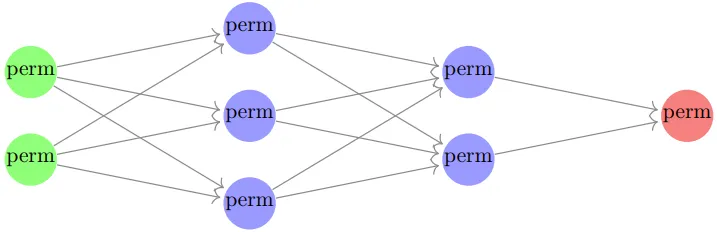
(這里,綠色、藍色和紅色點分別表示輸入、隱藏層和輸出層,perm 表示一個置換表示,它們并不一定相等。和普通的原始神經網絡一樣,這里也假設始終會有一個固定的激活函數,其會在每個隱藏層中被逐個應用到分量上。)
最后舉個例子,這是一個基于點云的等變神經網絡,而點云是指 ?^d 中 n 個不可區分的點構成的集合。這里 n 和 d 為自然數。在這種情況下,有限群 G 便為 S_n,即在 n 個字母上的對稱群,并且其輸入層由 (?^d)^n = (?^n)^d 給定,而我們可以將其看作是 d 個置換模塊 Fun ({1, ..., n}, ?) 的副本。如果將 Fun ({1, ..., n}, ?) 寫成 n,則可將典型的等變神經網絡表示成:
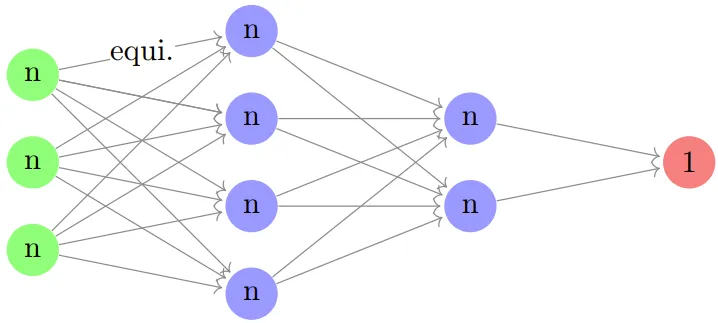
(這里 d=3 且有 2 層隱藏層。)這里的線性映射應當是 S_n 等變映射,而我們可以基于下述引理很快確定出可能的映射。
引理:對于有限 G 集合 X 和 Y,有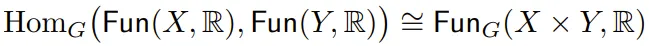 ,其中 Fun_G (X × Y, ?) 表示 G 不變函數 X×Y →?。
,其中 Fun_G (X × Y, ?) 表示 G 不變函數 X×Y →?。
根據該引理,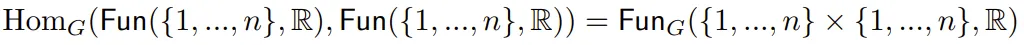 ,并且 G = S_n 有兩條由對角及其補集(complement)給出的軌道。因此,存在一個二維的等變映射空間 n→n,并且這與 n 無關。(在機器學習領域,這種形式的 S_n 的等變神經網絡也被稱為深度網絡。)
,并且 G = S_n 有兩條由對角及其補集(complement)給出的軌道。因此,存在一個二維的等變映射空間 n→n,并且這與 n 無關。(在機器學習領域,這種形式的 S_n 的等變神經網絡也被稱為深度網絡。)
為了更詳細地理解等變神經網絡以及相關的分段線性表示論的定義、證明和分析,請參閱原論文。










































