繼AlphaFold 3掀起生物學革命后，DeepMind又要開始發力量子力學了。

8月22日，他們最新的研究成果FermiNet登上了Science，使用神經網絡對量子激發態進行準確計算。

論文地址：https://www.science.org/doi/abs/10.1126/science.adn0137

而是將問題轉化為尋找擴展系統的基態問題。論文介紹了一種通過變分蒙特卡羅（variational Monte Carlo）估計量子系統激發態的算法，而是將問題轉化為尋找擴展系統基態的問題，因此非常適用于神經網絡分析。

通過在兩種不同的神經網絡：FermiNet和Psiformer上運行，作者驗證了這種方法的準確性。

其中FerminNet同樣由DeepMind和帝國理工學院于2020年聯名提出，論文發表在期刊《Physical Review Research》上。

論文地址：https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.2.033429

這篇論文展示了深度學習如何幫助求解量子力學基本方程，提出的創新網絡架構FermiNet非常適合對大量電子集合（即化學鍵的基本構建塊）的量子態進行建模。

更重要的是，FermiNet首次展示了，如何用深度學習方法、根據第一性原理計算原子和分子的能量，其準確度足以發揮實際作用。

這不僅是一個重要的基礎科學問題，而且還可能在未來產生實際用途，比如在制造新材料和化學合成物之前，使用計算機進行模擬或原型制作。

此外，FermiNet在蛋白質折疊、玻璃動力學、晶格量子色動力學等領域都可能有廣泛的用途。

FeimiNet相關代碼已經公布在GitHub上，方便計算物理和計算化學領域相關研究的參考。

倉庫地址：https://github.com/google-deepmind/ferminet

除了FermiNet，DeepMind在2022年發布的基于自注意力的架構Psiformer仍然是迄今為止用于求解量子力學方程的最準確的AI方法。

論文地址：https://arxiv.org/abs/2211.13672

量子力學簡史

沒有什么比「量子力學」這四個字更能讓人困惑的了，畢竟這是讓普朗克都為之頭禿的領域。

比如薛定諤思維實驗里那只又死又活的貓，還有經典物理完全無法描述的——粒子和波的性質同時存在。

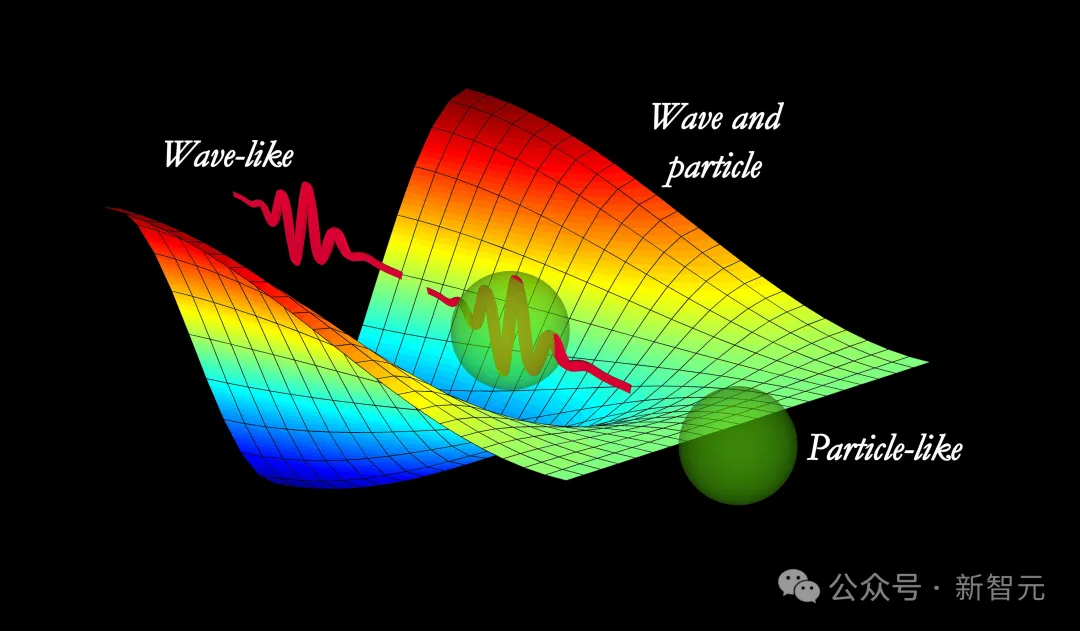
https://www.livescience.com/24509-light-wave-particle-duality-experiment.html

在經典模型中，原子核位于中間，固定數量的電子繞著固定的軌道運行，如同太陽系一般嚴謹有序。

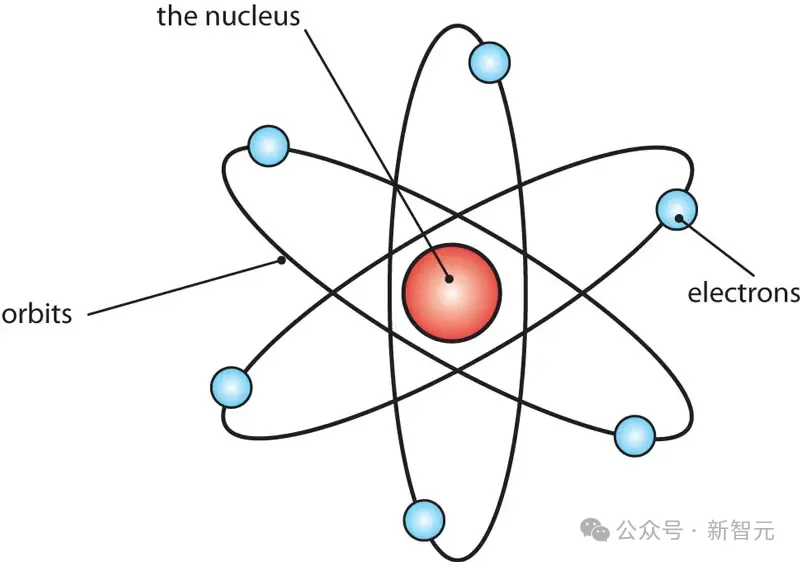
但在量子系統中，電子等粒子完全沒有這種精確的軌道，它們的位置是由「概率云」描述的。

「概率云」是什么意思？

這個模型告訴我們，原子中的電子沒有固定的運動軌跡，也沒有確切的位置，只能用「電子概率密度」描述它們在某個區域出現的概率。

然而，概率云模型給我們的僅僅是「概率」而已，無法真正判斷電子在任何特定時刻是否位于某個區域。

https://www.sciencefacts.net/electron-cloud.html

這種情況已經超出了一般人類能理解的范疇，因此著名物理學家Richard Feynman才會宣稱：「如果你認為自己理解量子力學，那你就根本不理解量子力學。」

雖然直覺無法理解，語言解釋起來也很困難，但是理論的核心內容可以用非常簡潔的數學語言描述。

所以計算機科學領域常聽到的「Talk is cheap, show me your code」，在理論物理也有類似的一句話——「Shut up and calculate」。

在核心的幾個方程中，最著名的是薛定諤方程，足以描述所有熟悉物質在原子和原子核水平上的行為。

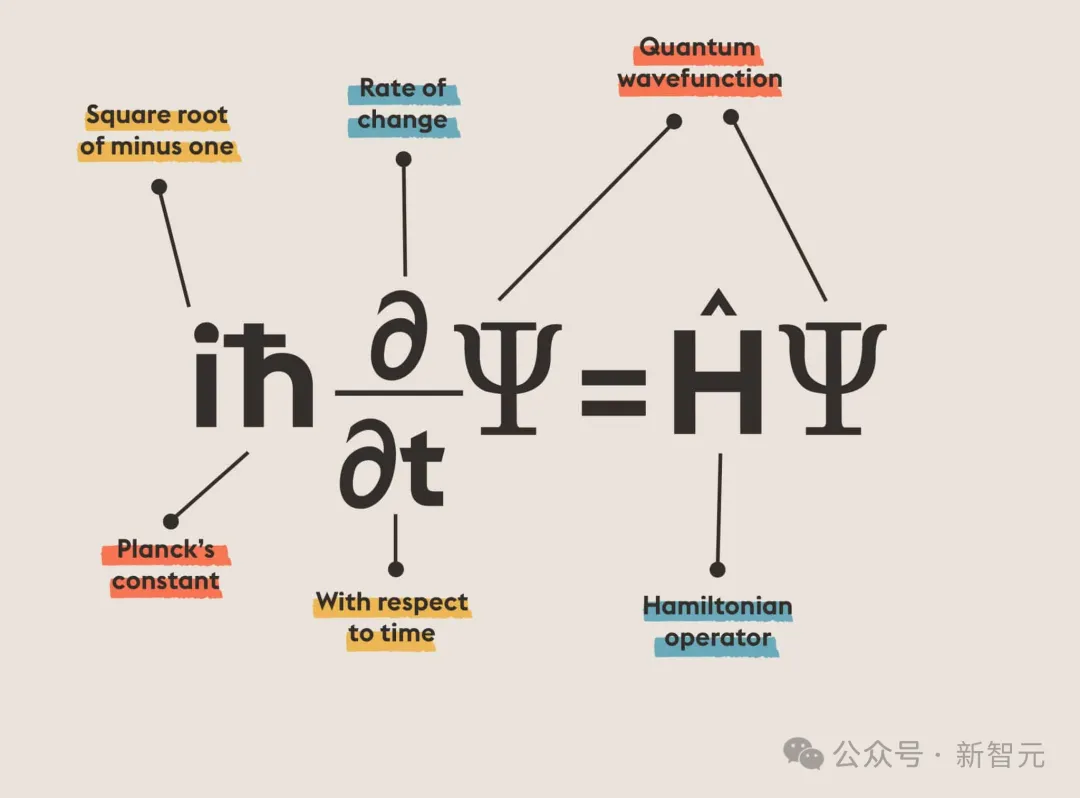
https://abakcus.com/directory/schrodingers-equation/

化學中的共價鍵，或者超導體、超流體、激光和半導體的各種反直覺性質，都是電子間量子相互作用的結果，也都可以用薛定諤方程來描述。

上世紀20年代，量子力學的相關規則出現后，科學家們第一次可以用詳細理論描述化學反應的最底層原理。

比如，對不同分子建立相應方程，求解系統的能量，就可以找出哪些分子處于穩定態，哪些分子間會自發地發生反應。

然而，理想很美好，現實很骨感。

當科學家們實際開始計算時，他們發現，只有氫原子的方程可以求解——其他的都太復雜了，算不出來。

因此，量子力學奠基人之一、物理學家Paul Dirac在1929年說了這樣一句話，到今天依舊適用——

「要描述大部分物理學和整個化學的數學理論，所必需的基本物理定律是完全已知的。困難只在于，要精確應用這些定律的話，會導致方程過于復雜而無法求解。」

「所以，我們需要開發能應用量子力學的近似方法。」

Dirac之后，物理學家使用了一種近似方法，將電子分配到一個特定的軌道，每個軌道的形狀由所有其他軌道平均得到。

這種「平均場」方法只給每個電子分配一個軌道，因此對電子實際行為的描述非常不完整，但依然是一個可行的方法，對分子總能量的估算誤差在0.5%左右

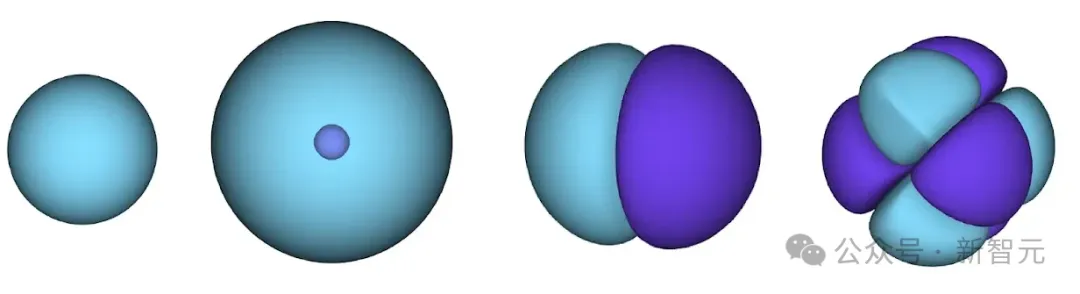
原子軌道示意圖，藍色或紫色區域的表面表示最有可能找到電子的區域；藍色區域波函數為正，紫色區域波函數為負

然而，誤差為0.5%的方法依舊不夠。

要知道，分子鍵能量僅僅占系統總能量中的微小部分，想正確預測分子是否處于穩定態，要依靠占比0.001%的能量差值來判斷，或剩余相關能量中的0.02%。

相比電子平均場，近幾十年開發的多種計算方法都取得了進步，但總是不能在同時達到令人滿意的準確率和計算效率。

為費米子量身定做神經網絡

表示量子系統的挑戰之處在于，必需為每種可能的電子位置分配相應概率，這就構成了一個極其龐大的構型空間。

比如，單單是硅原子，其可能的電子構型數量就會比宇宙中所有原子的數量加起來還要多。而這正是深度神經網絡的用武之地。

過去幾年中，神經網絡在表示復雜的高維概率分布方面取得了巨大的進步，而且能以有效、可擴展的方式進行訓練。它們在AI領域中擬合高維函數的能力，或許也能用于表示量子的波函數。

泡利不相容原理

處理電子時，還需要考慮一個問題——電子必須遵守泡利不相容原理（Pauli exclusion principle），這意味著它們不能同時處于同一空間。

因為電子屬于「費米子」，其波函數必須是反對稱（antisymmetric）的。如果交換兩個電子的位置，波函數就會乘以-1。這意味著如果兩個電子彼此重疊，則波函數（以及該構型的概率）將為零。

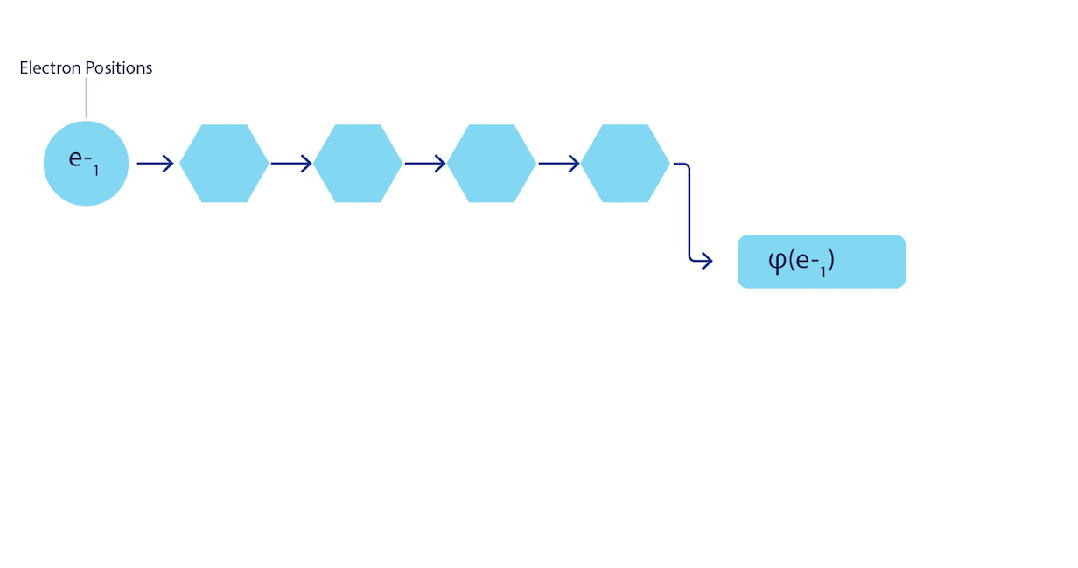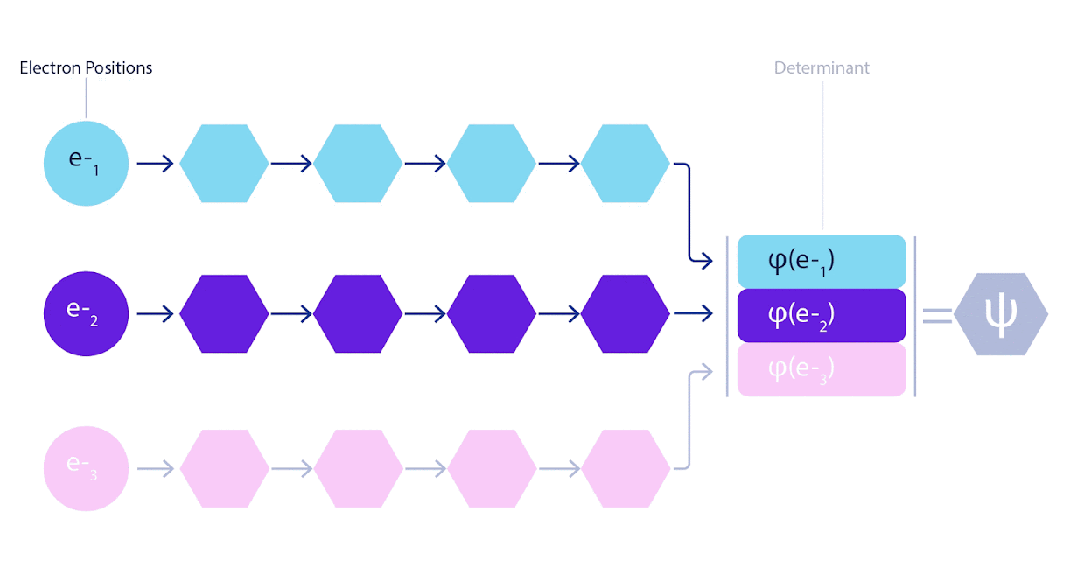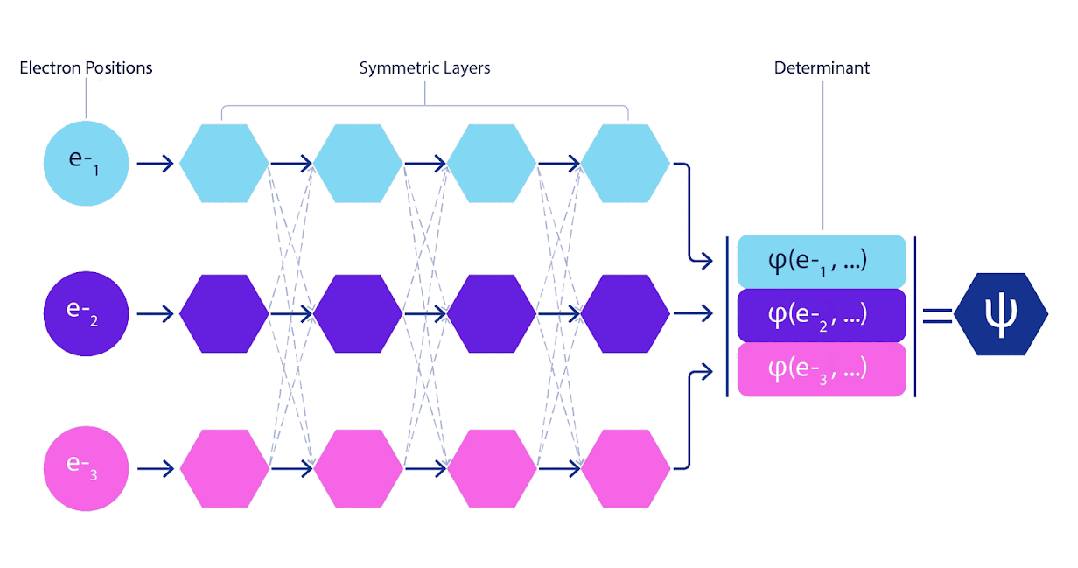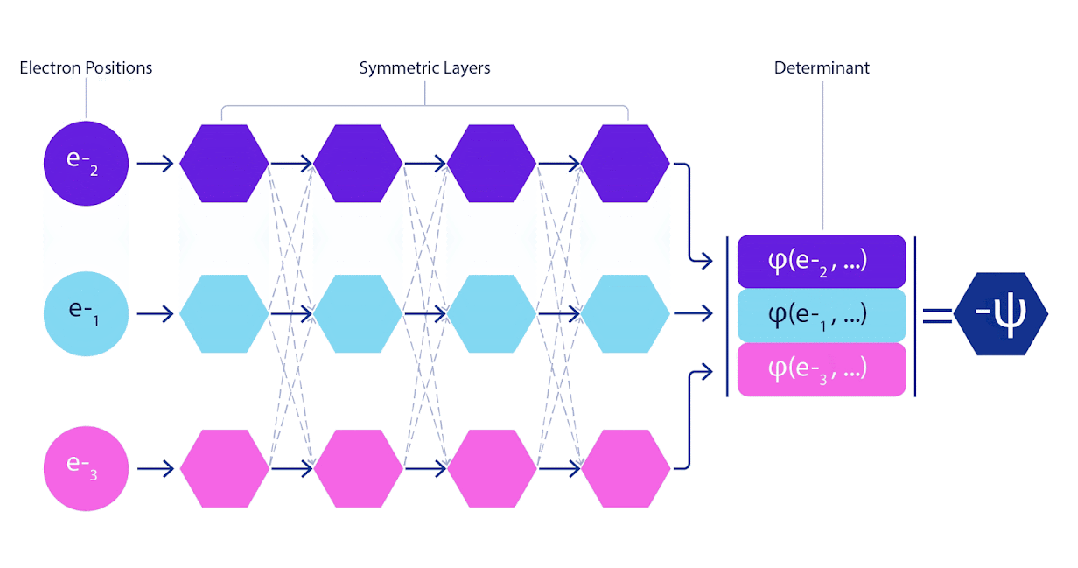
這意味著我們需要開發一種新的神經網絡，接受反對稱結構的輸入——這就是FermiNet。

矩陣的行列式恰好具有這種「反對稱」屬性：如果交換兩行，輸出就會乘以-1，就像費米子的波函數一樣。因此在大多數量子化學方法中，「反對稱性」是通過行列式引入的。

Slater行列式就采用了這種思路：使用單電子函數對系統中的每個電子進行評估，并將所有結果打包到一個矩陣中，該矩陣的行列式就是反對稱波函數。

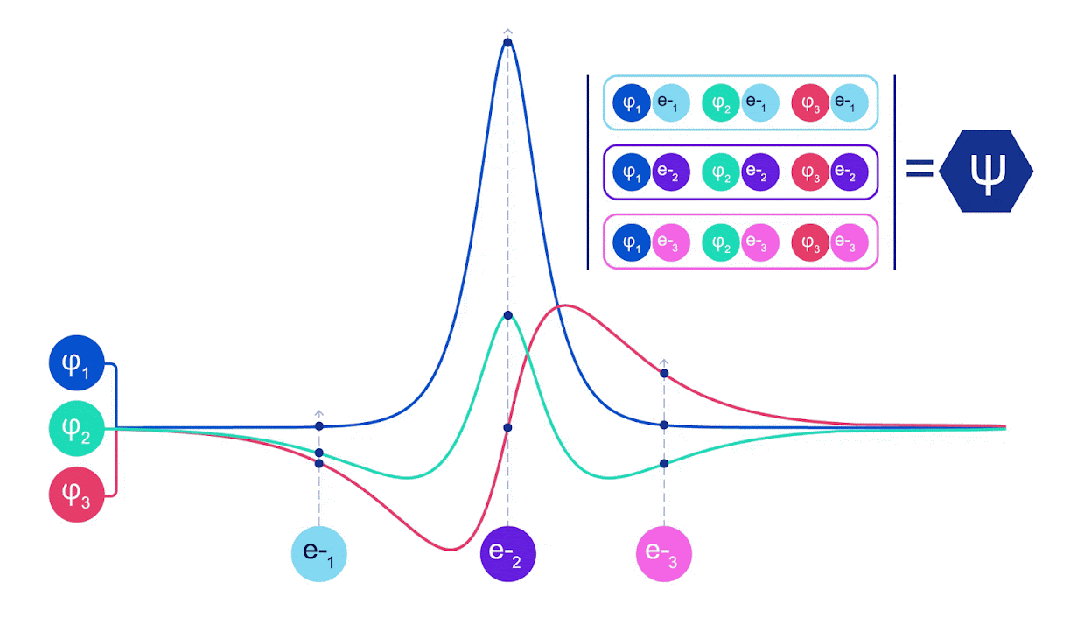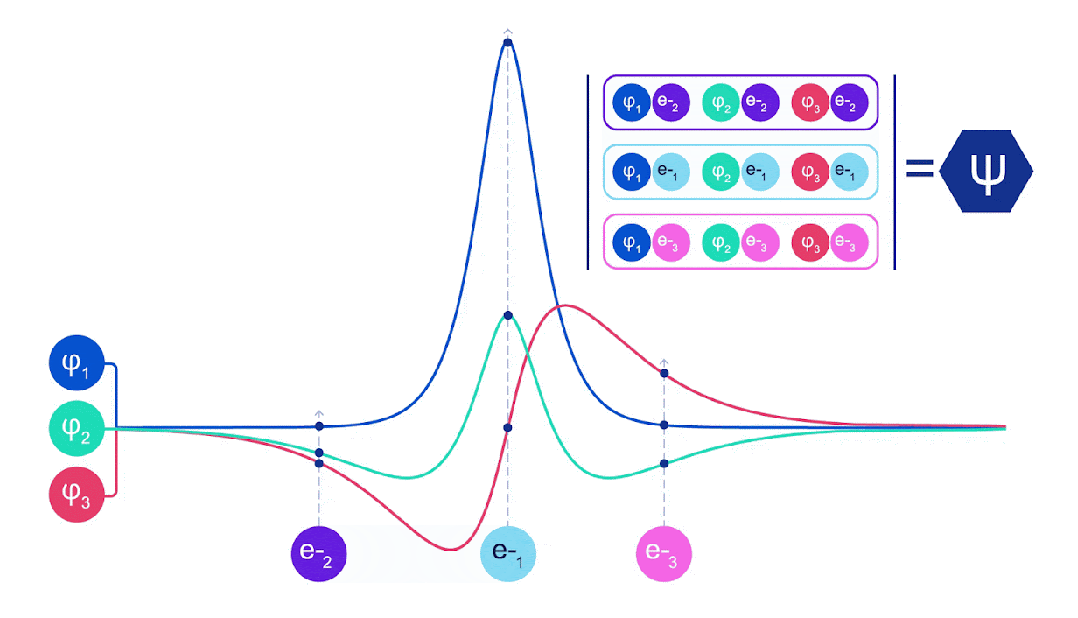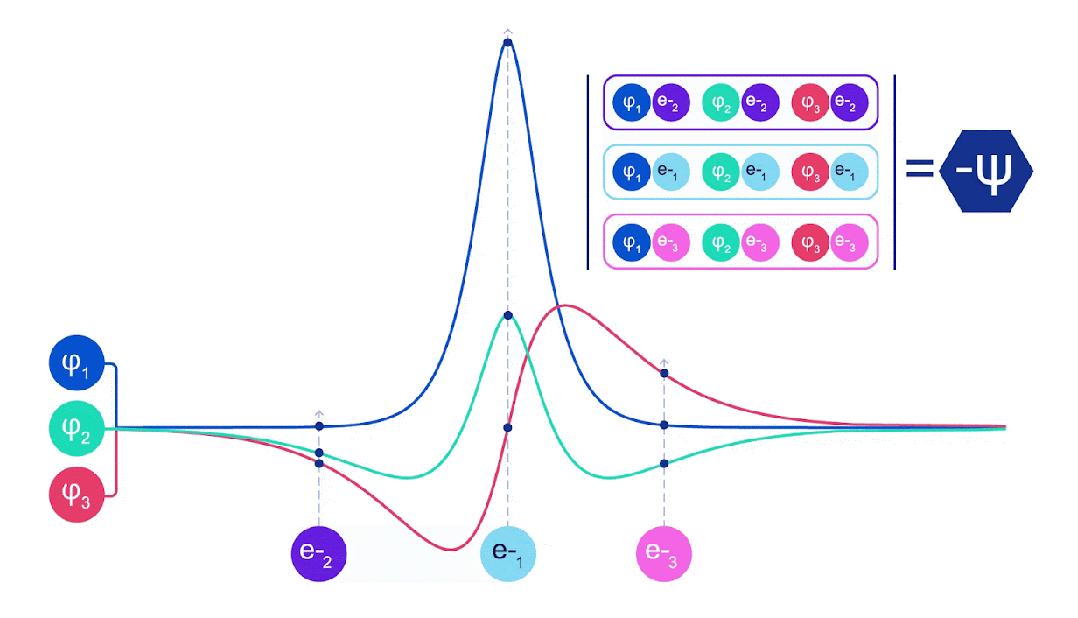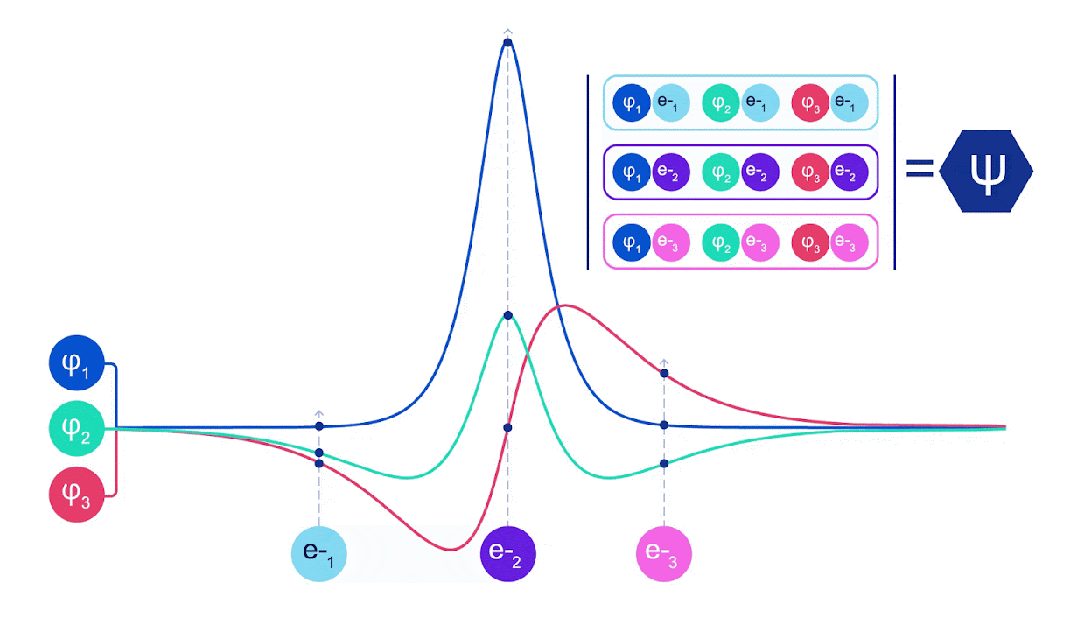
Slater行列式的動畫演示：每條曲線都是上面所示軌道之一的切片當，電子1和2交換位置時，對應于Slater行列式發生行交換，波函數乘以-1，保證遵循泡利不相容原理

在表示復雜函數方面，深度神經網絡通常比基函數的線性組合更有效。

在FermiNet中，進入行列式的每個函數都是所有電子的函數，這遠遠超出了僅使用單個電子或兩個電子構建函數的方法（如Slater行列式）。

此外，FermiNet中每個電子都對應單獨的信息流。但如果這些流之間沒有任何交互，FermiNet的表達能力也不會比Slater行列式有所提升。

因此，網絡中每一層所有流的信息都被平均后，才會傳遞到下一層的信息流中，這類似于圖神經網絡在每一層聚合信息的方式。

因此，與Slater行列式不同，如果神經網絡層變得足夠寬，FermiNet就可以作為通用函數逼近器。這意味著，如果得到正確訓練，FermiNet就能夠擬合薛定諤方程的近似精確解。

FermiNet的動畫演示：網絡的單個流（藍色、紫色或粉色）的功能與傳統軌道非常相似。FermiNet引入了流之間的對稱交互，使波函數更加通用、表達能力更強，且保留了Slater行列式的反對稱特性

變分量子蒙特卡羅

如果要準確地通過最小化系統能量來擬合FermiNet，就需要評估所有可能出現的電子構型的波函數。顯然，我們不能直接計算其精確值，只能估算其近似值。

我們隨機選擇電子配置，評估每種電子排布的局部能量，將其相加后進行最小化。

與直接計算真實的能量最小值不同，這種估算方法被稱為蒙特卡羅方法（Monte Carlo method），有點像賭徒一遍又一遍地擲骰子。雖然得到的只是近似值，但如果需要使其更精確，我們隨時可以再次擲骰子。

這些電子排布的樣本從何而來呢？

由于波函數的平方給出了在任何位置觀察到某種特定粒子排布的概率，因此從波函數本身生成樣本是最方便的——本質上是模擬觀察粒子的行為。

雖然大多數神經網絡根據外部數據進行訓練，但在FermiNet中，用于訓練的輸入數據由神經網絡本身生成的。這意味著，除了指定原子核的結構和位置，我們不需要任何額外的訓練數據。

這種思想被稱為「變分量子蒙特卡羅」（variational quantum Monte Carlo, VMC）。雖然60年代就被提出，但通常被認為是一種低成本且不精確的計算方法。

通過用FermiNet替換Slater行列式，VMC成功「改頭換面」，準確率得到了極大的提升。

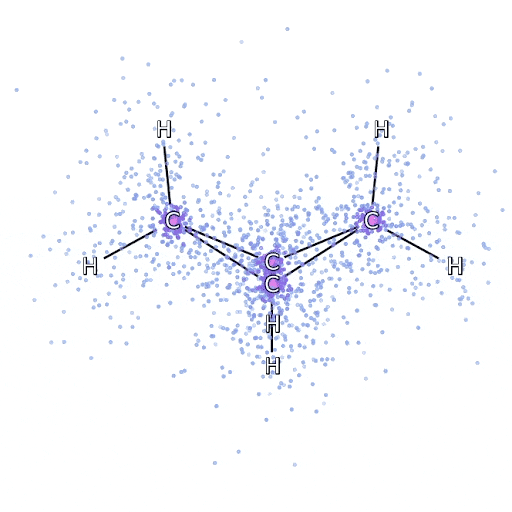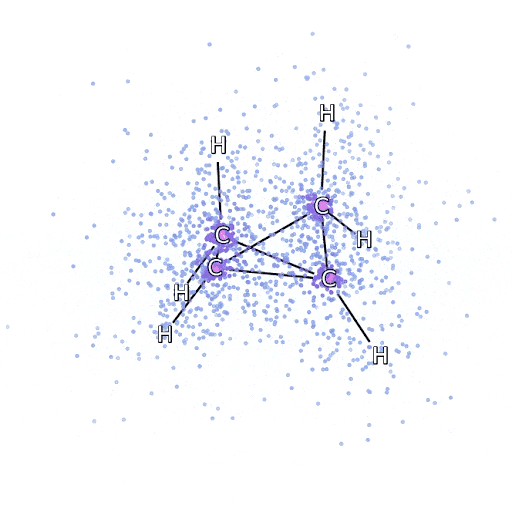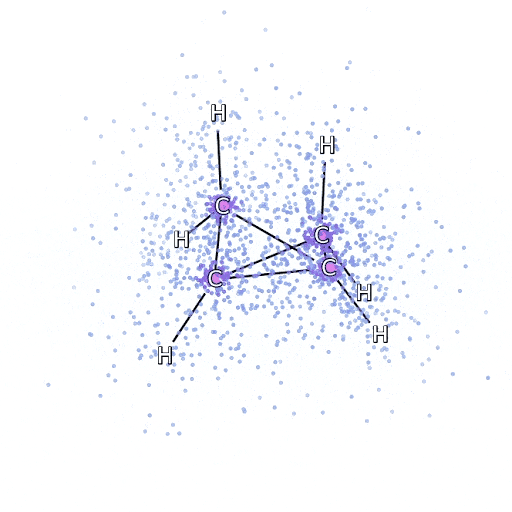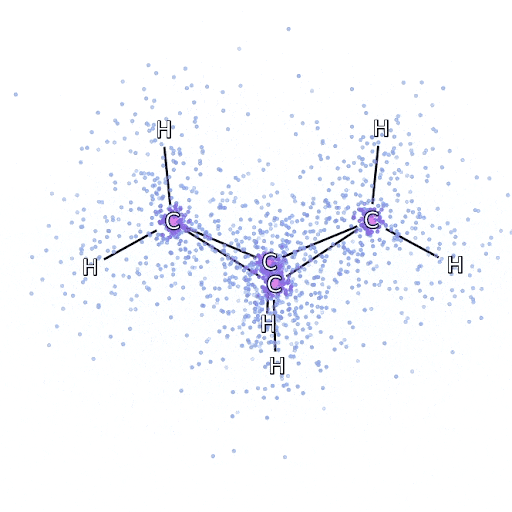
從FermiNet采樣：模擬電子圍繞雙環丁烷分子移動

實驗結果

我們首先從簡單的、經過充分研究的系統開始：元素周期表第一行中的原子（氫到氖）。

這些都是小型系統，電子數≤10個，而且足夠簡單——甚至簡單到可以用最準確且最昂貴（指數擴展）的方法來處理它們。

結果發現，FermiNet的性能遠遠優于類似的VMC方法——相對于計算量以指數級別增長的方法，誤差通常能降低一半或更多。

在較大的系統上，指數擴展的方法過于復雜，因此使用耦合聚類方法（coupled cluster method）作為基線。

耦合聚類方法對于穩定構型的分子效果很好，但很難應對化學鍵拉伸或斷裂時的情況，而后者對于理解化學反應恰恰至關重要。

另外，雖然這種方法的計算效率比指數擴展的方法要好得多，但實驗所用方法的計算量仍以電子數量的七次方的速度增加，因此也只能用于中等大小的分子。

下一階段，將FermiNet應用于逐漸變大的分子，從氫化鋰到雙環丁烷。

對于最小的分子，FermiNet捕獲了耦合簇能量和單個Slater行列式獲得的能量之間的99.8%的差異。

雙環丁烷是我們研究過的最大的系統，有 30 個電子，FermiNet仍然捕獲了97%或更多的相關能量（correlation energy），考慮到我們應用的方法非常簡單，這是一個巨大的成就。

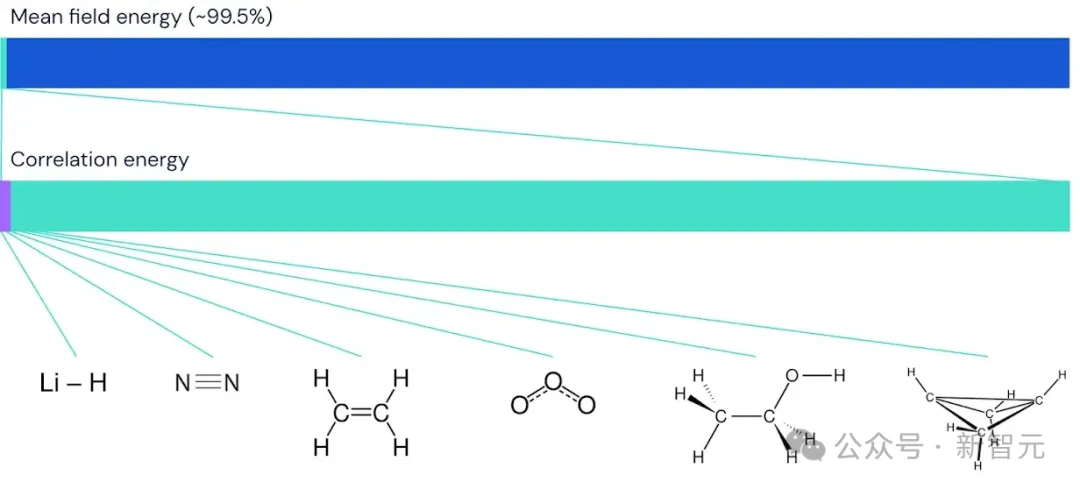
FermiNet在分子上捕獲的相關能量比例：紫色表示99%的相關能量，從左到右：氫化鋰、氮氣、乙烯、臭氧、乙醇和雙環丁烷。

計算激發態的新方法

除了2020年提出的FermiNet，在Science上最新發表的成果中，DeepMind為計算量子化學領域中最困難挑戰之一提出了解決方案——了解分子如何在激發態之間轉變。

FermiNet最初專注于分子的基態，即給定一組原子核，找到其周圍電子的最低能量排布。

但是，當分子和材料受到大量能量的激發時，例如光照或高溫，電子可能會進入更高的能量狀態——激發態。

激發態是理解物質與光相互作用的基礎，不同的分子和材料會吸收/釋放確切數量的能量，這相當于它們獨特的指紋。

對這方面原理的理解影響著太陽能電池板、LED、半導體、光催化劑等技術的性能，也在涉及光的生物過程中發揮著關鍵作用，例如光合作用和視覺。

準確計算激發態能量比計算基態能量更具挑戰性。即使是基態化學的黃金基準方法，如上面提到的耦合簇，在計算激發態能量時也會有大數十倍的誤差。

雖然我們希望將FermiNet的工作擴展到激發態，但目前來看，神經網絡還不能與與最先進的方法競爭。

因此，這篇論文提出了一種計算激發態的新方法，比以前的方法更強大、更通用，可以應用于任何類型的數學模型，包括FermiNet和其他神經網絡。

其工作原理是找到具有額外粒子的擴展系統的基態，因此對現有的優化算法進行少量修改即可使用。

論文在廣泛的基準上進行了驗證，并取得了非常理想的實驗結果。carbon dimer

在雙原子碳（carbon dimer）這種小而復雜的分子上，該方法實現了4meV的平均絕對誤差 (MAE)，而之前的gold standard方法，誤差為20meV，相當于五倍更接近實驗結果。

雙原子碳示意圖

此外，作者還在計算化學中一些最具挑戰性的系統上進行了測試，比如兩個電子同時被激發。結果發現。與迄今為止完成的最苛刻、最復雜的計算相比，誤差僅在0.1 eV。