陶哲軒最新力作，在“自然數(shù)倒數(shù)之和是否為有理數(shù)”問題上取得一系列進(jìn)展。

其中最引人矚目的一項成果，就是證明了一個非常反直覺的猜想，居、然、是、對、的：

存在一個遞增的自然數(shù)級數(shù)ak，使得對任意有理數(shù)t，都是有理數(shù)。（）

一位Topos研究所的數(shù)學(xué)物理學(xué)家John Carlos Baez在評論區(qū)毫不掩飾自己的驚嘆：

哇哦，這個結(jié)論太反直覺了！
不過這也意味著這項研究非常有趣。

為啥說這個結(jié)論非常反直覺？

可以理解成，要使一個級數(shù)的和是有理數(shù)本來就很難，再加上任意有理數(shù)t的偏移量，還讓級數(shù)保持有理性，難度就又加幾個數(shù)量級了。

• 需要滿足對所有有理數(shù)t都成立，而有理數(shù)有無窮多個
• 每增加一個t，就相當(dāng)于增加一個約束條件
• 改變序列中任何一個數(shù)字a_k，都會同時影響所有t對應(yīng)的級數(shù)和

數(shù)學(xué)家Kenneth Stolarsky或許也是如上所想的，所以提出了相反的Stolarsky猜想。

現(xiàn)在，陶哲軒的結(jié)論相當(dāng)于證明了Stolarsky猜想是不成立的。

果然，數(shù)學(xué)的神奇之處就在于，有時看似不可能的事情實際上是可能的，只是解決方案可能超出了我們的直觀認(rèn)知。

那么，陶哲軒的方法是怎么顛覆直覺的？

迭代逼近法解決無限維度問題

從論文提交歷史可以看到，這項研究原本只有Vjekoslav Kova?一個作者，研究的是兩個特定級數(shù)的有理性問題。

陶哲軒加入后，幫助Kova?擴(kuò)展到了對整個Ahmes級數(shù)的研究。

原本只有6頁的短論文，也擴(kuò)展成了28頁長篇論證……

除了論文之外，陶哲軒還在個人博客上解釋了他們的思路。

不是直接嘗試構(gòu)造這個級數(shù)，而是把問題轉(zhuǎn)化為研究一種集合，再使用“迭代逼近”方法，逐步解決。

先來解釋一下什么是Ahmes級數(shù)。

Ahmes級數(shù)是滿足如下形式的無窮級數(shù)，其中a_k是一個嚴(yán)格遞增的自然數(shù)序列。

由于大多數(shù)實數(shù)都是無理數(shù)，人們也會期望這樣的級數(shù)“通常”也是無理的，但很難確定一個特定級數(shù)的無理性。

首先，此前數(shù)學(xué)界已知道，如果a?的增長速度比C^(2k)更快（對任意常數(shù)C），那么對應(yīng)的Ahmes級數(shù)一定是無理數(shù)。

也就是存在一個明確的“增長速度分界線”，超過這個速度，級數(shù)必然無理。但接近這個速度時，仍可能找到有理的例子。

接下來，論文中表明了如果滿足a???=O(a?2)，意味著a???比a?2增長得慢得多。

那么可以找到一個可比較的級數(shù)b?，和a?是漸進(jìn)關(guān)系，且∑(1/b?)是有理數(shù)。

這部分解決了Erd?s問題#263：序列a? =2^2k是否符合這個性質(zhì)，是否所有增長速度不超過指數(shù)級的級數(shù)都有這個性質(zhì)。

因為條件a???=O(a?2)不足以覆蓋a? =2^2k的情況，這個條件也不適用于所有指數(shù)級或更慢增長的序列。

也就是a???=O(a?2)作為問題的分界線，“差一點”就能完整的解決了。

在這之后，陶哲軒展示了一個新的變體結(jié)論：

如果級數(shù)a?滿足：a???=O(a?)（即下一項不會比當(dāng)前項增長太快） 且∑(1/a?)收斂。

那么可以找到b?，使得：b?=a?+O(1)（即b?與a?只差一個有界的常數(shù)） 且∑(1/b?)是有理數(shù)。

這又和Erd?s問題#264相關(guān)：

其中a?=2^k時的情況被完全解決了，因為2^k是指數(shù)增長。

問題中的第二部分，關(guān)于a?=k!的情況，超出了當(dāng)前方法的能力范圍。

新的分界線被定位到了指數(shù)增長。

就像這樣……一步一步迭代逼近，就到了Erd?s問題#266，也是更高維度的變體。

陶哲軒避免了任何數(shù)論難題，主要依賴有理數(shù)集的可數(shù)稠密性。（具體論證過程略）

最終，Stolarsky猜想被轉(zhuǎn)化為一個無限維的問題。

陶哲軒讓維度數(shù)d隨k增長，但增長的速度要保持夠慢，這樣既保證收斂又保證稠密性。

不是陶解決的第一個Erd?s問題

前面提到，陶哲軒給出結(jié)論的的這個問題，是Erd?s問題#266。

由沃爾夫數(shù)學(xué)獎獲得者、匈牙利數(shù)學(xué)家Paul Erd?s（1913年3月26日－1996年9月20日）提出。

不過，這個問題的相關(guān)起源最早能追溯到古埃及時期——

古代埃及人在進(jìn)行分?jǐn)?shù)運算時，只使用分子是1的分?jǐn)?shù)。因此這種分?jǐn)?shù)也叫做埃及分?jǐn)?shù)，或者叫單分子分?jǐn)?shù)。

他們把所有復(fù)雜分?jǐn)?shù)，都表示成單分子分?jǐn)?shù)的和，例如3/4，一定要表示成3/4=1/2+1/4。

故而很長一段時間（大概幾千年吧），數(shù)學(xué)史家都堅持認(rèn)為古埃及人不會使用分?jǐn)?shù)；現(xiàn)代數(shù)學(xué)家們也一度認(rèn)為埃及人之所以未能把算術(shù)和代數(shù)發(fā)展到較高水平，其分?jǐn)?shù)運算之繁雜（就是非要把真分?jǐn)?shù)分解成單分子分?jǐn)?shù)）也是原因之一。

等到數(shù)學(xué)家們發(fā)現(xiàn)里面隱含了何等豐富的內(nèi)容，已經(jīng)是兩千多年后的后話了。

OK，讓我們回到Erd?s問題和Erd?s本人。

Erd?s被譽(yù)為20世紀(jì)最富有創(chuàng)造力的數(shù)學(xué)家和數(shù)學(xué)猜想提出者之一，21歲時就被授予數(shù)學(xué)博士學(xué)位，論文導(dǎo)師也是馮·諾伊曼的恩師利波特·費杰爾（Léopold Féjér）。

Erd?s一輩子合作了超過500位數(shù)學(xué)家，畢生發(fā)表了約1525篇數(shù)學(xué)論文，數(shù)量之多，至今無人能及。

他窮其一生，致力于并提出了離散數(shù)學(xué)、圖論、數(shù)論、數(shù)學(xué)分析、逼近理論、集合論和概率理論中的問題，其中大部分工作集中在離散數(shù)學(xué)領(lǐng)域，解決了該領(lǐng)域許多以前未解決的難題。

83歲時，因心臟病突發(fā)，Erd?s去世在華沙的一個數(shù)學(xué)會議上。

如他所愿，他的墓志銘上寫道：我終于不再變笨了（Végre nem butulok tovább）。

值得一提的是，Erd?s問題#266不是陶哲軒解決的第一個Erd?s相關(guān)問題。

2015年9月，陶哲軒在arXiv上掛了一篇論文《The Erd?s discrepancy problem》，宣布證明了Paul Erd?s在20世紀(jì)30年代提出的數(shù)論猜想“埃爾德什差異問題”存在。

埃爾德什差異問題于1932年被Erd?s提出，此前困擾了學(xué)術(shù)界80多年。

與許多數(shù)論難題一樣，埃爾德什差異問題描述起來很簡單，但證明難度卻很大。

通俗點闡述它：

假如你有一個由1和-1（例如由扔硬幣隨機(jī)產(chǎn)生）組成的數(shù)列和常數(shù)C。你要尋找到一個足夠長的有限數(shù)列，使這一數(shù)列的總和大于常數(shù)C。

有意思的是，為了證實這個曾經(jīng)的猜想，陶哲軒經(jīng)過了多年手動計算和計算機(jī)嘗試，還加入過一個專門研究它的小分隊合力專研（雖然當(dāng)時失敗了）。

最終，破題的靈感來自德國數(shù)學(xué)家尤威·斯特羅斯基在陶博客下的評論，暗示陶研究的另一個問題可能與埃爾德什差異問題有關(guān)。

“起初，我認(rèn)為這種聯(lián)系只是表面的。”但陶哲軒很快意識到將新思路和已有的結(jié)果結(jié)合在一起，很可能得到問題的證明。

這件事在當(dāng)年當(dāng)月，登上了Nature，題為《數(shù)學(xué)天才解決了一個大師級謎題》。

更有意思的是，Erd?s和陶哲軒的緣分，能追溯到更更更早。

1985年，72歲的Erd?s去澳大利亞講學(xué)。

在阿德萊德大學(xué)（8歲起，中學(xué)生陶哲軒用1/3的時間在該校學(xué)習(xí)數(shù)學(xué)、物理課程）的安排下，時年10歲的小陶哲軒拜見了Erd?s。

Erd?s認(rèn)真閱讀了陶哲軒寫的論文，并鼓勵他說：“你是很棒的孩子，繼續(xù)努力！”

后來，Erd?s還寫了推薦信，推薦陶哲軒到普林斯頓大學(xué)攻讀博士學(xué)位。

2010年，英國衛(wèi)報評選了兩千多年來“世界十大數(shù)學(xué)天才”，認(rèn)為他們的革命性發(fā)現(xiàn)改變著我們的世界——Erd?s和陶哲軒都榜上有名。

這兩位數(shù)學(xué)大家還有一張非常經(jīng)典的合影：

2013年，Erd?s誕辰100周年之際，陶哲軒在自己的博客上分享了一張當(dāng)年和Erd?s的珍貴合影，以表懷念和感激。

One More Thing

But！

雖然#266被陶給出了結(jié)論，但Paul Erd?s還留下了很多問題沒被解決，這些問題通常是他在與其他數(shù)學(xué)家的合作中提出的，也有些是他獨自思考后形成的。

這些問題涵蓋了數(shù)論、組合數(shù)學(xué)、圖論、概率論等多個數(shù)學(xué)領(lǐng)域。

目前，860個問題中，還有580個問題等著被探索（去掉#266也還有579個）。這些問題分別設(shè)置了0-10000美元的獎金。

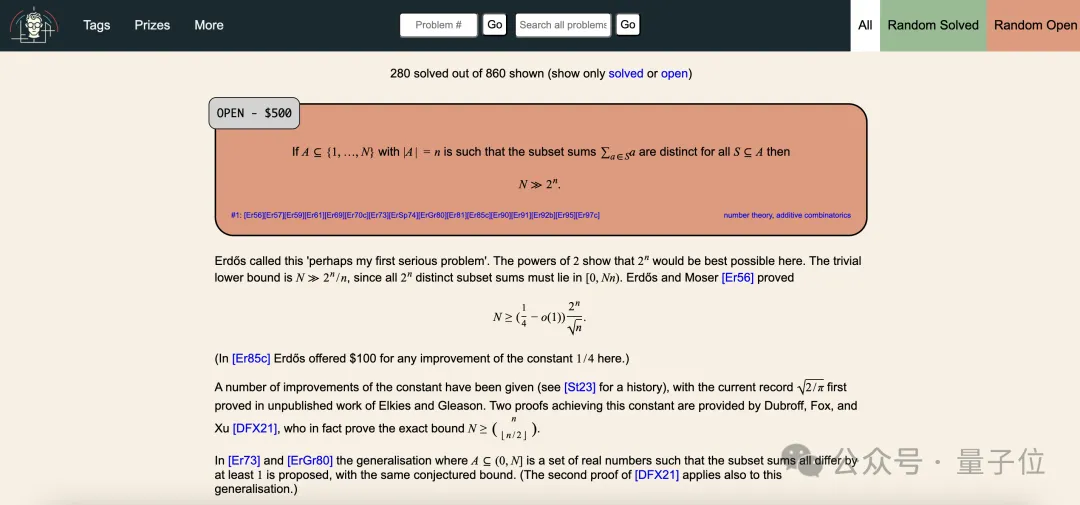
這些燦爛又迷人的遺產(chǎn)，直到今天仍激勵著每一位數(shù)學(xué)家，推動數(shù)學(xué)的進(jìn)步，也讓后來者從中獲得新的視角和靈感。

論文地址：https://arxiv.org/abs/2406.17593v3