時間序列預測的不確定性區間估計:基于EnbPI的方法與應用研究
在現代預測分析領域,準確評估預測結果的不確定性已成為一個關鍵挑戰。預測的不確定性量化不僅能夠提供更可靠的決策支持,還能深入揭示模型的預測能力邊界。本文聚焦于時間序列預測中的不確定性量化問題,重點探討基于一致性預測理論的集成批量預測區間(Ensemble Batch Prediction Interval, EnbPI)方法。
傳統一致性預測方法的核心假設——數據可交換性(exchangeability)——在時間序列分析中面臨重大挑戰。時間序列數據本質上包含了重要的時序依賴特征,如趨勢、周期性和季節性模式,這使得觀測值的順序信息對預測至關重要。因此,在構建時間序列預測的不確定性量化框架時,必須保持數據的時序完整性。
EnbPI的工作原理
2021年提出的EnbPI方法為解決這一技術難題提供了創新解決方案。該方法突破了傳統一致性預測對數據可交換性的依賴,能夠有效處理非平穩時間序列數據和復雜的時空依賴關系。
EnbPI的核心思想是在數據的不同子集上訓練基礎模型,并通過集成這些模型來構建預測區間。EnbPI通過自舉采樣(Bootstrap Sampling)方法創建數據子集,即對時間序列進行有放回隨機采樣。
作為時間序列領域的一致性預測擴展,EnbPI具有以下技術優勢:
- 構建分布無關的預測區間,實現近似邊際覆蓋率
- 支持任意估計器的集成
- 推理階段計算效率高,無需模型重訓練
- 適用于小規模數據集,不需要額外的校準集
需要注意的是,由于需要訓練多個模型,EnbPI的訓練階段會消耗較多計算資源。
EnbPI的核心技術框架
EnbPI方法的核心思想是通過集成學習范式構建預測區間。該方法通過自舉采樣技術在時間序列數據上構建多個子集,并在這些子集上訓練獨立的預測模型。這種方法具有以下技術優勢:
1.方法論優勢
- 構建分布無關的預測區間
- 實現近似邊際覆蓋率
- 保持時序數據的結構特征
2.實踐優勢
- 支持任意基礎預測器的集成
- 推理階段計算效率高
- 無需額外的模型重訓練
- 適用于小規模數據集分析
3.技術局限
- 訓練階段計算開銷較大
- 需要針對具體應用場景優化集成規模
這種系統性的方法論框架為時間序列預測的不確定性量化提供了堅實的理論基礎,同時也為實踐應用提供了可操作的技術路徑。
EnbPI算法實現流程
EnbPI算法可分為訓練和預測兩個主要階段,每個階段包含兩個關鍵步驟。在開始訓練EnbPI集成之前,需要首先選擇合適的基礎估計器。該估計器可以是任何機器學習模型,包括梯度提升樹、神經網絡、線性回歸或傳統統計模型。
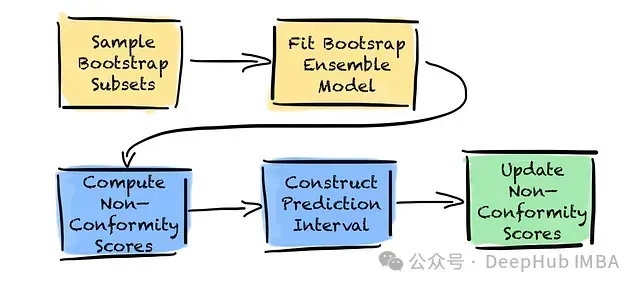
EnbPI算法流程圖。黃色框表示訓練階段的步驟,藍色框表示預測階段的步驟,綠色框表示可選的在線更新步驟。
1.訓練階段詳解
訓練階段主要包含兩個核心步驟:從訓練數據中生成非重疊子集,并在每個子集上訓練模型。
第1步:自舉子集采樣
在生成子集之前,首先需要確定集成模型的規模。每個集成成員都需要一個獨立的自舉樣本。
子集采樣的關鍵要求是保持非重疊性。這意味著每個子集都是獨特的,且與其他子集相互獨立。每個子集包含原始數據集中的不同數據片段。通過在不同數據子集上訓練模型,能夠引入模型間的變異性,從而增強集成的多樣性并降低過擬合風險。
集成規模的選擇需要根據數據集大小進行權衡。數據集較小時,可生成的非重疊子集數量有限,因為每個子集都需要足夠的數據量來保證模型訓練的有效性。較小的集成規模會導致多樣性不足,從而影響EnbPI方法的性能,具體表現為預測區間偏寬。
增加模型數量通常能提升性能表現,產生更窄的預測區間。這是因為更大規模的集成能夠捕獲數據中更豐富的變異性,同時通過聚合更多預測來提高模型穩健性。這也意味著更高的計算成本。
實踐表明,20到50個模型的集成規模通常能夠在計算效率和預測準確性之間取得良好的平衡。
確定集成規模后,需要為每個集成成員創建相應的數據子集。子集通過從原始數據集中有放回抽樣獲得。
值得注意的是,為了保持時間序列數據的時序依賴性,采樣單位為數據塊而非單個觀測值。由于采用有放回采樣,某些數據塊可能在子集中重復出現,而其他塊可能未被選中。
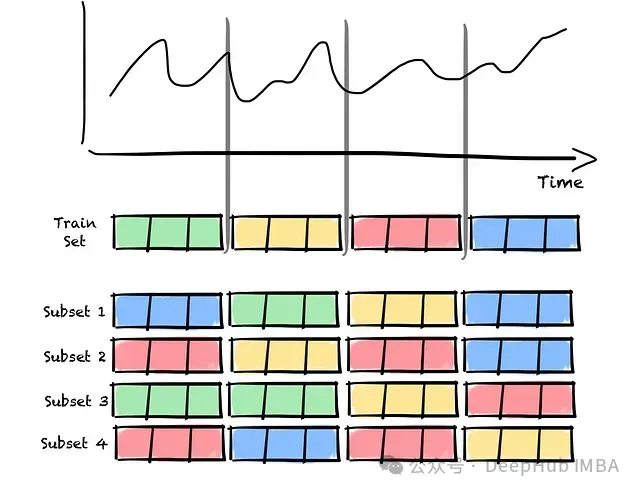
時間序列自舉采樣流程示意圖。原始時間序列被分割為多個數據塊,每個子集通過隨機有放回采樣這些數據塊構建而成,數據塊可能在子集內重復出現。
完成自舉采樣后,即可進入模型訓練階段。
第2步:訓練自舉集成模型
對每個自舉子集訓練一個獨立的模型,從而構建一個具有多樣性的模型集成。由于各個模型在不同數據子集上訓練,即使面對相同的輸入數據也會產生不同的預測結果。這種預測的多樣性是獲得穩健預測區間估計的關鍵因素。
2.預測階段實現機制
第3步:留一法(LOO)估計實現
在完成集成模型訓練后,需要評估集成模型在未知數據上的預測方差,用于校準集成并確定預測區間的寬度。在EnbPI框架中,非一致性分數定義為真實值與預測值之間的偏差。這里需要解決的關鍵問題是校準數據集的選擇。
由于集成中的每個估計器都在訓練集的不同子集上進行訓練,沒有任何單個估計器接觸過完整的訓練數據。這一特性使得我們可以直接利用訓練集進行校準,無需額外的校準數據集。
對訓練集中的每個觀測值,采用集成進行預測,但僅使用訓練過程中未接觸過該觀測值的估計器。隨后通過聚合函數(如均值或中位數)對這些模型的預測結果進行匯總。
聚合函數的選擇會影響預測的穩健性。均值聚合雖然對異常值較為敏感,但能夠有效降低整體誤差;中位數聚合則具有較強的異常值抵抗能力,適用于噪聲較大的數據場景。因此聚合函數的選擇需要根據具體的數據特征和應用需求進行確定。
通過聚合預測可以計算每個觀測值的非一致性分數。這種方法實質上利用了樣本外誤差作為非一致性度量,為后續未知數據的預測校準提供基礎。
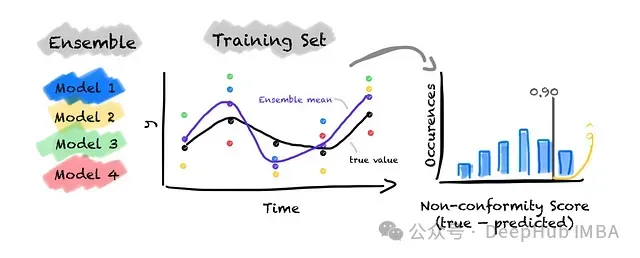
EnbPI集成示例(包含4個基礎模型)的校準過程圖解。對于訓練集中的每個觀測值,僅使用訓練過程中未見過該觀測值的模型進行預測。例如,對第一個觀測值僅使用模型3和4進行預測(因為該觀測值出現在模型1和2的訓練子集中)。預測結果通過均值聚合(紫色點)。對第二個觀測值可使用模型1、3和4,因為僅模型2的訓練集包含該觀測值。依此類推完成所有訓練集觀測值的預測。通過計算集成均值與真實值之間的誤差得到非一致性分數。最后根據分數分布和預設的顯著性水平α確定截斷值q。
第4步:預測區間構建方法
對于未知數據的預測,使用所有訓練完成的集成估計器進行預測,并采用與第3步相同的聚合函數對單個預測結果進行匯總,得到的值作為預測區間的中心點。
預測區間的構建基于第3步獲得的殘差分布。通過預先設定的顯著性水平確定截斷值,將該值在預測中心點的基礎上進行加減運算,從而得到預測區間的上下界。
第5步:非一致性分數的動態更新機制(可選)
上述方法使用的非一致性分數僅基于訓練數據計算,在接收到新數據后并不進行更新。這導致預測區間的寬度保持不變,無法反映數據分布或模型性能的動態變化。此限制在基礎數據特征或模型表現發生顯著變化時可能帶來問題。
為解決這一問題,可以在獲取新觀測值時動態更新非一致性分數。這一過程無需重新訓練集成估計器,僅需重新計算非一致性分數。通過這種機制,預測區間能夠及時反映最新的數據特征和模型動態,實現區間寬度的自適應調整。
3.EnbPI方法的實驗驗證
為了驗證EnbPI方法的有效性,我們這里選擇了德國電力價格預測這一實際應用場景。在實驗數據中,我們特意在最后兩周的數據中引入了100歐元/兆瓦時的人工偏移,用于評估預測區間對突發性變化的適應能力。
通過初步數據分析,我們觀察到電力價格數據具有明顯的雙重周期性特征:
- 日內周期:由于用電負載的日內分布規律,價格在早晚高峰時段顯著上升
- 周度周期:工作日的電力價格普遍高于周末,這反映了工商業用電需求的周期性變化
基于對數據特征的理解,我們構建了以下特征集:
- 時間特征:包括日、月、年等基礎時間維度,以及工作日/周末標識
- 歷史數據特征:包含過去7天的同時段歷史價格,以及基于過去24小時的滑動平均價格(滯后一天)
以下是特征工程的具體實現:
# %% 特征工程實現
forecast_horizon = 24 # 預測時間窗口設置為24小時
# 時間特征提取
price_data["year"] = price_data["dt"].dt.year
price_data["month"] = price_data["dt"].dt.month
price_data["day"] = price_data["dt"].dt.day
# 周末標識特征構建
price_data["is_weekend"] = (price_data["dt"].dt.dayofweek >= 5).astype(int)
# 歷史同期價格特征構建
for day in range(forecast_horizon, 7 * forecast_horizon, forecast_horizon):
price_data[f"hour_lag_{day}"] = price_data["y"].shift(day)
# 24小時滑動平均價格特征
price_data["ma_24"] = (
price_data["y"].rolling(window=24, center=False, closed="left").mean().shift(24)
)
price_data.set_index("dt", inplace=True)為了全面評估模型性能,我們采用了較長的測試周期。雖然實際應用中通常只需要預測未來24小時的價格,但我們選擇使用最后30天的數據作為測試集,這使我們能夠更好地觀察和評估預測區間的動態變化特性。
# %% 數據集劃分
test_horizon = forecast_horizon * 30 # 測試集長度設為30天
X_train = price_data.iloc[:-test_horizon].drop(columns=["y"])
y_train = price_data["y"].iloc[:-test_horizon]
X_test = price_data.iloc[-test_horizon:].drop(columns=["y"])
y_test = price_data["y"].iloc[-test_horizon:]
_, ax = plt.subplots(1, figsize=(10, 3))
ax.plot(y_train, label="train")
ax.plot(y_test, label="test")
ax.set_ylabel("price in EUR/MWh")
ax.legend()
ax.grid()為了便于結果可視化和性能評估,我們實現了一個專門的結果分析函數:
# %% 結果分析與可視化函數
def plot_results(y_test, y_pred, y_pred_int):
fig, ax = plt.subplots(figsize=(10, 3))
ax.plot(y_test, label="Actual")
ax.plot(y_test.index, y_pred, label="Predicted", ls="--")
ax.fill_between(
y_test.index, y_pred_int[:, 0, 0], y_pred_int[:, 1, 0], color="green", alpha=0.2
)
ax.set_ylabel("price in EUR/MWh")
ax.legend(loc="best")
ax.grid()
fig.tight_layout()
# 計算覆蓋率和區間寬度指標
coverage = regression_coverage_score(y_test, y_pred_int[:, 0, 0], y_pred_int[:, 1, 0])
width_interval = regression_mean_width_score(y_pred_int[:, 0, 0], y_pred_int[:, 1, 0])
print(f"Coverage: {coverage:}")
print(f"Width of the interval: {width_interval}")基礎模型選擇與集成實現
為了簡單起見,我們選擇LightGBM作為基礎預測模型。需要說明的是,雖然本文重點不在于優化基礎模型性能,但在實際應用中,基礎模型的預測準確性直接影響預測區間的質量。
EnbPI集成模型的構建與訓練
EnbPI的實現采用了模塊化的方式。首先,使用Mapie的BlockBootsrap類生成自舉樣本。我們設置了20個不重疊的數據塊,每個塊的長度與預測時域(24小時)相匹配。
EnbPI模型的具體實現
以下代碼展示了EnbPI模型的完整實現過程。使用Mapie庫的MapieTimeSeriesRegressor類來封裝模型,并通過參數配置實現預測功能:
# %% EnbPI模型實現
cv_mapie_ts = BlockBootstrap(n_resamplings=20, length=24, overlapping=False, random_state=42)
params = {"objective": "rmse"}
model = lgb.LGBMRegressor(**params)
mapie_enbpi = MapieTimeSeriesRegressor(
model,
method="enbpi",
cv=cv_mapie_ts,
agg_function="mean",
n_jobs=-1,
)
mapie_enbpi = mapie_enbpi.fit(X_train, y_train)
# 設置顯著性水平為0.05,對應95%的置信水平
alpha = 0.05
y_pred, y_pred_int = mapie_enbpi.predict(X_test, alpha=alpha, ensemble=True, optimize_beta=True)
plot_results(y_test, y_pred, y_pred_int)4.實驗結果分析
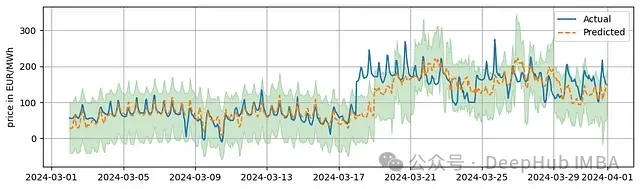
實驗結果顯示,模型達到了91%的覆蓋率,略低于預期的95%目標值,預測區間的平均寬度為142.62歐元/兆瓦時。覆蓋率未達預期的主要原因可能是測試期間出現的價格突變。預測區間寬度在整個測試期間保持相對穩定。
5.非一致性分數的動態更新實現
為了提高模型對數據變化的適應能力,還可以實現了基于partial_fit()方法的動態更新機制。這種實現模擬了實際場景中逐步獲取新數據的情況:
# %% 實現帶動態更新的EnbPI模型
cv_mapie_ts = BlockBootstrap(n_resamplings=20, length=24, overlapping=False, random_state=42)
model = lgb.LGBMRegressor(**params)
mapie_enbpi = MapieTimeSeriesRegressor(
model,
method="enbpi",
cv=cv_mapie_ts,
agg_function="mean",
n_jobs=-1,
)
mapie_enpbi = mapie_enbpi.fit(X_train, y_train)
# 初始化預測結果存儲數組
y_pred_pfit = np.zeros(y_pred.shape)
y_pred_int_pfit = np.zeros(y_pred_int.shape)
# 首次預測
y_pred_pfit[:forecast_horizon], y_pred_int_pfit[:forecast_horizon, :, :] = mapie_enbpi.predict(
X_test.iloc[:forecast_horizon, :], alpha=alpha, ensemble=True, optimize_beta=True
)
# 逐步更新預測
for step in range(forecast_horizon, len(X_test), forecast_horizon):
# 使用新數據更新模型
mapie_enbpi.partial_fit(
X_test.iloc[(step - forecast_horizon) : step, :],
y_test.iloc[(step - forecast_horizon) : step],
)
# 生成下一時段預測
(
y_pred_pfit[step : step + forecast_horizon],
y_pred_int_pfit[step : step + forecast_horizon, :, :],
) = mapie_enbpi.predict(
X_test.iloc[step : (step + forecast_horizon), :],
alpha=alpha,
ensemble=True,
optimize_beta=True,
)
plot_results(y_test, y_pred, y_pred_int)動態更新模型的實驗結果
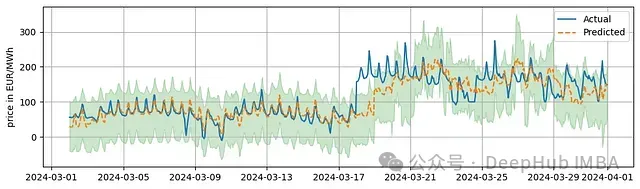
實驗結果表明,即使引入了動態更新機制,模型的整體表現特征與基礎版本相似:覆蓋率維持在91%,預測區間寬度保持在142.62歐元/兆瓦時。這一現象表明,在當前實現中,動態更新機制對預測區間的適應性影響有限。
總結
本研究深入探討了EnbPI方法在時間序列預測不確定性量化中的應用。通過詳細的理論分析和實驗驗證,可以得出以下主要結論:
- EnbPI方法為時間序列預測提供了一個理論完備的不確定性量化框架
- 該方法在實際應用中展現出良好的可操作性和可擴展性
本文的分析和實驗為實踐工作者提供了完整的技術實現參考,有助于將EnbPI方法應用于實際的時間序列預測任務中。


































