Anthropic新研究:用統計思維評估大模型
目前,評估大模型的方法就是比在基準測試中的數值,在于突出SOTA結果,并未充分考慮統計顯著性。例如,在對不同模型進行評估時,若僅依據表面的得分高低判斷優劣,而不考慮數據的不確定性和變異性,可能會得出不準確的結論。
所以,Anthropic提出了將嚴謹的統計思維引入大模型評估領域。通過構建全面的分析框架,能幫助研究人員量化評估結果的精確性,判斷模型之間的差異是否具有統計顯著性,而非僅僅依賴于表面的得分差異,進而為模型的選擇和改進提供更可靠的依據。

我們需要理解評估框架中的一個基本概念——超總體。在統計學中,總體是指研究對象的全體,而超總體則是一個更為宏觀的概念,它包含了所有可能的問題。
在大模型評估的背景下,這意味著不僅僅關注評估中出現的具體問題,而是將這些問題視為從一個更大的、無限的、未觀察到的問題集合中隨機抽取的樣本。這種思維方式允許我們從更宏觀的角度來分析評估數據,從而更準確地估計模型的性能。
在評估框架的理論基礎中,每個問題得分被分解為均值部分和零均值隨機部分。如果一個評估由n個獨立抽取的問題組成,我們可以將第i個問題的得分表示為si,將其分解為均值部分xi和一個零均值隨機部分?i,即si=xi+?i。這里的xi被稱為條件均值,它代表了在給定問題i被選中的情況下的得分均值。
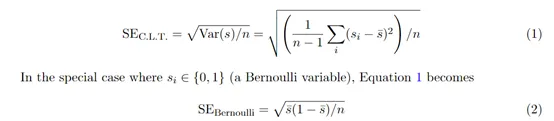
而?i的方差,記作σ2i=Var(?i),被稱為條件方差,它是在問題i被選中的情況下得分的方差。
在這個框架下,可以使用中心極限定理來估計均值的標準誤差。中心極限定理是一個強大的統計學工具,它指出,無論原始數據的分布如何,只要樣本量足夠大,樣本均值的分布將趨近于正態分布。
因此,即使評估得分的分布未知,也可以利用中心極限定理來估計均值的標準誤差,可以估計為SEC.L.T.=√[Var(s)/n]=√[(1/n)Σ(i=1ton-1)(si-ˉs)2]/n,其中ˉs是觀察到的得分的平均值。
但評估中的問題并不總是獨立的。例如,在閱讀理解評估中,多個相關問題可能基于同一文本段落。這種情況下,問題的抽取是非獨立的,中心極限定理的一個關鍵假設被違反,因此直接應用上述公式將導致不一致的標準誤差。
為了解決這個問題,研究人員引入了聚類標準誤差的概念。聚類標準誤差是一種在社會科學中發展出來的技術,用于處理問題聚類中的依賴和相關結構。
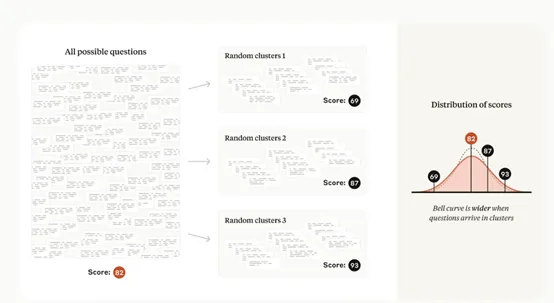
在評估框架的理論基礎中,還有一個重要的概念是方差的降低。方差是衡量得分分布離散程度的統計量,降低方差可以提高估計的精度。方差可以分解為兩個部分:從超總體中選擇問題的方差和所選問題的得分的均值條件方差。這種分解是加性的,遵循全方差定律。
為了展示這種統計學評估方法,研究人員設計了一個假設性的實驗,比較了兩個虛構模型“Galleon”和“Dreadnought”在三個非虛構評估上的表現:MATH(數學推理評估)、HumanEval(Python編程評估)和MGSM(多語言小學數學評估)。
在MATH評估中,Galleon的平均得分為65.5%,標準誤差為0.7%;Dreadnought的平均得分為63.0%,標準誤差為0.7%。
通過計算95%的置信區間,我們可以得出Galleon的真實得分在64.1%到66.9%之間,而Dreadnought的真實得分在62.3%到63.7%之間。這表明Galleon在MATH評估上的表現顯著優于Dreadnought。

在HumanEval評估中,Dreadnought的平均得分為87.7%,標準誤差為2.1%;Galleon的平均得分為83.6%,標準誤差為2.1%。通過計算95%的置信區間,我們可以得出Dreadnought的真實得分在83.6%到91.8%之間,而Galleon的真實得分在79.5%到87.7%之間。這表明Dreadnought在HumanEval評估上的表現顯著優于Galleon。
在MGSM評估中,Dreadnought的平均得分為78.0%,標準誤差為1.7%;Galleon的平均得分為75.3%,標準誤差為1.7%。通過計算95%的置信區間,我們可以得出Dreadnought的真實得分在74.6%到81.4%之間,而Galleon的真實得分在71.9%到78.7%之間。這表明Dreadnought在MGSM評估上的表現也優于Galleon。
通過這些案例分析,我們可以看到,計算標準誤差和置信區間不僅能夠提供更豐富的信息,還能幫助研究者更準確地評估模型在不同任務上的表現。











































