破解聯邦學習中的辛普森悖論,浙大提出反事實學習新框架FedCFA
江中華,浙江大學軟件學院碩士生二年級,導師為張圣宇老師。研究方向為大小模型端云協同計算。張圣宇,浙江大學平臺「百人計劃」研究員。研究方向包括大小模型端云協同計算,多媒體分析與數據挖掘。
隨著機器學習技術的發展,隱私保護和分布式優化的需求日益增長。聯邦學習作為一種分布式機器學習技術,允許多個客戶端在不共享數據的情況下協同訓練模型,從而有效地保護了用戶隱私。然而,每個客戶端的數據可能各不相同,有的數據量大,有的數據量小;有的數據特征豐富,有的數據特征單一。這種數據的異質性和不平衡性(Non-IID)會導致一個問題:本地訓練的客戶模型忽視了全局數據中明顯的更廣泛的模式,聚合的全局模型可能無法準確反映所有客戶端的數據分布,甚至可能出現「辛普森悖論」—— 多端各自數據分布趨勢相近,但與多端全局數據分布趨勢相悖。
為了解決這一問題,來自浙江大學人工智能研究所的研究團隊提出了 FedCFA,一個基于反事實學習的新型聯邦學習框架。
FedCFA 引入了端側反事實學習機制,通過在客戶端本地生成與全局平均數據對齊的反事實樣本,緩解端側數據中存在的偏見,從而有效避免模型學習到錯誤的特征 - 標簽關聯。該研究已被 AAAI 2025 接收。

- 論文標題:FedCFA: Alleviating Simpson’s Paradox in Model Aggregation with Counterfactual Federated Learning
- 論文鏈接:https://arxiv.org/abs/2412.18904
- 項目地址:https://github.com/hua-zi/FedCFA
辛普森悖論
辛普森悖論(Simpson's Paradox)是一種統計現象。簡單來說,當你把數據分成幾個子組時,某些趨勢或關系在每個子組中表現出一致的方向,但在整個數據集中卻出現了相反的趨勢。
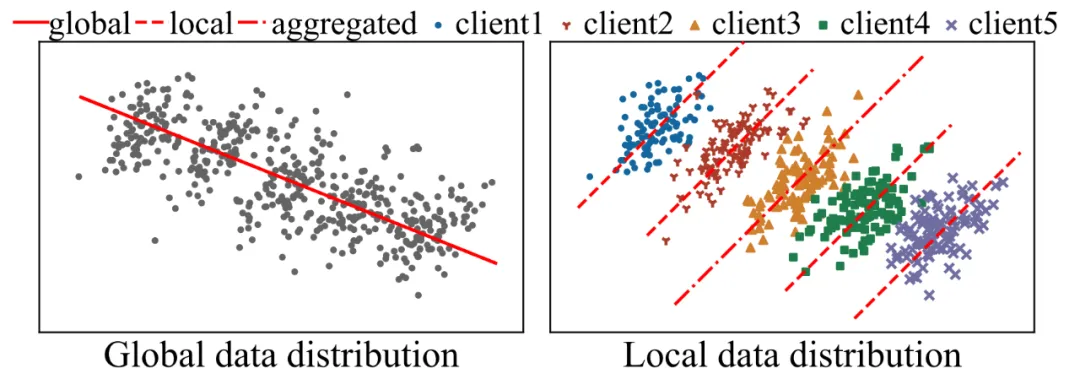
圖 1:辛普森悖論。在全局數據集上觀察到的趨勢在子集上消失 / 逆轉,聚合的全局模型無法準確反映全局數據分布
在聯邦學習中,辛普森悖論可能會導致全局模型無法準確捕捉到數據的真實分布。例如,某些客戶端的數據中存在特定的特征 - 標簽關聯(如顏色與動物種類的關系),而這些關聯可能在全局數據中并不存在。因此,直接將本地模型匯聚成全局模型可能會引入錯誤的學習結果,影響模型的準確性。
如圖 2 所示。考慮一個用于對貓和狗圖像進行分類的聯邦學習系統,涉及具有不同數據集的兩個客戶端。客戶端 i 的數據集主要包括白貓和黑狗的圖像,客戶端 j 的數據集包括淺灰色貓和棕色狗的圖像。對于每個客戶端而言,數據集揭示了類似的趨勢:淺色動物被歸類為「貓」,而深色動物被歸類為「狗」。這導致聚合的全局模型傾向于將顏色與類別標簽相關聯并為顏色特征分配更高的權重。然而,全局數據分布引入了許多不同顏色的貓和狗的圖像(例如黑貓和白狗),與聚合的全局模型相矛盾。在全局數據上訓練的模型可以很容易地發現動物顏色與特定分類無關,從而減少顏色特征的權重。

圖 2:FedCFA 可以生成客戶端本地不存在的反事實樣本,防止模型學習到不正確的特征 - 標簽關聯。
反事實學習
反事實(Counterfactual)就像是「如果事情發生了另一種情況,結果會如何?」 的假設性推理。在機器學習中,反事實學習通過生成與現實數據不同的虛擬樣本,來探索不同條件下的模型行為。這些虛擬樣本可以幫助模型更好地理解數據中的因果關系,避免學習到虛假的關聯。
反事實學習的核心思想是通過對現有數據進行干預,生成新的樣本,這些樣本反映了某種假設條件下的情況。例如,在圖像分類任務中,我們可以改變圖像中的某些特征(如顏色、形狀等),生成與原圖不同的反事實樣本。通過讓模型學習這些反事實樣本,可以提高模型對真實數據分布的理解,避免過擬合局部數據的特點。
反事實學習廣泛應用于推薦系統、醫療診斷、金融風險評估等領域。在聯邦學習中,反事實學習可以幫助緩解辛普森悖論帶來的問題,使全局模型更準確地反映整體數據的真實分布。
FedCFA 框架簡介
為了解決聯邦學習中的辛普森悖論問題,FedCFA 框架通過在客戶端生成與全局平均數據對齊的反事實樣本,使得本地數據分布更接近全局分布,從而有效避免了錯誤的特征 - 標簽關聯。
如圖 2 所示,通過反事實變換生成的反事實樣本使局部模型能夠準確掌握特征 - 標簽關聯,避免局部數據分布與全局數據分布相矛盾,從而緩解模型聚合中的辛普森悖論。從技術上講,FedCFA 的反事實模塊,選擇性地替換關鍵特征,將全局平均數據集成到本地數據中,并構建用于模型學習的反事實正 / 負樣本。具體來說,給定本地數據,FedCFA 識別可有可無 / 不可或缺的特征因子,通過相應地替換這些特征來執行反事實轉換以獲得正 / 負樣本。通過對更接近全局數據分布的反事實樣本進行對比學習,客戶端本地模型可以有效地學習全局數據分布。然而,反事實轉換面臨著從數據中提取獨立可控特征的挑戰。一個特征可以包含多種類型的信息,例如動物圖像的一個像素可以攜帶顏色和形狀信息。為了提高反事實樣本的質量,需要確保提取的特征因子只包含單一信息。因此,FedCFA 引入因子去相關損失,直接懲罰因子之間的相關系數,以實現特征之間的解耦。

全局平均數據集的構建
為了構建全局平均數據集,FedCFA 利用了中心極限定理(Central Limit Theorem, CLT)。根據中心極限定理,若從原數據集中隨機抽取的大小為 n 的子集平均值記為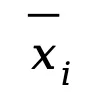 ,則當 n 足夠大時,
,則當 n 足夠大時,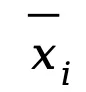 的分布趨于正態分布,其均值為 μ,方差
的分布趨于正態分布,其均值為 μ,方差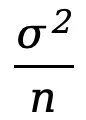 ,即:
,即: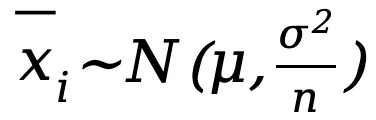 ,其中 μ 和
,其中 μ 和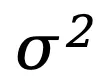 是原始數據集的期望和方差。
是原始數據集的期望和方差。
當 n 較小時, 能更精細地捕捉數據集的局部特征與變化,特別是在保留數據分布尾部和異常值附近的細節方面表現突出。相反,隨著 n 的增大,
能更精細地捕捉數據集的局部特征與變化,特別是在保留數據分布尾部和異常值附近的細節方面表現突出。相反,隨著 n 的增大, 的穩定性顯著提升,其方差明顯減小,從而使其作為總體均值 ?? 的估計更為穩健可靠,對異常值的敏感度大幅降低。此外,在聯邦學習等分布式計算場景中,為了實現通信成本的有效控制,選擇較大的 n 作為樣本量被視為一種優化策略。
的穩定性顯著提升,其方差明顯減小,從而使其作為總體均值 ?? 的估計更為穩健可靠,對異常值的敏感度大幅降低。此外,在聯邦學習等分布式計算場景中,為了實現通信成本的有效控制,選擇較大的 n 作為樣本量被視為一種優化策略。
基于上述分析,FedCFA 按照以下步驟構建一個大小為 B 的全局平均數據集,以此近似全局數據分布:
1.本地平均數據集計算:每個客戶端將其本地數據集隨機劃分為 B 個大小為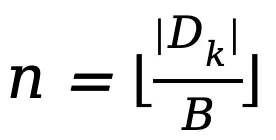 的子集
的子集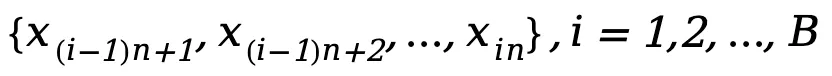 ,其中
,其中 為客戶端數據集大小。對于每個子集,計算其平均值
為客戶端數據集大小。對于每個子集,計算其平均值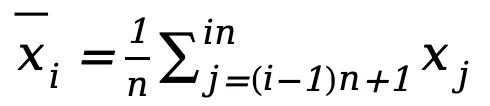 。由此,客戶端能夠生成本地平均數據集
。由此,客戶端能夠生成本地平均數據集 以近似客戶端原始數據的分布。
以近似客戶端原始數據的分布。
2.全局平均數據集計算:服務器端則負責聚合來自多個客戶端的本地平均數據,并采用相同的方法計算出一個大小為 B 的全局平均數據集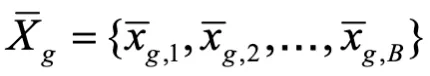 ,該數據集近似了全局數據的分布。對于標簽 Y,FedCFA 采取相同的計算策略,生成其對應的全局平均數據標簽
,該數據集近似了全局數據的分布。對于標簽 Y,FedCFA 采取相同的計算策略,生成其對應的全局平均數據標簽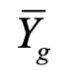 。最終得到完整的全局平均數據集
。最終得到完整的全局平均數據集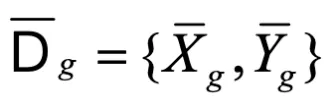
反事實變換模塊
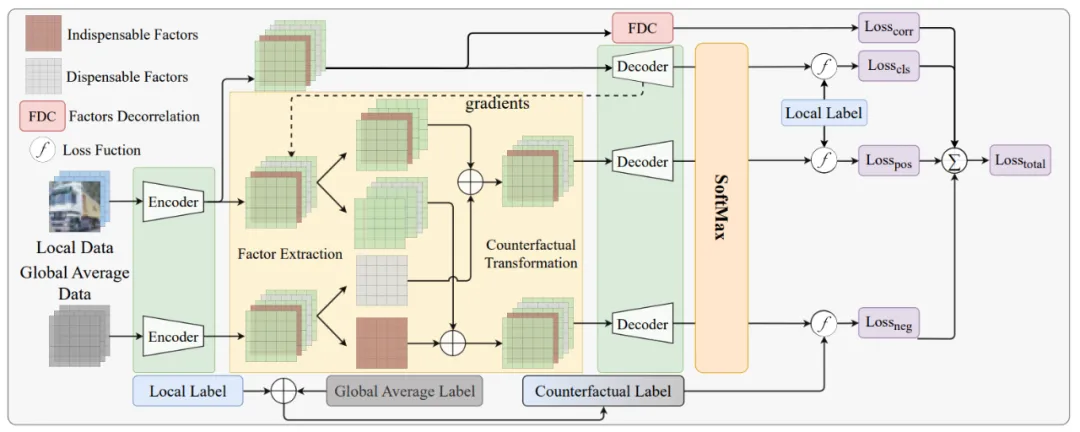
圖 3:FedCFA 中的本地模型訓練流程
FedCFA 中的本地模型訓練流程如圖 3 所示。反事實變換模塊的主要任務是在端側生成與全局數據分布對齊的反事實樣本:
- 特征提取:使用編碼器(Encoder)從原始數據中提取特征因子
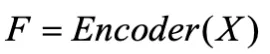 。
。 - 選擇關鍵特征:計算每個特征在解碼器(Decoder)輸出層的梯度,選擇梯度小 / 大的 topk 個特征因子作為可替換的因子,使用
 將選定的小 / 大梯度因子設置為零,以保留需要的因子
將選定的小 / 大梯度因子設置為零,以保留需要的因子 - 生成反事實樣本:用 Encoder 提取的全局平均數據特征替換可替換的特征因子,得到反事實正 / 負樣本,對于正樣本,標簽不會改變。對于負樣本,使用加權平均值來生成反事實標簽:
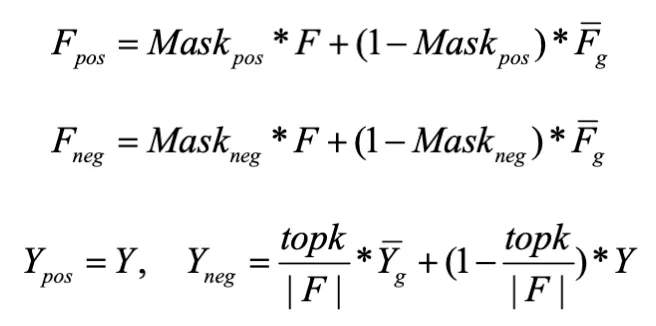
因子去相關損失
同一像素可能包含多個數據特征。例如,在動物圖像中,一個像素可以同時攜帶顏色和外觀信息。為了提高反事實樣本的質量,FedCFA 引入了因子去相關(Factor Decorrelation, FDC)損失,用于減少提取出的特征因子之間的相關性,確保每個特征因子只攜帶單一信息。具體來說,FDC 損失通過計算每對特征之間的皮爾遜相關系數(Pearson Correlation Coefficient)來衡量特征的相關性,并將其作為正則化項加入到總損失函數中。
給定一批數據,用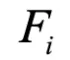 來表示第 i 個樣本的所有因子。
來表示第 i 個樣本的所有因子。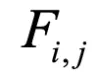 表示第 i 個樣本的第 j 個因子。將同一批次中每個樣本的相同指標 j 的因子視為一組變量
表示第 i 個樣本的第 j 個因子。將同一批次中每個樣本的相同指標 j 的因子視為一組變量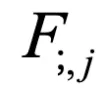 。最后,使用每對變量的 Pearson 相關系數絕對值的平均值作為 FDC 損失:
。最后,使用每對變量的 Pearson 相關系數絕對值的平均值作為 FDC 損失:
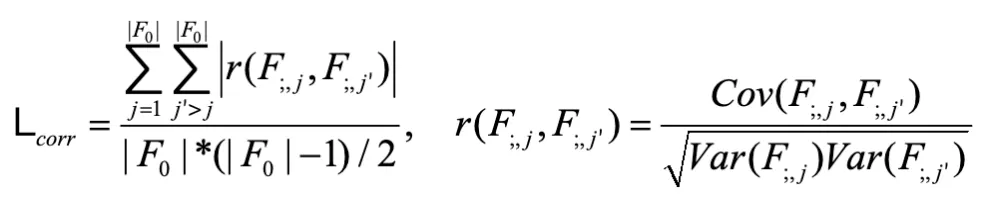
其中 Cov (?) 是協方差計算函數,Var (?) 是方差計算函數。最終的總損失為:
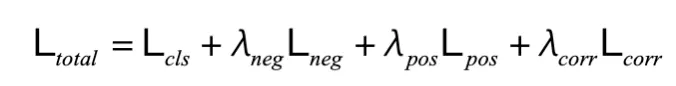
實驗結果
實驗采用兩個指標:500 輪后的全局模型精度 和 達到目標精度所需的通信輪數,來評估 FedCFA 的性能。
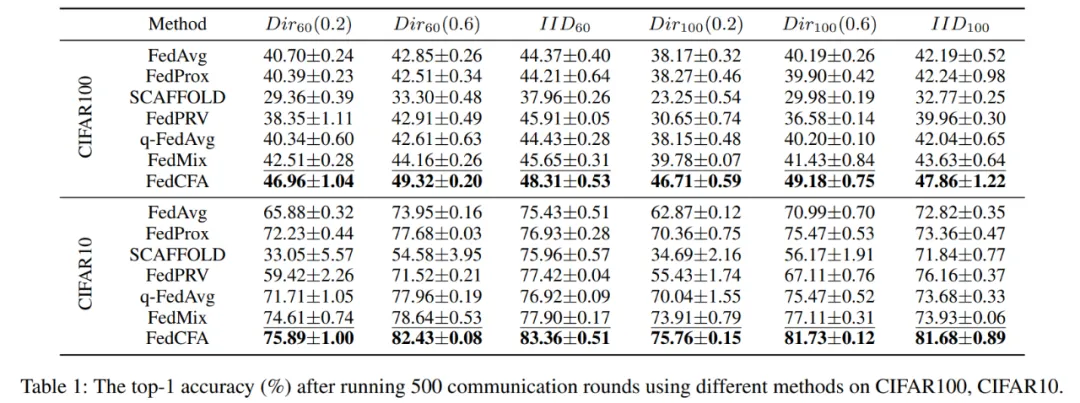
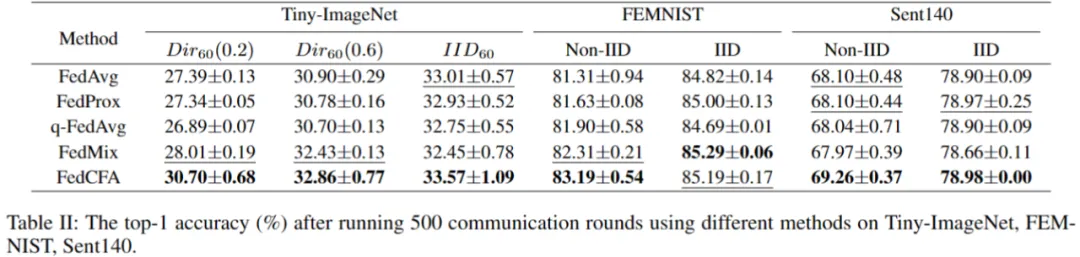

實驗基于 MNIST 構建了一個具有辛普森悖論的數據集。具體來說,給 1 和 7 兩類圖像進行上色,并按顏色深淺劃分給 5 個客戶端。每個客戶端的數據中,數字 1 的顏色都比數字 7 的顏色深。隨后預訓練一個準確率 96% 的 MLP 模型,作為聯邦學習模型初始模型。讓 FedCFA 與 FedAvg,FedMix 兩個 baseline 作為對比,在該數據集上進行訓練。如圖 5 所示,訓練過程中,FedAvg 和 FedMix 均受辛普森悖論的影響,全局模型準確率下降。而 FedCFA 通過反事實轉換,可以破壞數據中的虛假的特征 - 標簽關聯,生成反事實樣本使得本地數據分布靠近全局數據分布,模型準確率提升。

圖 4: 具有辛普森悖論的數據集
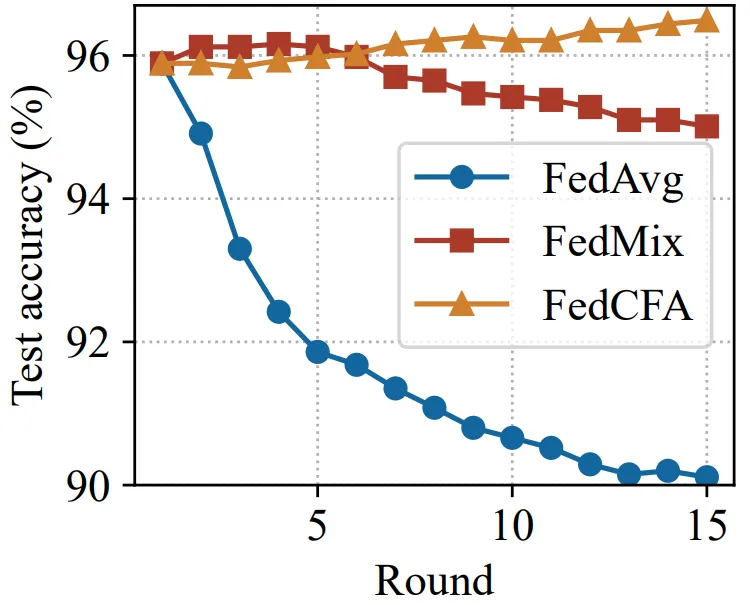
圖 5: 在辛普森悖論數據集上的全局模型 top-1 準確率
消融實驗

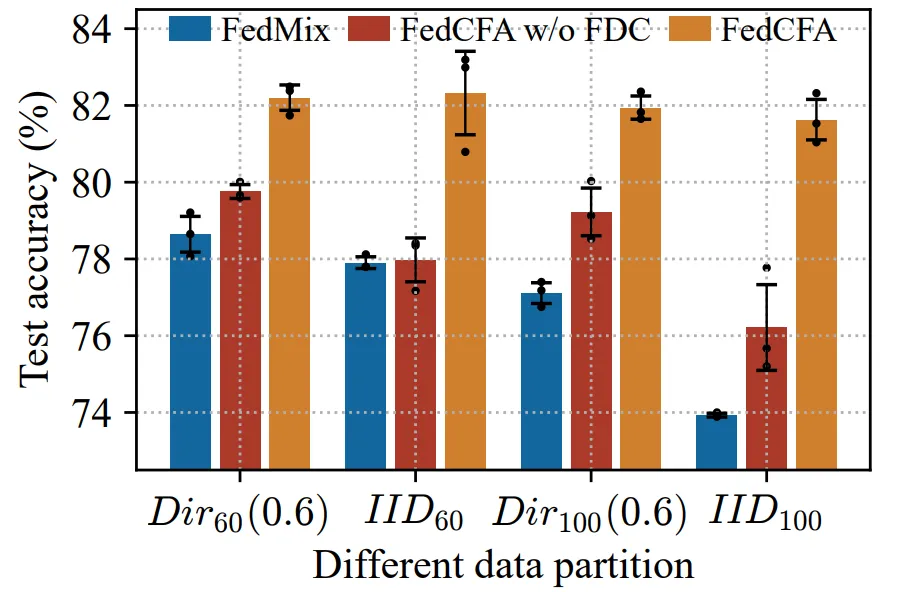
圖 6:因子去相關 (FDC) 損失的消融實驗








































