Meta-Chunking:通過邏輯感知學習高效的文本分段

本文是由人大提出的,旨在解決在檢索增強生成(RAG)系統中,文本分段這一關鍵方面被忽視的問題。具體來說,傳統文本分段方法(如基于規則或語義相似性)在捕捉句子間深層語言邏輯聯系方面存在不足,導致在知識密集型任務(如開放域問答)中的性能受到影響。本文通過引入Meta-Chunking的概念及其兩種實現策略(邊際采樣分段和困惑度分段),解決了以下幾個關鍵問題:
邏輯連貫性問題:
- 問題:傳統文本分段方法往往基于規則或語義相似性,難以捕捉句子間的深層邏輯聯系(如因果、過渡、并行和漸進關系)。
- 解決方案:Meta-Chunking通過利用LLMs的強大理解和推理能力,設計了邊際采樣分段和困惑度分段策略,精確識別文本分段邊界,確保分段后的文本塊具有邏輯連貫性。
資源和時間效率問題:
- 問題:現有的文本分段方法(如LumberChunker)需要使用高性能的LLMs(如Gemini模型),導致資源和時間成本顯著增加。
- 解決方案:邊際采樣分段有效減少了文本分段對模型大小的依賴,使推理能力相對較弱的小型語言模型也能勝任此任務。困惑度分段進一步提高了處理效率,實現了資源和時間的節省。
細粒度和粗粒度分段的平衡問題:
- 問題:僅通過調整閾值來控制塊大小有時會導致塊大小不均勻,難以滿足用戶的多樣化分段需求。
- 解決方案:提出了一種結合Meta-Chunking與動態合并的策略,旨在靈活應對不同的分段要求,在細粒度和粗粒度文本分段之間取得有效平衡。
長文本處理問題:
- 問題:處理較長文本時,傳統的分段方法可能導致上下文連貫性喪失或GPU內存溢出。
- 解決方案:在困惑度分段中引入鍵值(KV)緩存機制,在保持句子間邏輯連貫性的前提下計算困惑度,從而優化GPU內存和計算準確性。
跨語言適應性問題:
- 問題:小模型在跨語言適應性方面存在局限性,難以直接應用于多語言文本分段。
- 解決方案:通過實驗驗證,中等規模的模型(如1.5B參數級別)在處理不同長度的文本分段時能在性能和效率之間保持出色平衡。
通過上述解決方案,本文提出的Meta-Chunking方法顯著提升了基于RAG的單跳和多跳問答性能,同時在效率和成本節約方面表現出優越性能,解決了傳統文本分段方法在邏輯連貫性、資源和時間效率、細粒度和粗粒度分段平衡、長文本處理以及跨語言適應性等方面的不足。
Meta-Chunking
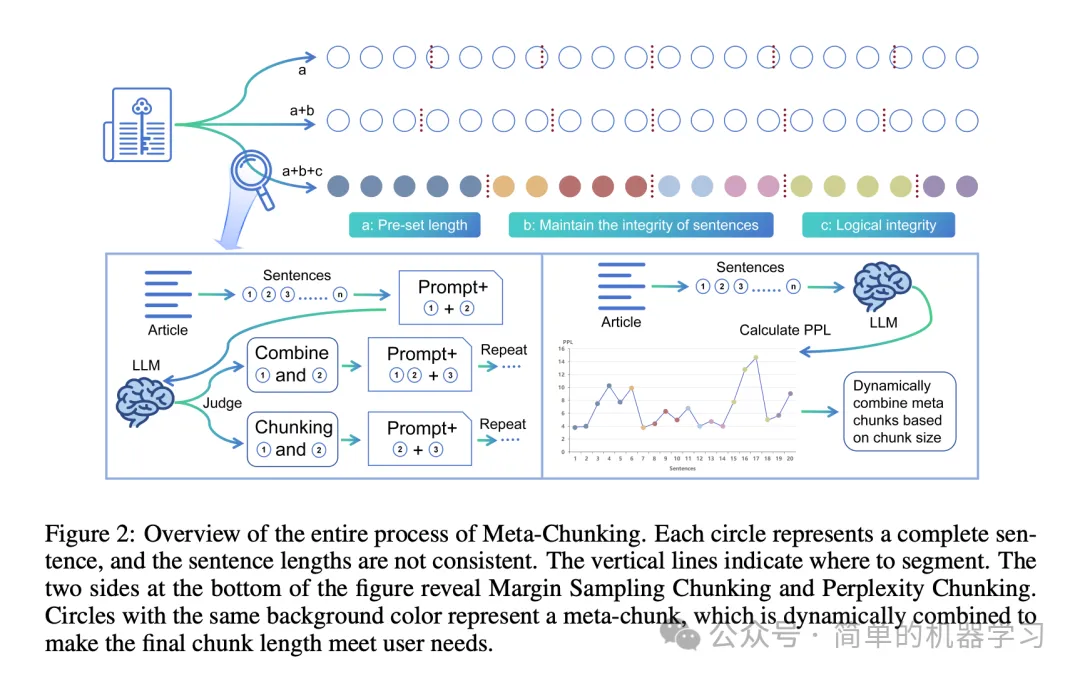
Meta-Chunking是一種創新文本分段技術,利用LLMs的能力靈活地將文檔分割成邏輯連貫的獨立塊。方法是基于一個核心原則:允許塊大小的可變性,以更有效地捕捉和保持內容的邏輯完整性。這種粒度的動態調整確保每個分段塊包含一個完整且獨立的表達,從而避免分段過程中邏輯鏈的中斷。這不僅增強了文檔檢索的相關性,還提高了內容清晰度。
如上圖所示,方法整合了傳統文本分段策略的優勢,如遵守預設塊長度約束和確保句子結構完整性,同時在分段過程中增強了保證邏輯連貫性的能力。關鍵在于引入了一個介于句子級和段落級文本粒度之間的新概念:Meta-Chunking。一個元塊由段落中順序排列的句子集合組成,這些句子不僅共享語義相關性,更重要的是包含深層語言邏輯聯系,包括但不限于因果、過渡、并行和漸進關系。這些關系超越了單純的語義相似性。為了實現這一目標,論文中設計和實現了以下兩種策略。
邊際采樣分段
給定一段文本,初始步驟將其分割成一系列句子,記為,最終目標是進一步將這些句子分割成若干塊,形成新集合,每個塊包含原始句子的連貫分組。該方法可以表述為:
其中表示二分類決策,表示在和之間形成指令,關于它們是否應合并,其中包含單個句子或多個句子。通過模型獲得的概率,我們可以推導出兩個選項之間的概率差異。隨后,通過將與閾值進行比較,可以得出兩個句子是否應分段的結論。對于的設置,我們最初將其賦值為0,然后通過記錄歷史的并計算其平均值進行調整。
困惑度分段
同樣,論文中將文本分割成句子,并使用模型計算每個句子基于前面句子的困惑度:
其中表示中的總token數,表示中的第個token,表示所有在之前的token。為了定位文本分段的關鍵點,算法進一步分析的分布特征,特別是識別最小值:
這些最小值被視為潛在的塊邊界。如果文本超出LLMs或設備的處理范圍,論文策略性地引入鍵值(KV)緩存機制。具體來說,文本首先根據token分成若干部分,形成多個子序列。隨著困惑度計算的進行,當GPU內存即將超過服務器配置或LLMs的最大上下文長度時,算法適當地移除先前部分文本的KV對,從而不會犧牲太多的上下文連貫性。
困惑度分段的理論分析
LLMs旨在學習一個分布¥Q¥,使其接近樣本文本的經驗分布。為了量化這兩個分布之間的接近程度,通常使用交叉熵作為度量。在離散場景下,相對于的交叉熵正式定義如下:
其中表示經驗熵,是和之間的Kullback-Leibler(KL)散度。LLMs的困惑度在數學上定義為:
需要注意的是,由于是不可優化的且有界,真正影響不同LLMs困惑度計算差異的是KL散度,它作為評估分布差異的度量。KL散度越大,兩個分布之間的差異越大。此外,高困惑度表明LLMs對真實內容的認知幻覺,這些部分不應被分段。
另一方面,Shannon(1951)通過函數近似任何語言的熵:
其中表示文本序列中的個連續token ,熵可以表示為:
然后,基于論文附錄A.1中的證明,對所有成立,可以推導出:
通過上面的公式可以觀察到對于大規模文本處理任務,增加上下文長度往往會降低交叉熵或困惑度,這一現象反映了LLMs在捕獲更廣泛的上下文信息后進行更有效的邏輯推理和語義理解的能力。
實驗
論文在十一個數據集上的廣泛實驗,驗證了Meta-Chunking策略在提升基于RAG的單跳和多跳問答性能方面的有效性。具體數據請參看原論文。
論文地址:https://arxiv.org/pdf/2410.12788
github: https://github.com/IAAR-Shanghai/Meta-Chunking