破案了！

就在剛剛，來自普林斯頓和谷歌的研究者發(fā)現(xiàn)——

大模型做數(shù)學題，不是靠推理，而是靠從訓練集里記下的解題技巧！

論文地址：https://arxiv.org/abs/2502.06453

這「未解之謎」一直困擾著不少業(yè)內(nèi)人士：在數(shù)學上，LLM到底是學會了舉一反三，還是只是學會了背題？

此前OpenAI o1-preview被爆出，數(shù)學題目稍作修改，正確率暴降30%！

之后，OpenAI用o3-mini證明了LLM的強大數(shù)學推理能力，但網(wǎng)上就有數(shù)據(jù)集中相同類型的題目，讓這一問題顯得更加撲朔迷離。

這次華人研究團隊帶來了新進展，推出了全新的MATH-Perturb測試基準，測試AI泛化能力到底如何。

隨著LLM在MATH、OlympiadBench和AIME上連破紀錄，這讓人們看到了AI在數(shù)學領域的巨大潛力。

「數(shù)學天才」頭腦的背后，模型是真的模型理解了數(shù)學知識、掌握了推理精髓，還是只是表面上的「記憶游戲」？

如果模型在訓練時接觸到了與測試集相似的題目，那它在測試中的高準確率可能就有「水分」，很可能只是記住了答案，而非真正理解了解題思路。

就像一個學生，靠死記硬背記住了課本上的例題答案，一旦考試題目稍有變化，就不知道如何下手。

研究人員采用零樣本思維鏈（zero-shot chain-of-thought）的方法，對18種不同類型的LLM進行了全面測試。這些模型涵蓋了長思維鏈模型、閉源大模型、開源小模型以及數(shù)學專用模型等。

在MATH-P-Hard數(shù)據(jù)集上，測試的所有模型都遭遇了「滑鐵盧」，準確率普遍降低了10%-25%，包括OpenAI的GPT-4/o1系列、谷歌的Gemini系列以及Deepseek-math、Qwen2.5-Math等模型。

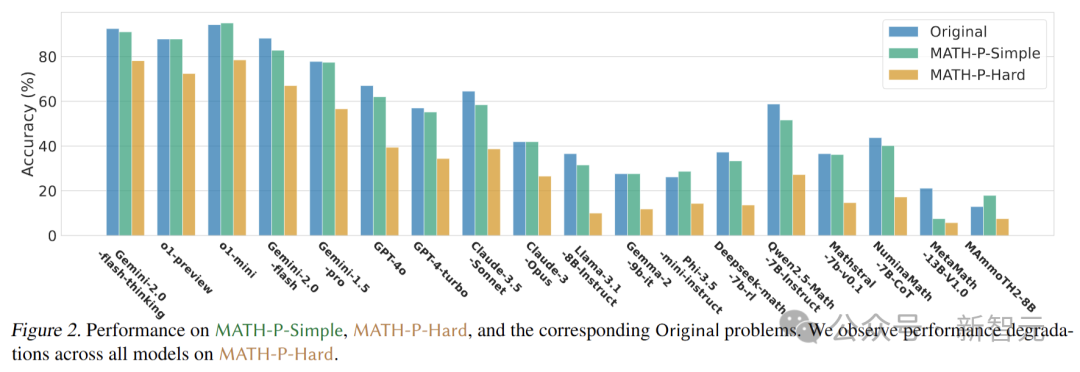
文章的主要結果如下：

1. 對18個LLM的數(shù)學推理能力進行了基準測試，結果顯示所有模型，包括o1-mini和Gemini-2.0-flash-thinking，在MATH-P-Hard上的性能顯著下降（10%-25%）。這表明這些模型偏向于原始推理模式的分布，并且面對硬擾動的問題時，會受到分布外效應的影響。
2. 對失敗模式分析的深入分析，并發(fā)現(xiàn)了一種新的記憶形式，即模型從訓練集中記憶了解題技巧，并在不判斷修改后的設置是否仍然適用的情況下盲目應用這些技巧。
3. 研究了使用相應的原始未修改問題和解決方案進行上下文學習ICL的影響，并證明在MATH-P-Hard上，使用原始示例的ICL可能會損害模型的表現(xiàn)，因為模型可能無法識別細微的差異，并被示例誤導。
4. 由12位研究生級別的專家策劃、設計并構建了 MATH-P-Simple（簡單擾動）和 MATH-P-Hard（硬擾動）兩個數(shù)據(jù)集，自MATH數(shù)據(jù)集的第5級（最難）問題。

這不由得讓人想起之前蘋果研究者的一篇廣為流傳的論文。

論文地址：https://arxiv.org/abs/2410.05229

他們發(fā)現(xiàn)，給數(shù)學題換個皮，LLM本來會做的數(shù)學題，就忽然不會了！

「當索菲照顧她侄子時，她會為他拿出各種各樣的玩具。積木袋里有31塊積木。毛絨動物桶里有8個毛絨動物。堆疊環(huán)塔上有9個五彩繽紛的環(huán)。索菲最近買了一管彈性球，這使她為侄子準備的玩具總數(shù)達到了62個。管子里有多少個彈性球？」把這道題中索菲的名字、侄子的稱謂、玩具的具體數(shù)目改變，模型就做不對了

只修改了題目中的專有名詞，LLM的表現(xiàn)就明顯出現(xiàn)了分布均值從右向左的移動，方差增加，也就是說，它們做題的準確度變低了。

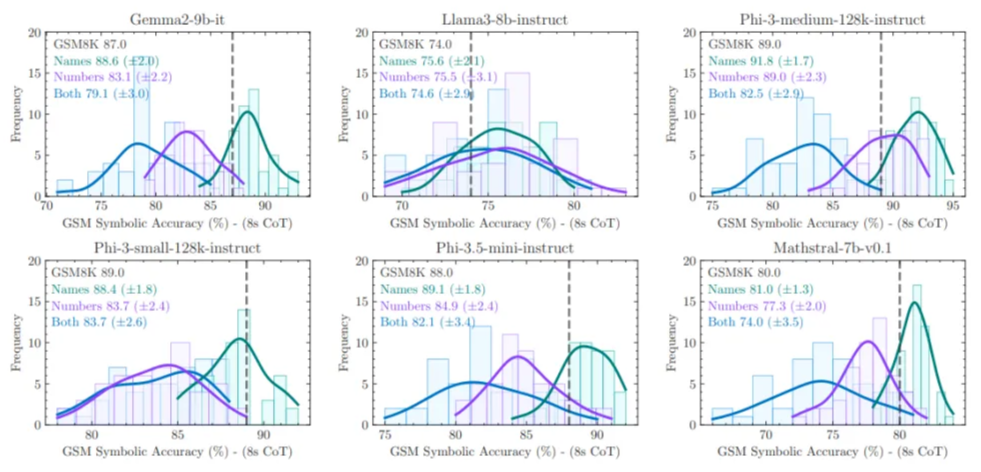
這次普林斯頓、谷歌的這項研究，也再次驗證了這篇論文的觀點：LLM對數(shù)學題的推理能力，有水分。

MATH-Perturb：數(shù)學推理能力的「試金石」

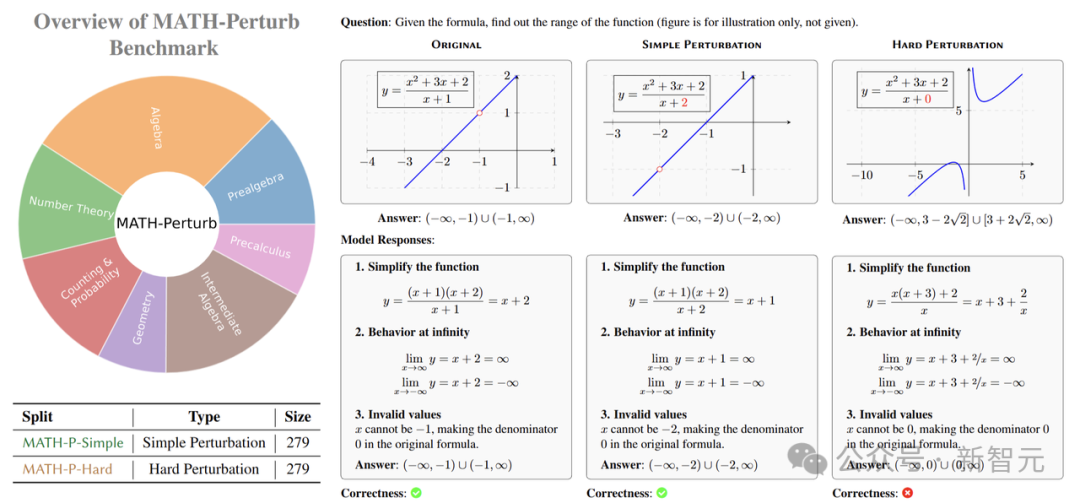
為了更準確地評估LLM的數(shù)學推理能力，研究人員推出了MATH-Perturb基準測試，用來檢驗模型在面對不同難度擾動時的表現(xiàn)。

這個基準測試包含兩個部分：MATH-P-Simple和MATH-P-Hard，題目均來自MATH數(shù)據(jù)集中難度最高的5級問題。

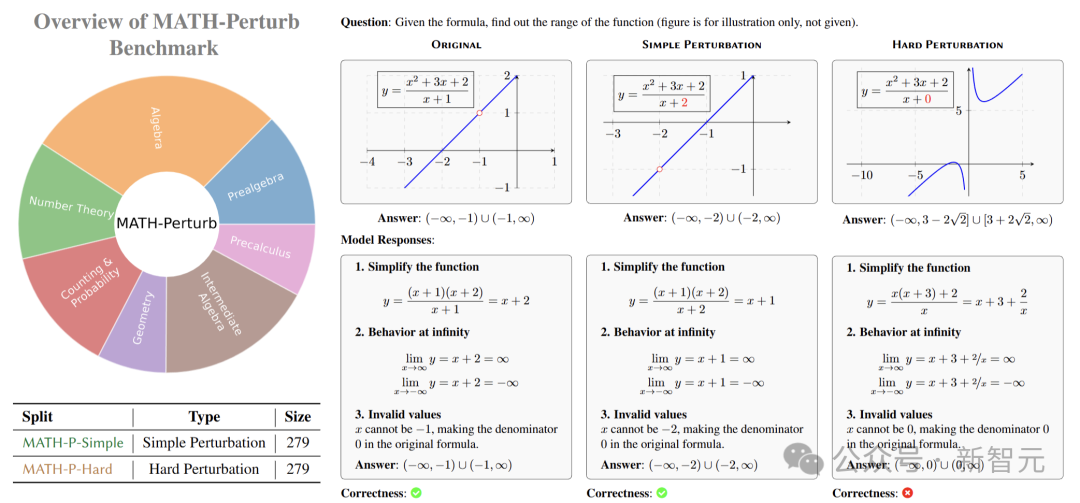
在構建數(shù)據(jù)集時，研究人員邀請了12位具有深厚數(shù)學背景的數(shù)學大佬來擔任注釋者。

對于MATH-P-Simple，注釋者進行的是簡單擾動，對原問題進行一些非本質(zhì)的修改，例如改變問題中的數(shù)值、變量名稱或表述方式，但不改變問題的基本推理模式和解題方法。

比如，原問題是求函數(shù)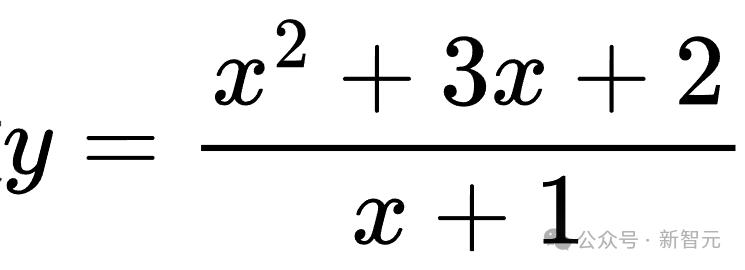的值域，經(jīng)過簡單擾動后，變成求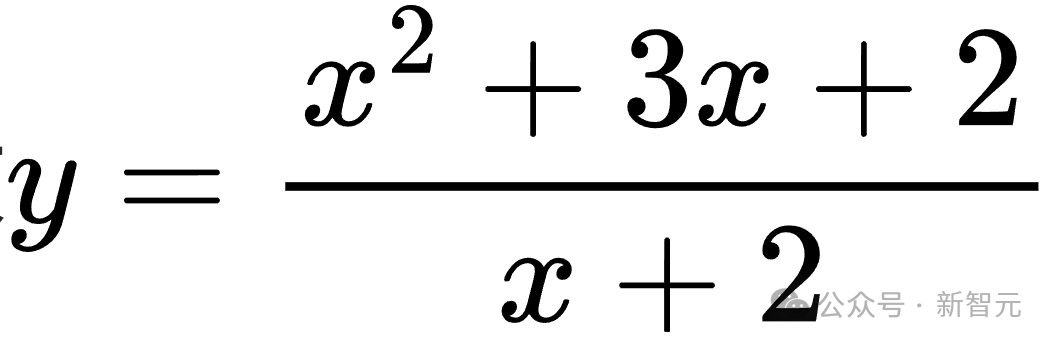的值域。雖然題目有所變化，但解題的核心思路還是通過因式分解和分析函數(shù)特性來求解。

MATH-P-Simple和MATH-P-Hard的標注過程

硬擾動（MATH-P-Hard）則是對原問題進行小而關鍵的修改，這些修改會導致原有的解題方法不再適用，需要運用更高級的數(shù)學知識和更復雜的推理技巧來解決。

同樣以函數(shù)值域問題為例，硬擾動后的問題可能變成求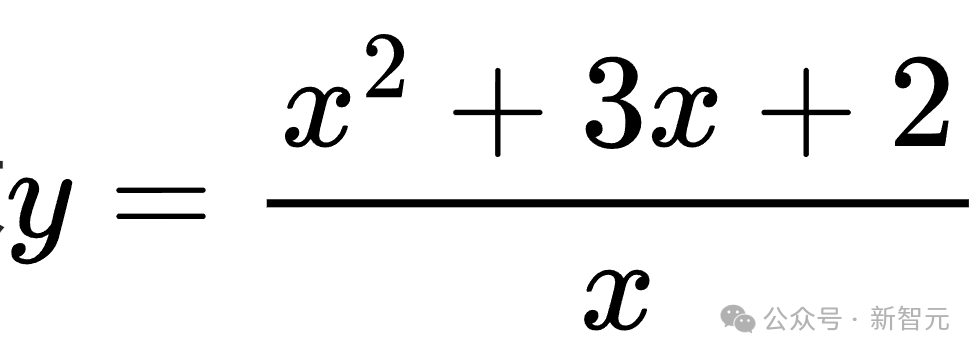的值域，這時就需要運用柯西-施瓦茨不等式等更復雜的數(shù)學知識來求解。

果然，這樣修改后，LLM就露出馬腳了！

它們并沒有發(fā)現(xiàn)，原先自己學會的解題技巧，并不適用于修改后的數(shù)學題，而是繼續(xù)盲目套用。

比如這道題中，數(shù)學題中具體條件改變后，模型仍然采用了原先的解法，最終當然就得出了錯誤的答案。

（更多具體情況，參見實驗結果）

此外，研究人員還遵循了兩個重要原則。

「最小修改」原則要求注釋者盡量減少對原問題的修改，這樣能在保持問題形式相近的情況下，測試模型的泛化能力。

「答案改變」原則保證修改后的問題答案與原答案不同，防止模型直接輸出記憶中的答案，確保結果真實可靠。

構建完數(shù)據(jù)集后，研究人員對每個擾動后的問題進行了仔細檢查，確保問題的表述清晰、準確，并且答案正確。

擾動問題與原始問題之間的歸一化編輯距離和嵌入向量余弦相似度分布情況如下圖所示。

詳細結果

研究人員采用零樣本思維鏈作為在基準測試中的標準評估方法。

為了進行對比，還會在原始的279個問題集上對模型進行評估，以下小節(jié)中將其稱為「原始」(Original)。

測試不允許使用任何工具，包括訪問代碼解釋器，因為發(fā)現(xiàn)許多問題可以通過編寫暴力搜索程序輕松解決。

為了檢查生成的答案是否與真實答案相匹配，采用了等價性檢查方法：首先進行字符串規(guī)范化，然后使用sympy包檢查兩個數(shù)學對象的等價性。

LLM的基準測試性能

考慮了多種語言模型，包括長思維鏈（long-CoT）模型、閉源的大型模型、開源的小型模型以及專門針對數(shù)學的模型。其中具體分類如下：

• 長思維鏈（long-CoT）模型：o1-preview，o1-mini，Gemini 2.0 flash thinking
• 閉源模型：GPT-4o，GPT-4 Turbo（Achiam等，2023），Gemini 1.5 Pro，Gemini 2.0 flash，Claude 3.5 Sonnet，Claude 3 Opus（Anthropic, 2024）
• 開源通用模型：Llama 3.1，Gemma 2，Phi-3.5
• 數(shù)學專用模型：MetaMath，MAmmoTH2，Deepseek-Math，Qwen2.5-Math，NuminaMath，Mathtral

下表報告了LLM在原始問題集、MATH-P-Simple和MATH-P-Hard上的整體準確率，并分別計算了來自訓練集和測試集的準確率。

如預期的那樣，評估的所有模型在MATH-P-Hard上的表現(xiàn)顯著低于原始問題集，表明MATH-P-Hard更加困難。

同時，相較于原始問題集，大多數(shù)模型在MATH-P-Simple上的表現(xiàn)也略有下降。

作者注意到，性能下降主要來自訓練集。即便測試樣本與訓練問題具有相同的推理模式，最先進的模型也仍然存在泛化誤差。

對于來自測試集的問題，理想情況下，原始問題和MATH-P-Simple修改版，對模型來說應當是同樣「從未見過」的。

根據(jù)表1中的實驗證據(jù)，觀察到不同的結果：多個模型性能下降超過了5%；不過，令人驚訝的是，Phi-3.5-mini-instruct的表現(xiàn)反而有所提升。對于評估的大多數(shù)模型，MATH-P-Simple測試集的準確率接近原始測試集的準確率。

值得一提的是，盡管已有研究發(fā)現(xiàn)經(jīng)過修改的基準與原始基準之間，模型的性能下降幅度為58%到80%（測試的最佳模型是GPT-4），但在這次評估的模型中并未觀察到如此巨大的差距，這表明新開發(fā)的模型在應對簡單擾動時的魯棒性有所進展。

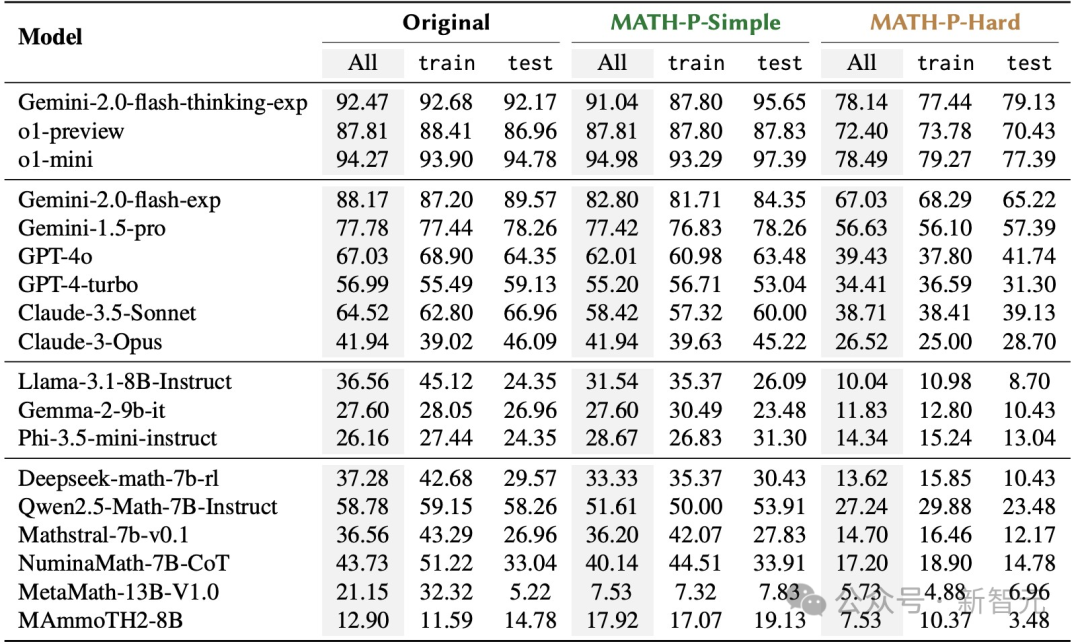
LLM零樣本思維鏈性能準確率：「Orignal」指的是未修改的279個問題集。對于train列和test列，分別報告來自訓練集和測試集的問題的準確率

推理時間擴展。已有研究表明，擴展推理時間計算可以提高LLM的性能。將推理時間擴展到基準測試的結果。

對于每個問題，獨立生成N個解答，并通過以下公式計算每個1≤k≤N的pass@k指標：

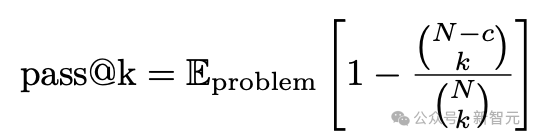
其中c是n次運行中正確答案的數(shù)量。

此外，還計算了自一致性，即多數(shù)投票法的表現(xiàn)。對于每個k，從N次運行中隨機抽取k個回答，并得到多數(shù)投票的答案。

下圖報告了5次隨機抽樣的平均值和標準差。對于Llama-3.1-8B-Instruct和Qwen2.5-Math-7B-Instruct，設置N = 64，而對于o1-mini，設置N = 8。

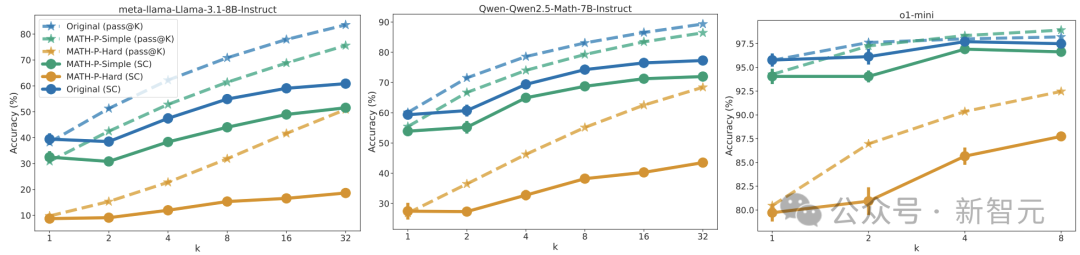
擴展推理時間計算的效果

LLM做數(shù)學題，會因為什么而失敗

為了研究模型在面對硬擾動時的泛化能力，作者集中分析了那些在MATH-P-Hard修改版中的失敗案例。

但要注意：總問題中的20%-47%，模型至少能正確解決原始問題或MATH-P-Simple修改版。

對于這些問題，可以使用較容易問題的正確解作為參考，更好地確定模型在困難問題中的失敗模式。

首先，觀察到當模型面對更難的問題時，普遍存在一些失敗模式。這些錯誤在較弱的模型中表現(xiàn)得尤為突出。

除了常見的失敗模式外，當比較MATH-P-Hard修改版的錯誤解與較容易版本時，能夠識別出一定數(shù)量的記憶化問題。

具體來說，模型可能忽略修改后的假設，錯誤地假設原始假設仍然成立。

例如，參見圖5中的示例。原問題為：

問題：十個人圍坐在一張圓桌旁。隨機抽取其中三個人做演講。被選中的三個人坐在連續(xù)座位上的概率是多少？

修改后，問題變難了：

十個人圍坐在一個圓桌旁，隨機選擇三個人以特定順序進行演講。問這三個人中，第一個和第二個演講者坐在連續(xù)座位上，并且第二個和第三個演講者也坐在連續(xù)座位上的概率是多少？

模型并沒有意識到問題已經(jīng)改變，原來的推理方法不再有效。然后按照原來的推理模式進行推理，給出了原題的答案——1/12。

而實際上，正確答案是應該是1/36。

作者手動進行了20次重復發(fā)現(xiàn)Claude-3.5-Sonnet的通過率為50%。在錯誤中，30%是由于上述記憶問題造成的。

記憶化與錯誤推理結合的示例

在其他情況下，模型可能盲目地應用原始問題的解題技巧，而沒有首先判斷這些技巧在修改后的問題環(huán)境中是否仍然適用（圖1中的回答就是由GPT-4o生成的一個例子）。

有趣的是，模型甚至可能輸出原始問題的預期結果（并未在上下文中提供），而不是修改版問題的結果。

比如上面這道題吧，原題是如果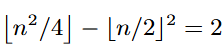并找出所有滿足條件的整數(shù)n。

而改變后的題將條件替換為并要求找出滿足條件的最小整數(shù)n。

結果在這種情況下，模型給出的答案卻是所有整數(shù)值（10和13），而非最小整數(shù)值（10）。

誒，這是模型背答案實錘了？

要知道，這種記憶化行為對于大多數(shù)現(xiàn)有文獻中的擾動類型來說是難以捕捉的，因為這些擾動并不需要不同的解題策略。

模式崩潰

研究人員還關注了模式崩潰（pattern collapse）帶來的影響。

模式崩潰是指模型無法區(qū)分擾動后的問題和原問題，導致回答與原問題答案相同。

在MATH-P-Hard數(shù)據(jù)集中，除了少數(shù)幾個模型外，模式崩潰的情況在總錯誤中的占比不到10%。

這表明，模型在面對硬擾動問題時，雖然可能會出現(xiàn)各種錯誤，但多數(shù)情況下還是能夠意識到問題的變化，而不是簡單地重復原答案。

然而，人工檢查發(fā)現(xiàn)，模型的輸出往往不是簡單地重復原答案，而是在推理過程中出現(xiàn)了一些微妙的錯誤，例如忽略或誤解修改后的假設。

上下文學習

上下文學習是指模型在推理時利用原問題和答案作為示例來輔助解題。

在MATH-P-Simple數(shù)據(jù)集上，使用原問題和答案作為上下文學習示例，幾乎能提升所有模型的性能。

這是因為MATH-P-Simple問題可以通過直接應用原解題步驟來解決，原問題和答案的示例能提供有用的線索。

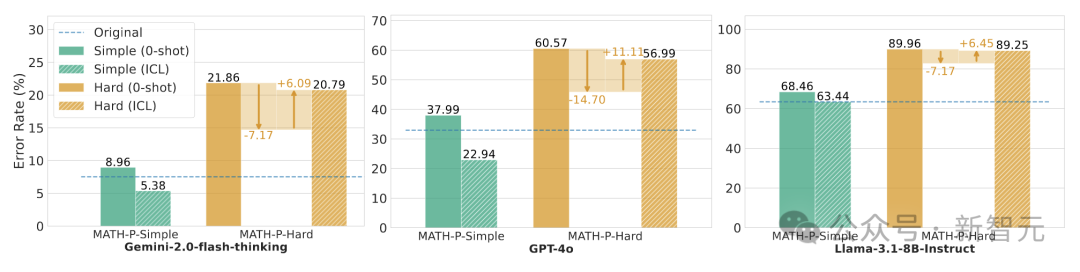
然而，在MATH-P-Hard數(shù)據(jù)集上，上下文學習的效果則較為復雜。

雖然原答案中的數(shù)學知識有時能夠幫助模型解決修改后的問題，但由于原問題和MATH-P-Hard問題之間存在微妙的差異，模型也容易被原答案誤導，導致錯誤增加。

總體來看，上下文學習在MATH-P-Hard上的效果并不理想，提升幅度非常有限。

LLM在面對硬擾動問題時，表現(xiàn)出明顯的局限性，許多錯誤源于模型對解題技巧的盲目記憶，而缺乏對問題本質(zhì)的理解。

總之，這項研究顯示，所有模型在復雜擾動MATH-P-Hard 上的表現(xiàn)均有所下降，而且許多錯誤都是源于一種新的記憶形式——

模型從訓練集中記住了解題技巧，然后在題目改變條件后，并不判斷是否適用，而盲目應用這些技巧。

這說明，雖然大多數(shù)LLM在數(shù)學推理方面取得了一定的成績，但距離真正理解和掌握數(shù)學知識還有很大的差距。

不過最近，谷歌DeepMind拿下IMO金牌的AlphaGeometry，首次破解了2009年IMO最難幾何題G7。

在過程中，它給出了石破天驚的驚人解法——

利用關鍵的輔助作圖（圖中的紅點），就只需求「角度」和「比例推導」。

所以，o1-preview、o1-mini、GPT-4o、Deepseek-Math等模型，在解數(shù)學題上和AlphaGeometry究竟相差多遠呢？

這就讓人十分期待，接下來這個領域的更多研究了。