生成AI的兩大范式:擴散模型與Flow Matching的理論基礎與技術比較
生成模型已成為人工智能領域的關鍵突破,賦予機器創建高度逼真的圖像、音頻和文本的能力。在眾多生成技術中,擴散模型和Flow Matching尤為引人注目。這兩種方法雖然都致力于在噪聲與結構化數據之間建立轉換,但其基礎原理存在本質區別。本文將系統地比較這兩種先進技術,深入探討其數學原理、實際應用及理論解釋。
基本原理
在深入數學分析前,有必要從直觀層面理解這兩種方法的核心概念:
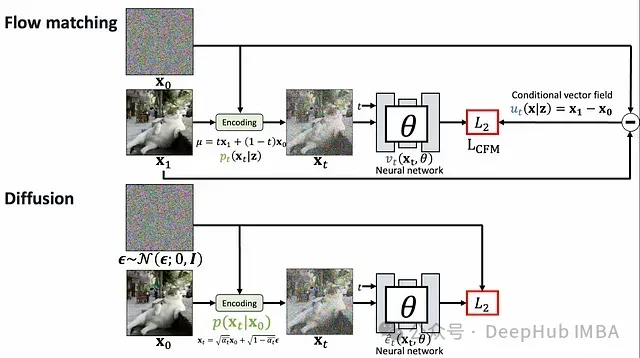
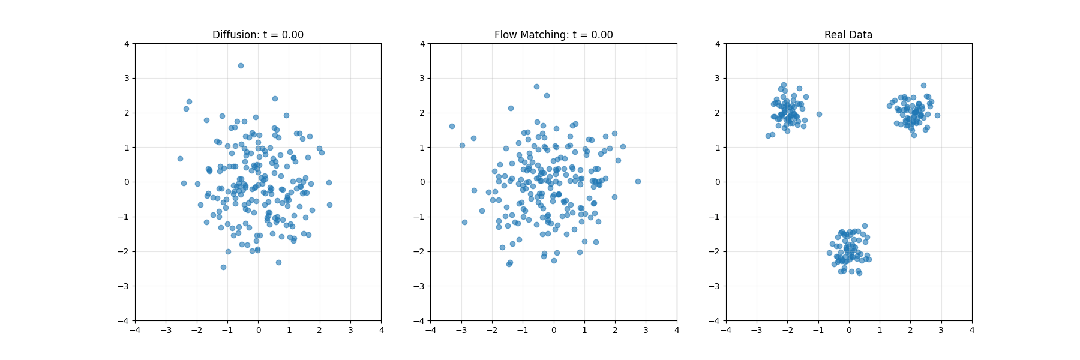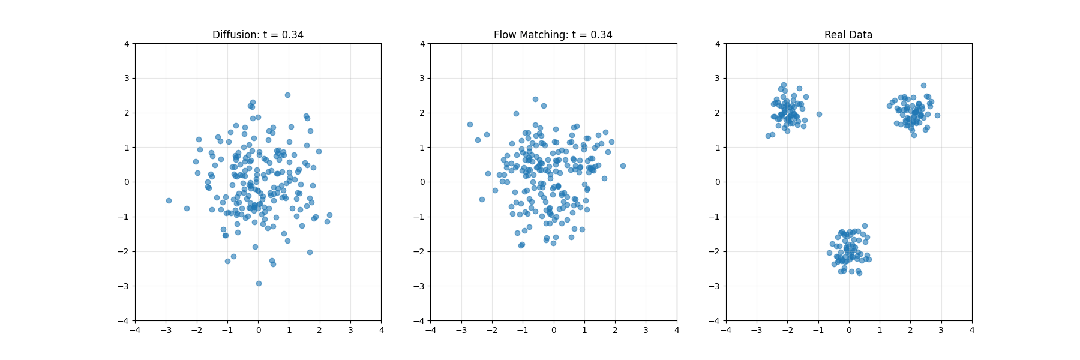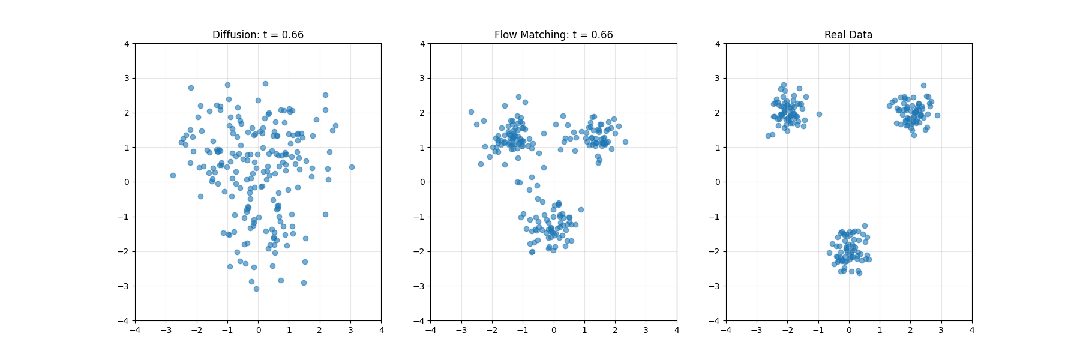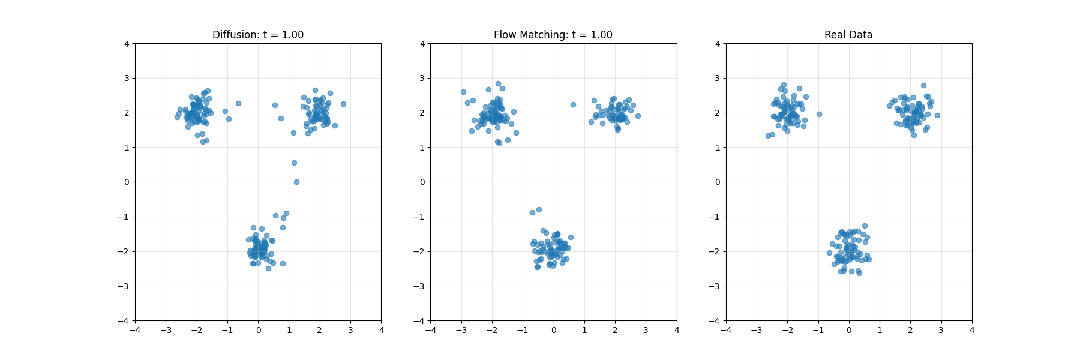
擴散模型系統性地向數據添加噪聲,直至將其轉化為純粹的隨機噪聲,然后學習此過程的逆向轉換。這一過程可類比為將照片逐步溶解至完全模糊狀態,隨后從模糊中重建原始影像的過程。
Flow Matching則構建噪聲分布與數據分布間的連續路徑(流)。這一過程可類比為定義一種平滑的轉換計劃,使隨機噪聲逐漸形成有結構的數據,如同觀察一塊黏土從無序狀態被塑造成精細雕像的過程。
擴散模型的數學基礎
前向過程
擴散模型定義了一個前向過程,該過程在 T 個時間步長內有序地向數據 x_0 添加高斯噪聲:
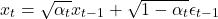
其中
且 \alpha_t \in (0, 1) 表示噪聲調度參數。
此過程可通過隨機微分方程(SDE)表示:
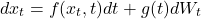
其中 W_t 代表標準維納過程(布朗運動),f(x_t, t) 為漂移系數,g(t) 為擴散系數。
經過充分的擴散步驟,x_T 將近似標準正態分布 \mathcal{N}(0, I),原始數據的結構信息基本完全消散。
反向過程
擴散模型的核心在于學習逆轉噪聲添加過程,通過從隨機噪聲開始并迭代去噪來生成新數據。
反向過程定義為:
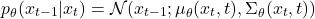
在實際應用中,諸如DDPM(去噪擴散概率模型)等模型針對每一時間步預測噪聲分量 \epsilon_\theta(x_t, t),進而推導出 \mu_\theta(x_t, t)。
訓練目標
擴散模型的訓練目標通常基于負對數似然的變分上界:

實踐中,這一目標函數常簡化為經重新加權的均方誤差:
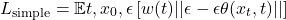
Flow Matching 的數學基礎
連續歸一化流與速度場
Flow Matching建立在連續歸一化流(CNF)的理論之上,CNF通過微分方程將一個概率分布轉換為另一個:
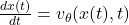
其中 v_\theta 表示可學習的速度場。
速度場的理解
速度場是一個為時空中每個點分配速度向量的函數,可類比為風向圖,指示了粒子在任一位置應移動的方向與速度。在生成模型語境下:
數學定義:速度場
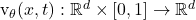
為時間 t 的每個點 x 分配一個向量 v。
物理理解:可想象為河流中任一點的水流方向與強度,決定了漂浮物體的運動軌跡。
變換特性:通過從 t=0 到 t=1 追蹤速度場,可以得到樣本從源分布(通常為噪聲)到目標數據分布的轉換路徑。
速度場具有以下關鍵特性,使其成為生成建模的有力工具:
- 確定性路徑:從給定起點追蹤速度場會產生確定性軌跡
- 可逆性:通過反轉速度向量可實現過程的逆向運行
- 概率質量守恒:連續性方程確保轉換過程中概率質量既不創生也不消失
速度場可視化可理解為網格上每點的方向矢量:
↑ ↗ → ↗ ↑
↖ ↑ ↑ → ↗
← ↙ ↑ ↑ →
↙ ↓ ↓ ↗ ↑
↓ ↙ ← ← ↑在Flow Matching中,通過神經網絡學習預測給定位置和時間的速度向量,該網絡經訓練以匹配定義分布間所需流的參考向量場。
概率流ODE
概率密度在流下的演化遵循連續性方程:
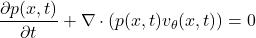
這一方程確保了變換過程中的質量守恒。
Flow Matching原理
Flow Matching的關鍵創新在于直接監督速度場 v_\theta,利用預定義的分布間路徑。此方法避開了從復雜的概率流方程推導速度場,而是直接約束速度場匹配參考向量場 u(x,t),后者定義了樣本的移動方式:
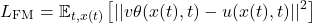
其中 x(t) 從路徑分布 p_t(x) 采樣,該分布在噪聲分布 p_0(x) 與數據分布 p_1(x) 間插值。
條件Flow Matching
條件Flow Matching (CFM)作為重要擴展,構建了各數據點與噪聲樣本間的路徑:
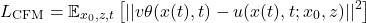
其中
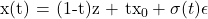
定義了噪聲 z 和數據 x_0 之間的路徑,
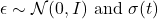
控制路徑噪聲水平。
主要差異分析
路徑定義
擴散模型通過添加高斯噪聲定義固定的隨機路徑。前向過程由預設的噪聲調度確定,模型學習逆轉這一特定過程。
Flow Matching則允許在分布間設計靈活路徑。這些路徑可為直線、曲線軌跡,甚至可動態學習,提供更大的設計自由度。
訓練動態
擴散模型通常需要估計復雜的概率密度或其替代量,導致訓練過程更具挑戰性,且對噪聲調度的精確設計有較高依賴。
Flow Matching直接監督速度場,形成更簡潔的均方誤差目標,訓練過程通常更為穩定。
采樣效率
擴散模型傳統上需要較多采樣步驟(通常1000步以上),盡管DDIM等技術已有所改進。
Flow Matching通常可利用高階ODE求解器,以較少步驟(10-100步)實現高質量采樣。
理論保證
擴散模型與基于分數的生成模型有深厚聯系,并提供明確的似然界限。
Flow Matching在特定條件下對精確密度匹配提供保證,為優化概率流ODE提供更直接路徑。
數值示例:轉換簡單分布
考慮將標準正態分布轉換為雙峰高斯混合分布的具體案例。
擴散方法
在擴散方法中,流程如下:
- 從目標分布(高斯混合)出發
- 按照調度 \beta_t 逐步添加噪聲
- 訓練模型預測每步噪聲
- 通過從純噪聲開始并迭代去噪進行采樣
對于一維示例,設定 T=10 步和線性噪聲調度 \beta_t = 0.1,前向過程為:

反向過程估計:
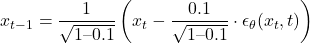
Flow Matching方法
Flow Matching方法流程為:
- 定義分布間路徑,例如線性插值:
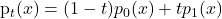
- 推導或定義誘導該路徑的速度場 u(x, t)
- 訓練模型預測此速度場
- 通過求解ODE:dx/dt = v_\theta(x, t) 從噪聲采樣到數據
對于簡單示例,假設直線路徑,速度場可表示為:
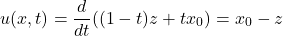
其中 z 為噪聲樣本,x_0 為數據樣本。
實踐實現與應用
擴散模型的實踐
具有代表性的擴散模型實現包括:
- DDPM (去噪擴散概率模型):奠定基礎的先驅模型
- DDIM (去噪擴散隱式模型):通過確定性過程加速采樣
- Stable Diffusion:應用于潛在空間提升圖像生成效率
- Imagen與DALL-E 2:基于擴散原理的文本到圖像生成系統
實現關鍵代碼示例:
# filepath: example.py
# Simplified DDPM training loop
def train_step(self, x_0, optimizer):
"""Single training step for diffusion model"""
batch_size = x_0.shape[0]
# Sample random timesteps
t = torch.randint(0, self.n_timesteps, (batch_size,), device=self.device, dtype=torch.long)
# Add noise to data
x_t, noise = self.q_sample(x_0, t)
# Predict noise
predicted_noise = self.model(x_t, t / self.n_timesteps)
# Compute loss
loss = F.mse_loss(noise, predicted_noise)
# Update parameters
optimizer.zero_grad()
loss.backward()
optimizer.step()
return loss.item()Flow Matching的實踐
代表性Flow Matching實現包括:
- 條件Flow Matching (CFM):高效訓練生成建模的神經ODE
- 一致性模型(Consistency Models):融合Flow Matching與擴散原理
- SiT (Score in Time):將擴散模型重構為插值匹配框架
實現關鍵代碼示例:
# filepath: example.py
# Simplified Flow Matching training loop
def train_step(self, x_0, optimizer):
"""Single training step for flow matching"""
batch_size = x_0.shape[0]
# Sample random timesteps
t = torch.rand(batch_size, device=self.device)
# Sample noise points
z = torch.randn_like(x_0)
# Get path points and target velocities
x_t, target_v = self.sample_path_point(x_0, z, t.unsqueeze(-1))
# Predict velocity vectors
predicted_v = self.model(x_t, t)
# Compute loss
loss = F.mse_loss(predicted_v, target_v)
# Update parameters
optimizer.zero_grad()
loss.backward()
optimizer.step()
return loss.item()概念類比
擴散模型:侵蝕與重建過程
擴散模型可類比為海灘上沙堡的侵蝕與重建。前向過程如同潮水逐漸沖刷沙堡,直至形成平坦沙面;反向過程則是學習如何通過理解沙粒運動規律,從平坦沙面重建精細結構。
Flow Matching:矢量場導航
Flow Matching類似于空間導航系統,在任一位置提供指向目標的方向矢量。無需遵循預設路線,學習的矢量場能從任意起點引導系統抵達目標分布。
方法融合與發展
近期研究顯示擴散模型與Flow Matching存在深層聯系:
- 概率流ODE:擴散過程可轉換為類似Flow Matching的確定性ODE
- 基于分數的方法:兩種方法可視為對數密度梯度(分數函數)的不同參數化
- 插值匹配:統一框架下整合多種生成方法
計算效率比較
擴散模型在采樣過程中通常需要更多的函數評估,導致計算成本相對較高。然而,這類模型可以使用相對簡化的架構和損失函數進行訓練,在實現復雜度方面具有一定優勢。
Flow Matching則通過采用復雜的ODE求解器實現更高的采樣效率,但精確建模速度場可能需要更為復雜的網絡架構設計。兩種方法的計算效率取舍主要體現在采樣速度與模型復雜度之間的平衡。
樣本質量分析
兩種方法均能達到先進的樣本生成質量,選擇應基于具體應用需求進行評估。擴散模型在處理高度結構化數據(如高分辨率圖像和復雜音頻)方面表現出色;而Flow Matching則在處理相對簡單的分布或對采樣速度有嚴格要求的場景中展現出明顯優勢。實際應用中,需權衡模型復雜度、訓練穩定性、采樣效率及質量要求等多方面因素。
總結
擴散模型與Flow Matching代表了生成建模領域的兩類重要技術范式,各自基于獨特的數學原理與實現策略。擴散模型通過定義固定的隨機過程并學習其逆轉,而Flow Matching則直接學習能夠沿靈活路徑轉換分布的速度場。從某種意義上說,Flow Matching保留了擴散模型的核心優勢,同時通過消除前向噪聲過程的限制實現了技術簡化。
深入理解這兩種方法間的差異與聯系,不僅有助于更全面把握生成建模的技術全貌,也為這一快速演進領域的發展提供了理論基礎和研究方向。