如果大語言模型（LLMs）能夠發(fā)現(xiàn)并糾正自己的錯誤，那豈不是很好？

而且，如果能夠直接從預(yù)訓(xùn)練中實現(xiàn)這一點，而無需任何監(jiān)督微調(diào)（SFT）或強化學(xué)習(xí)（RL），那會怎樣呢？

最新提出的離散擴(kuò)散模型，稱為GIDD，它能夠做到這一點。

在語言建模中，GIDD實現(xiàn)了計算效率匹配的最優(yōu)性能！

請注意：不是基于自回歸的LLM，是擴(kuò)散語言模型。

無條件生成與自我糾錯算法的比較

來自蘇黎世聯(lián)邦理工學(xué)院ETH Zurich等組織的研究團(tuán)隊，推廣了掩碼擴(kuò)散（masked diffusion），并推導(dǎo)出一系列廣義插值離散擴(kuò)散模型（general interpolating discrete diffusion，GIDD）的理論基礎(chǔ)。

GIDD不僅更靈活，而且在理論上得到了證據(jù)下界（evidence lower bound，ELBO）的閉式解。

實驗結(jié)果表明：GIDD樣本質(zhì)量（生成困惑度，PPL）最高可提升55%。

GIDD核心主要有3大特征：

1、推廣性強：GIDD適用于多種擴(kuò)散過程，不局限于掩碼擴(kuò)散。 

2、混合擴(kuò)散訓(xùn)練：訓(xùn)練了一個結(jié)合掩碼（masking）和均勻噪聲（uniform noise）的混合擴(kuò)散模型。 

3、雙重能力：不僅可以填補空缺（填充被掩蓋的token），還可以評估已填充token的正確性，并在必要時用更合理的 token替換錯誤的部分。

論文鏈接：https://www.arxiv.org/abs/2503.04482

項目地址：https://github.com/dvruette/gidd/

預(yù)測下一個token，雖然成果顯著，但存在固有的局限性，例如無法修改已經(jīng)生成的token。

這促使研究者探索替代方法，如離散擴(kuò)散。

然而，由于簡單性和有效性，掩碼擴(kuò)散（masked diffusion）成為流行選擇，但重新引入了無法修改token的這種局限性。

基于對擴(kuò)散模型添加噪聲的重要性認(rèn)識，新研究旨在探索離散擴(kuò)散模型的設(shè)計空間，并嘗試不同的擴(kuò)散過程。

廣義插值離散擴(kuò)散（GIDD）是新的離散擴(kuò)散方法，將掩碼擴(kuò)散推廣到任意插值噪聲過程。

在擴(kuò)散過程中，GIDD可以在任何時刻靈活地選擇添加不種類型的噪聲。

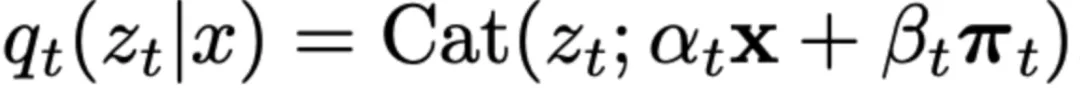
有趣的是，任何邊際分布符合上述方程的擴(kuò)散過程，都可以推導(dǎo)出證據(jù)下界（ELBO）。

想要掩碼擴(kuò)散？沒問題！

只需將 πt設(shè)為 one_hot([MASK])，然后在GIDD的ELBO上進(jìn)行訓(xùn)練即可。

不幸的是，掩碼擴(kuò)散無法進(jìn)行自我糾正。就像自回歸模型一樣，一旦token被確定，就無法再更改。

因此，如果模型在某個步驟出錯，就沒有辦法進(jìn)行修正。

為了解決這個問題，從BERT中汲取了靈感：如果除了掩碼token外，隨機用其他token替換一部分token，會怎么樣？

這樣，模型不僅需要學(xué)會「填空」，還要學(xué)會識別并修正錯誤的token。

由于GIDD的ELBO具有高度的靈活性，只需選擇合適的 πt來捕捉所需的動態(tài)特性。

設(shè)定 πt使得均勻噪聲的比例隨著噪聲水平的變化而上升或下降，并在 t=0.5時達(dá)到峰值。

真地有效嗎？

第一次實驗結(jié)果有些讓人失望，因為使用均勻噪聲訓(xùn)練的模型，其困惑度比僅使用掩碼的模型要差。

但考慮到這些模型除了需要填補缺失的token外，還要修正錯誤的token，這并不令人感到意外。

那樣本質(zhì)量又如何呢？

下圖發(fā)現(xiàn)發(fā)現(xiàn)生成性PPL（使用Gemma-2-9b測量）有了顯著的改進(jìn)，特別是對于使用均勻噪聲訓(xùn)練的模型來說更是如此，尤其是在推理預(yù)算緊張的情況下！

這是否意味著模型在糾正自己的錯誤呢？

為了弄清楚這一點，提出了一種自我糾正算法，通過一次修復(fù)一個token（使用模型）來改進(jìn)已經(jīng)生成的樣本，直到收斂到一個穩(wěn)定點。

這樣可以不斷提高樣本質(zhì)量（以生成PPL衡量），甚至超越僅僅通過增加去噪預(yù)算所能達(dá)到的水平，提供了一種簡單的方法來擴(kuò)展測試時計算資源！

值得注意的是，僅在去掩碼任務(wù)上訓(xùn)練的模型不具備這種能力。

在理論和實踐上，新研究的主要貢獻(xiàn)包括以下兩方面：

• 理論方面：將掩碼擴(kuò)散（masked diffusion）框架擴(kuò)展為「廣義插值離散擴(kuò)散」過程。GIDD能更靈活地選擇噪聲添加方式，同時仍然能夠得到累積狀態(tài)轉(zhuǎn)移和擴(kuò)散證據(jù)下界（ELBO）的閉式解。
• 實踐方面：基于理論分析，在實踐中取得了改進(jìn)。在計算資源相當(dāng)?shù)那闆r下，優(yōu)化訓(xùn)練目標(biāo)達(dá)到了當(dāng)前最優(yōu)的性能。同時，通過引入均勻噪聲，提高了樣本質(zhì)量，并實現(xiàn)了自校正能力（見圖1和表1）。

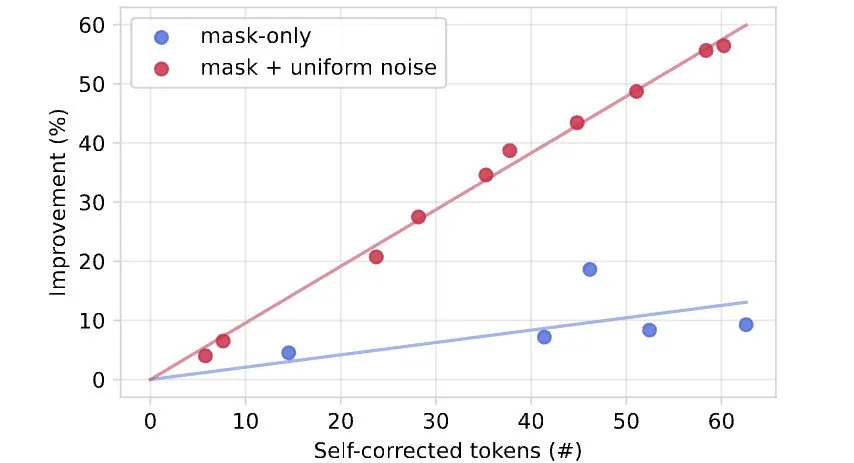
圖1.在訓(xùn)練過程中，使用GIDD結(jié)合掩碼和均勻噪聲，可以讓擴(kuò)散模型學(xué)會識別并糾正自身錯誤。

表1.使用20%均勻噪聲訓(xùn)練的GIDD+BASE模型進(jìn)行自我糾正的例子（綠色替換紅色）。

GIDD模型能夠在未明確訓(xùn)練的情況下糾正語法錯誤、改進(jìn)詞匯選擇，甚至提升事實準(zhǔn)確性。

自回歸模型缺陷

從觀察中提取世界的結(jié)構(gòu)是智能的基本機制。

生物體可以自然而然地做到這一點，而機器在這方面的能力直到最近才取得重大突破。

近年來，深度生成模型取得了顯著提升。

顧名思義，生成模型生成新的、逼真的樣本，其中「逼真」通常指的是樣本在某個參考分布下具有較高的概率。

對于某些數(shù)據(jù)分布（例如自然圖像或自然語言），單個樣本所包含的信息量可能非常龐大。

為了降低生成模型的計算負(fù)擔(dān)，一種常見策略是將生成單個樣本的任務(wù)拆分為多個推理步驟。

每個步驟本身相對簡單，但當(dāng)所有步驟組合在一起時，能夠恢復(fù)完整的分布。

在自然語言處理領(lǐng)域，最典型的方法是自回歸建模（autoregressive modeling）。

自回歸語言建模經(jīng)典之作：https://www.jmlr.org/papers/v3/bengio03a.html

在此類方法中，生成一個句子（或序列）的過程被拆解為逐個生成單詞（或token），并使用已生成的單詞作為上下文，來預(yù)測下一個單詞。

自回歸模型存在一些天生的缺陷：（1）計算成本高；（2）長程依賴與連貫性（long-term dependencies and coherence）問題。

為了解決這些問題，研究者們付出了大量努力。

例如，通過強化學(xué)習(xí)（RL）進(jìn)行后訓(xùn)練，讓模型在多個自回歸步驟中學(xué)會序列推理，從而提升連貫性。

去噪擴(kuò)散模型，提出了不同的生成任務(wù)分解方式，可以解決這兩個限制。

擴(kuò)散模型的調(diào)用次數(shù)與樣本大小無關(guān)。

在圖像生成上，擴(kuò)展模型取得了成功，其中添加的高斯噪聲。

使用Stable Diffusion Ultra生成建的圖像，由Stable Diffusion 3.5提供支持

然而，比如自然語言上，擴(kuò)散方法并不如在圖像上如意。

廣義插值擴(kuò)散（GIDD）

掩碼擴(kuò)散（masked diffusion）技術(shù)雖廣泛應(yīng)用，但仍存在根本性局限。

主要問題源于其底層Markov鏈設(shè)計：一旦token被填充，便無法修改，可能導(dǎo)致錯誤累積或token不兼容，且缺乏修正機制，直接影響結(jié)果質(zhì)量。

另一個局限是，僅掩碼token貢獻(xiàn)損失信號，未掩碼token保持無噪聲狀態(tài)，減少了有效批大小。

一種有效解決方案是借鑒BERT，將掩碼機制與均勻噪聲結(jié)合。這種方法不僅能解決上述問題，還帶來額外優(yōu)勢：

1. 采樣階段，模型不僅能填充空白，還能修改已解碼token，提升靈活性和準(zhǔn)確性。
2. 訓(xùn)練任務(wù)更全面復(fù)雜，因為每個token都可能受噪聲影響，模型需具備糾錯能力，從而提高整體性能。

通過這種方式，模型學(xué)會識別「正確」與「錯誤」token后，可能發(fā)展出自我校正\自我糾錯能力。

然而，在特定理想擴(kuò)散路徑上訓(xùn)練擴(kuò)散模型時，仍面臨技術(shù)挑戰(zhàn)，需進(jìn)一步研究。

標(biāo)準(zhǔn)的訓(xùn)練目標(biāo)——擴(kuò)散證據(jù)下界（diffusion ELBO）—— 需要已知Markov狀態(tài)轉(zhuǎn)移才能推導(dǎo)出來。

但構(gòu)造具有特定性質(zhì)的Markov鏈通常是復(fù)雜的逆問題，并不容易直接求解。

研究人員將插值擴(kuò)散（interpolating diffusion）擴(kuò)展到任意（隨時間變化的）插值策略，避免了單獨求解特定的掩碼與均勻噪聲組合的逆問題，同時提升了模型設(shè)計的靈活性，

具體來說，提出了廣義插值離散擴(kuò)散（GIDD），是一類具有邊際前向轉(zhuǎn)移（marginal forward transitions）的擴(kuò)散模型，其形式如下：

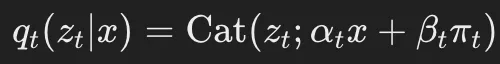
其中，π_t是一個隨時間平滑變化的概率分布。

值得注意的是，當(dāng)π_t=m時，GIDD便退化為掩碼擴(kuò)散的特例。

可以證明，在適當(dāng)選擇αt和πt的情況下，確實存在一個Markov鏈可以產(chǎn)生這些邊際分布，并推導(dǎo)其條件轉(zhuǎn)移關(guān)系以及訓(xùn)練所需的ELBO公式。

前向過程

GIDD旨在提供最大程度的靈活性，使得在任意時間點都可以對數(shù)據(jù)添加不同類型的噪聲。

其核心由兩個部分組成：

1）混合率αt：定義了隨時間變化的信噪比（signal-to-noise ratio）。

2）混合分布πt：決定了數(shù)據(jù)在某一時刻被噪聲化后的目標(biāo)分布。

研究人員將這兩個函數(shù)的組合稱為擴(kuò)散過程的「混合調(diào)度」（mixing schedule）。

定義 3.1（混合速率）：設(shè)（累積）混合速率αt和βt（其中βt=1?αt）為時間可微且遞減的函數(shù)αt:[0,1]→[0,1]，滿足初始條件α0=1（表示無混合狀態(tài)）和最終條件α1=0（表示完全混合狀態(tài)）。

這一設(shè)定決定了信噪比（SNR），即 SNR=αtβt。隨著t的增加，αt減小，表明信號成分逐漸減少，而噪聲成分逐漸增加。

定義 3.2（混合分布）：設(shè)混合分布πt是一個依賴于時間的概率向量，即時間可微函數(shù) πt:[0,1]→Δ∣V∣?1，這里 Δ∣V∣?1表示 ∣V∣維單純形。

混合分布πt描述了在任意給定時間點 tt添加到數(shù)據(jù)中的噪聲類型。因此，π1特別地代表了擴(kuò)散過程的先驗分布，它刻畫了在時間 t=1時的數(shù)據(jù)噪聲特性。

在此過程中，研究人員已經(jīng)成功構(gòu)建了一個馬爾可夫鏈，其邊緣分布按邊際前向轉(zhuǎn)移公式所述。

為了后續(xù)推導(dǎo)ELBO（證據(jù)下界），還需要定義相應(yīng)的連續(xù)時間馬爾可夫鏈（CTMC）的轉(zhuǎn)移速率，具體如下。

最終，得到了GIDD的CTMC前向速率。

反向過程

擴(kuò)散模型的標(biāo)準(zhǔn)分布pθ(zs∣zt)由以下公式給出：

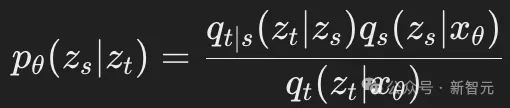
其中，qt(zt∣xθ)的簡寫形式為：

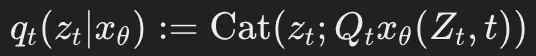
這里，xθ(Zt,t)是一個神經(jīng)網(wǎng)絡(luò)，用于預(yù)測在噪聲序列Zt條件下的x的分布。

此外，ELBO（證據(jù)下界）的推導(dǎo)涉及連續(xù)時間馬爾可夫鏈（CTMC）的反向速率。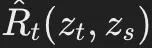

GIDD的證據(jù)下界

為了訓(xùn)練GIDD模型，需要一種可微分的方法來估計其似然函數(shù)（likelihood）。

證據(jù)下界（ELBO）正是用于此目的：通過最大化ELBO，實際上也是在最大化模型的（最壞情況下的）似然函數(shù)。

在計算ELBO時，需要用到GIDD的前向速率（forward rate）和反向速率（backward rate），這些已在前文推導(dǎo)完成。

然后，基于Campbell等人提出的ELBO形式進(jìn)行一定修改，并將GIDD的前向速率和反向速率代入，經(jīng)過化簡后得到了定理3.7。

深入分析GIDD的ELBO（證據(jù)下界），可以發(fā)現(xiàn)它實際上是在同時優(yōu)化兩個任務(wù)：

1、匹配模型與前向分布的邊際概率

2、最小化rθ(zt,x)以匹配邊際概率

有趣的是，這兩個優(yōu)化任務(wù)具有相同的全局最優(yōu)解。

這意味著，如果模型能夠完美優(yōu)化ELBO，它就能同時滿足這兩個目標(biāo)。這一特性對于理解ELBO的全局最小值及其優(yōu)化過程具有重要意義。

采樣

給定一個采樣時間表0≈t0<t1<?<tT≈1和神經(jīng)網(wǎng)絡(luò)xθ，在選定的時間網(wǎng)格上對時間進(jìn)行離散化，并采用祖先采樣（ancestral sampling）方法。

具體來說，從一個全掩碼token的序列開始，即所有ztT都設(shè)為掩碼tokenm。

然后，按照以下方式迭代采樣，其中i=T,…,1：

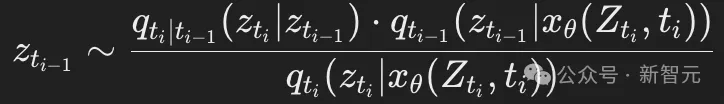
自校正步驟（Self-Correction Step）

此外，提出了一種不動點迭代方法，通過重新采樣部分token來改進(jìn)生成結(jié)果，使其更符合模型的判斷。

具體而言，將完全去噪后的樣本Z_{t_0}輸入模型，并以溫度參數(shù)τ進(jìn)行采樣。

然后，在所有與Zt0不同的采樣token中，

選擇模型置信度最高的一個token并確認(rèn)它。

這個過程會持續(xù)進(jìn)行，直到結(jié)果收斂（詳細(xì)內(nèi)容見附錄C）。

自校正算法是一種不動點迭代方法，可以應(yīng)用于任何已經(jīng)（部分）去噪的生成樣本。

其核心思想是查詢模型以識別模型認(rèn)為錯誤并應(yīng)該替換的token，并且一次只替換一個token以避免重新引入沖突token。

具體的偽代碼實現(xiàn)參見算法1。

在實際操作中，發(fā)現(xiàn)收斂往往表現(xiàn)為在兩個或多個同樣優(yōu)良狀態(tài)（就自準(zhǔn)確性而言）之間的振蕩，因此額外基于自準(zhǔn)確性實現(xiàn)了提前停止機制。

實驗表明，提前停止的耐心值設(shè)為32時效果良好。

混合策略（Mixing Schedule）

雖然GIDD可以用于掩碼擴(kuò)散，但最初提出這一廣義框架的動機是探索掩碼與均勻噪聲的結(jié)合。

為此，研究團(tuán)隊設(shè)計了一種混合策略（mixing schedule），在保持掩碼先驗分布的同時，允許在不同階段引入可調(diào)節(jié)比例的均勻噪聲。

下文中用p_u表示均勻噪聲的比例。

為了保證可解釋性，設(shè)定在數(shù)據(jù)和噪聲的中點（t=1/2）時，均勻噪聲token的期望比例達(dá)到最大值p_u。

基于這一目標(biāo)，定義了混合速率（mixing rate）和混合分布（mixing distribution）（定義3.1和3.2）。

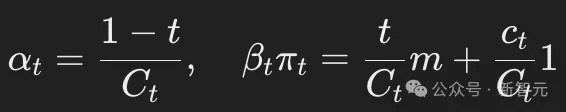
其中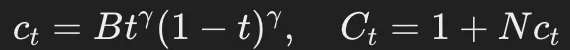：，N表示詞匯表的大小，B是一個常數(shù)，選取它的值可以保證均勻噪聲的比例達(dá)到目標(biāo)水平。

由此，得到邊際前向分布（marginal forward distribution）：

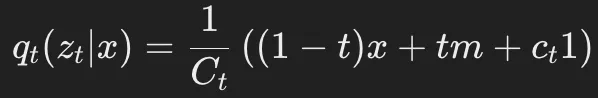
為了在t=1/2處使均勻噪聲比例達(dá)到p_u，需要設(shè)定：。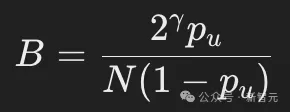

GIDD的ELBO計算涉及額外的常數(shù)和因子，需要推導(dǎo)相應(yīng)的時間導(dǎo)數(shù)。

值得注意的是，當(dāng)p_u=0.0時，GIDD退化回掩碼擴(kuò)散（masked diffusion）。

在的實驗中，設(shè)定γ=1，但本節(jié)引入的超參數(shù)仍有許多其他可能的選擇。

訓(xùn)練目標(biāo)

在開始實驗之前，需要解決最后一個關(guān)鍵問題，這一改進(jìn)將帶來顯著的性能提升。

仔細(xì)分析擴(kuò)散證據(jù)下界（ELBO）的權(quán)重wt(zt,x)后，發(fā)現(xiàn)當(dāng)t→0或t→1時，權(quán)重的變化非常極端。

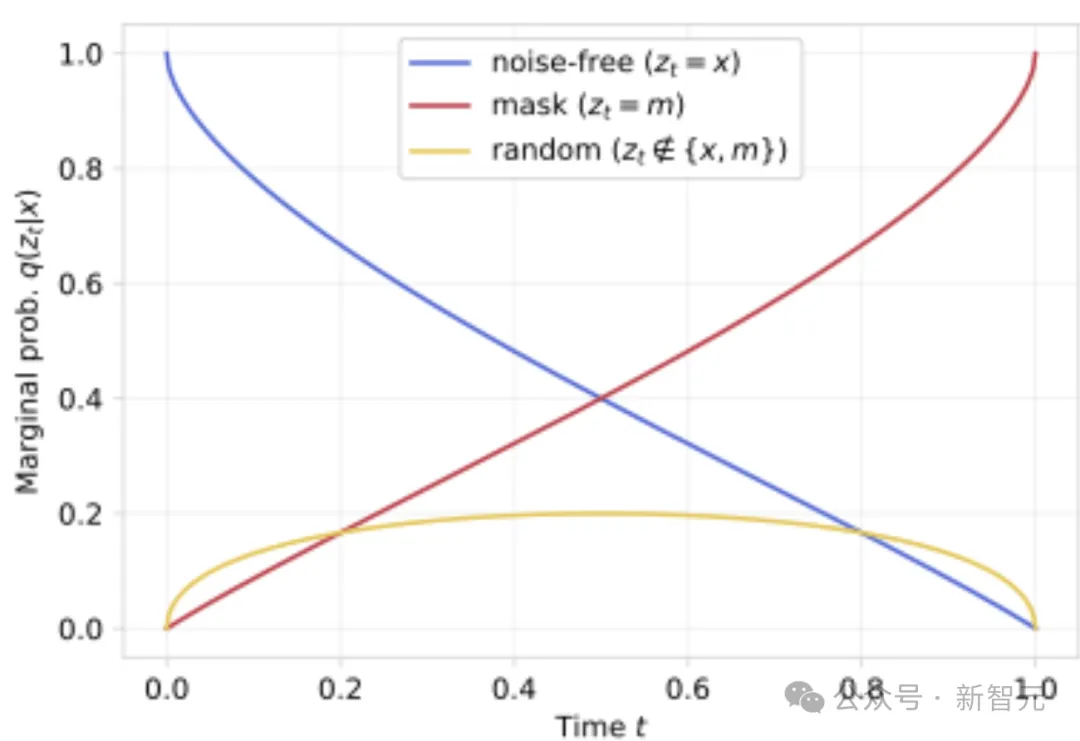
考慮以下三種可能情況：（1）z_t=x（未被噪聲污染的token）；（2）z_t=m（掩碼token）；（3）zt?{x,m}（其他隨機噪聲token）

繪制w_t(z_t,x)隨時間的變化曲線后（見圖2），可以觀察到在極低或極高噪聲水平下，權(quán)重呈指數(shù)級增長。

這種現(xiàn)象可能會帶來問題：

• 當(dāng)噪聲較低時，去噪任務(wù)變得過于簡單，模型幾乎不需要學(xué)習(xí)。
• 當(dāng)噪聲較高時，去噪任務(wù)變得幾乎不可能，模型也無法從中獲得有效的訓(xùn)練信號。
• 這兩種極端樣本的權(quán)重過高，可能會淹沒批次中的其他訓(xùn)練樣本，從而影響整體訓(xùn)練效果。

解決方案：權(quán)重裁剪（Weight Clamping）

為了解決這個問題，提出了兩種權(quán)重調(diào)整方案，以減少極端樣本的影響，并強調(diào)中等噪聲水平的樣本，因為這些樣本提供了最有價值的訓(xùn)練信號。

最簡單直接的方法是對權(quán)重設(shè)置一個最大值w_{max}，即：

根據(jù)初步實驗，發(fā)現(xiàn)設(shè)定 wmax?=1效果最佳，因此這一設(shè)定將在后續(xù)實驗中被采用。

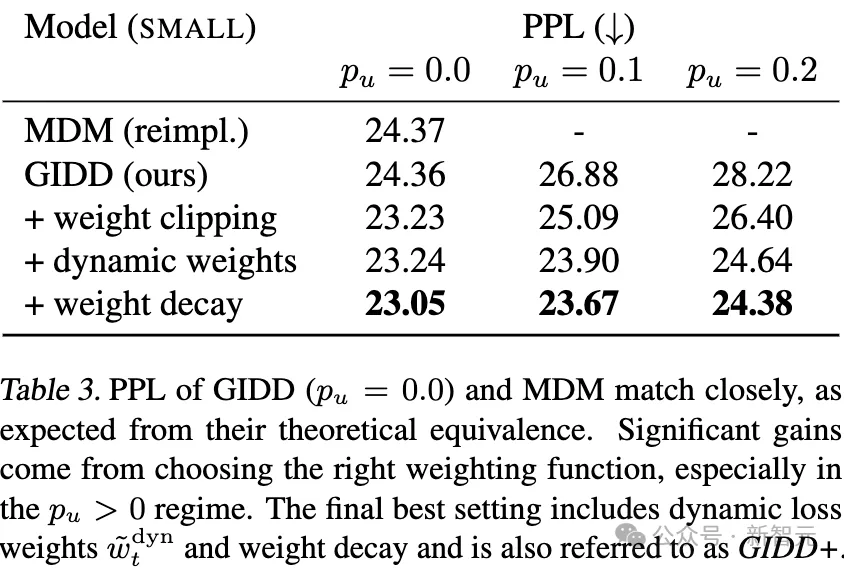
表3：GIDD（p_u = 0.0）和MDM的困惑度（PPL）非常接近，這與它們的理論等價性一致。

顯著的效果提升來自于選擇正確的權(quán)重函數(shù)，尤其是在p_u > 0的情況下。

最終的最佳設(shè)置包括動態(tài)損失權(quán)重和權(quán)重衰減，該設(shè)置也被稱為 GIDD+。

上述權(quán)重裁剪（clamping）方法主要影響掩碼token和均勻噪聲token的權(quán)重。

然而，一個更系統(tǒng)的方法是：在保持最大損失權(quán)重恒定的同時，仍然保留掩碼token、均勻噪聲token和無噪聲token之間的相對權(quán)重關(guān)系。

動態(tài)權(quán)重調(diào)整（Dynamic Weighting）

提出了一種動態(tài)加權(quán)函數(shù)（dynamic weighting function），其定義如下：

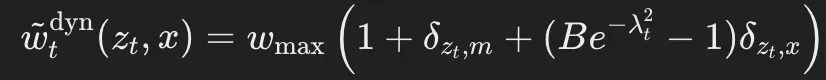
其中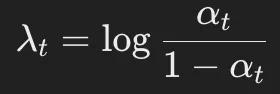，表示對數(shù)信噪比（log-SNR）。

該方法的相對權(quán)重關(guān)系（掩碼token/均勻噪聲token/無噪聲token=2/1/Be^{-λ_t^2}）是通過實驗經(jīng)驗確定的。

需要注意的是，這種ELBO重加權(quán)方法等效于從一個非均勻分布中采樣t。

自我糾正（Self-Correction）

目前為止，觀察到僅使用掩碼訓(xùn)練的模型往往優(yōu)于結(jié)合均勻噪聲的模型，但尚未討論引入均勻噪聲的核心動機：讓模型學(xué)會區(qū)分「正確」與「錯誤」token，希望它能夠具備自我糾正能力。

為了評估生成樣本的質(zhì)量，采用生成困惑度（generative perplexity,PPL）這一指標(biāo)。

具體而言，PPL計算的是生成樣本在更強大模型下的似然值，在的實驗中，使用Gemma 2 9B作為評估模型。

更高的似然值通常被認(rèn)為對應(yīng)于更高質(zhì)量的樣本。

雖然PPL作為指標(biāo)存在諸多局限性，但它在文獻(xiàn)中被廣泛采用，并且在相對比較不同模型的質(zhì)量時依然具有參考價值。

除了PPL，還評估了模型的自我準(zhǔn)確率（Self-Accuracy）。

即模型在生成過程中，對其認(rèn)為「正確」的token（即在整個序列中賦予某個token最高概率）所占的比例。

值得注意的是，在進(jìn)行自我糾正之前，訓(xùn)練時加入均勻噪聲的模型樣本質(zhì)量已經(jīng)更高。

尤其是在低計算量推理（low inference-compute）設(shè)置下，相較于僅使用掩碼的模型，其生成困惑度（generative PPL）提升尤為顯著。

例如，在32步推理時：

• GIDD+（SMALL;p_u=0.1）的PPL為387;
• 僅掩碼模型（p_u=0.0）的PPL為904;
• MDM（masked diffusion model）的PPL更高，達(dá)到1302。

這表明，訓(xùn)練時加入均勻噪聲可以穩(wěn)定生成過程，特別是在模型將自身生成的輸出作為輸入時，使得樣本質(zhì)量更高——即使其驗證困惑度（validation PPL）略有下降。

這一發(fā)現(xiàn)引發(fā)了一個重要問題：自我糾正的效果是否只是因為額外的去噪迭代次數(shù)？

換句話說，模型在去噪過程中可能已經(jīng)在執(zhí)行一定程度的自我糾正，因此自我糾正步驟帶來的提升，是否僅僅是因為額外的計算次數(shù)？

從實驗來看，雖然增加去噪步驟確實會單調(diào)提升樣本質(zhì)量，但這種提升最終會趨于飽和（對于BASE模型，PPL約停留在200）。

然而，當(dāng)引入自我糾正機制后，PPL可以進(jìn)一步降低到100以下，這表明自我糾正帶來的改進(jìn)并非僅僅是更多去噪迭代的結(jié)果，而是一種額外的、非平凡（non-trivial）的提升。

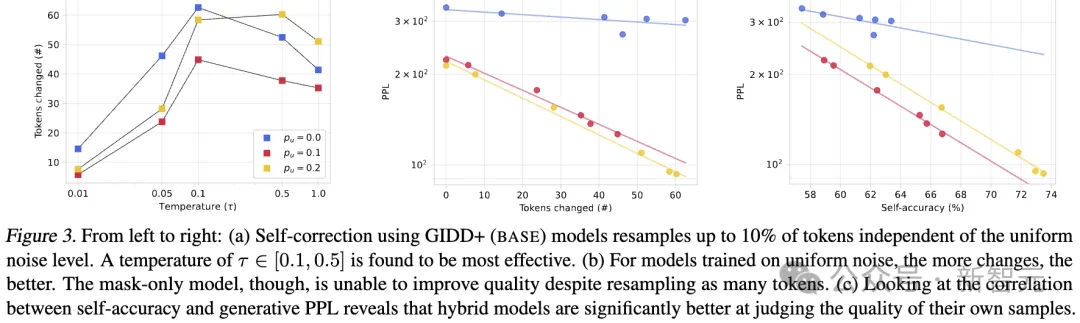
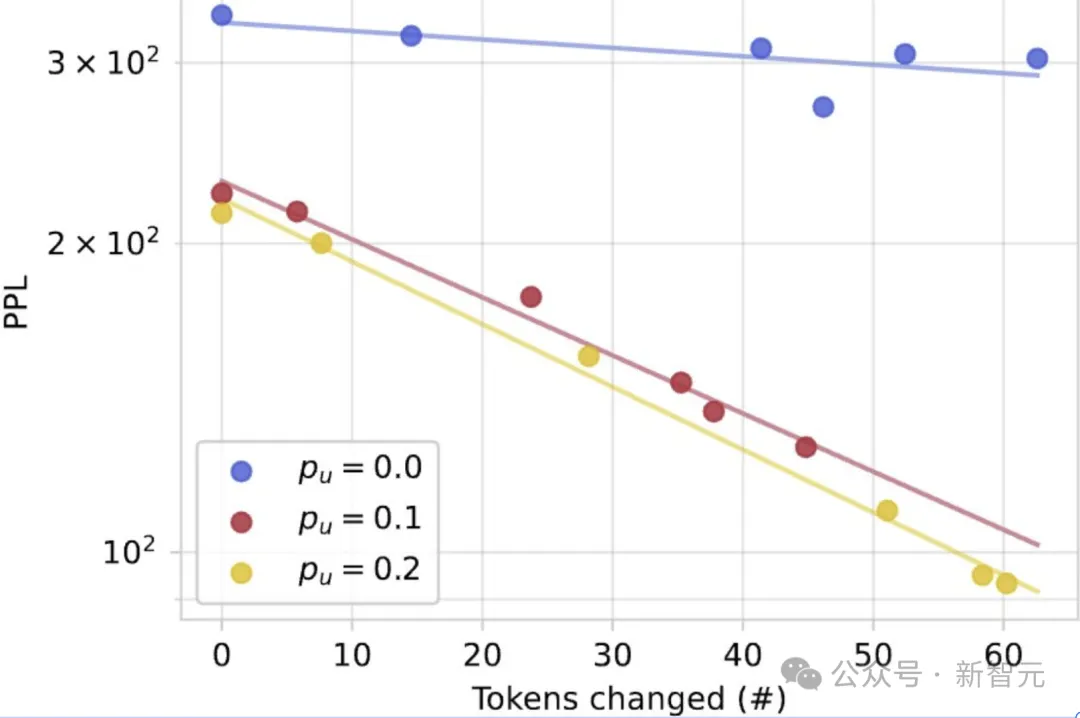
圖3|從左到右（a）不同溫度下token數(shù)變化；（b）token變化數(shù)與PPL的關(guān)系；（c）自我準(zhǔn)確性與生成困惑度之間的相關(guān)性.

具體結(jié)果如下：

(a) 使用 GIDD+ (BASE) 模型進(jìn)行自我糾正時，可以重新采樣最多10%的token，這一過程與均勻噪聲水平無關(guān)。研究發(fā)現(xiàn)，溫度參數(shù)τ取值在 [0.1, 0.5] 之間時效果最佳。

(b) 對于在均勻噪聲上訓(xùn)練的模型來說，采樣的token數(shù)量越多，效果越好。然而，僅使用掩碼（mask-only）的模型即使重新采樣了同樣數(shù)量的token，也無法提升質(zhì)量。

(c) 通過分析自我準(zhǔn)確性（self-accuracy）與生成困惑度（generative PPL）之間的相關(guān)性，發(fā)現(xiàn)混合模型在評估自身生成樣本的質(zhì)量方面明顯更具優(yōu)勢。

下游人物性能

在一系列基準(zhǔn)測試中評估了模型的語言理解能力。基于混合噪聲設(shè)置p_u > 0的更高難度，預(yù)計這些模型不會超過僅使用掩碼噪聲p_u = 0的情況，實驗結(jié)果也證實了這一點。

因此，研究人員將重點放在比較最佳的 SMALL GIDD+ 模型與MDM以及自回歸基線模型（即 GPT2（和重新訓(xùn)練的 Llama上。

作為參考，還納入了兩個 1.1B 參數(shù)模型，一個是自回歸模型，另一個是掩碼擴(kuò)散模型。

基準(zhǔn)測試包括ARC-e和ARC-c、BoolQ、Hellaswag、PIQA、OpenBookQA以及WinoGrande。

實驗發(fā)現(xiàn)，平均準(zhǔn)確率與驗證困惑度（PPL）通常有很好的相關(guān)性（見表4）。

在擴(kuò)散模型中，表現(xiàn)最好的是僅訓(xùn)練了131B token的GIDD+（p_u=0.0），超過了訓(xùn)練時間兩倍的模型。

這可能是由于模型在訓(xùn)練數(shù)據(jù)中的虛假模式上過擬合，雖然驗證損失仍然下降，但并未轉(zhuǎn)化為下游任務(wù)的性能提升。

值得注意的是，最佳擴(kuò)散模型GIDD+的表現(xiàn)優(yōu)于自回歸模型 GPT2，盡管訓(xùn)練數(shù)據(jù)的差異使得公平比較有些困難。實際上，最佳自回歸模型 Llama（重新訓(xùn)練版本） 仍然在總體上表現(xiàn)最佳，但平均差距不到一個百分點。

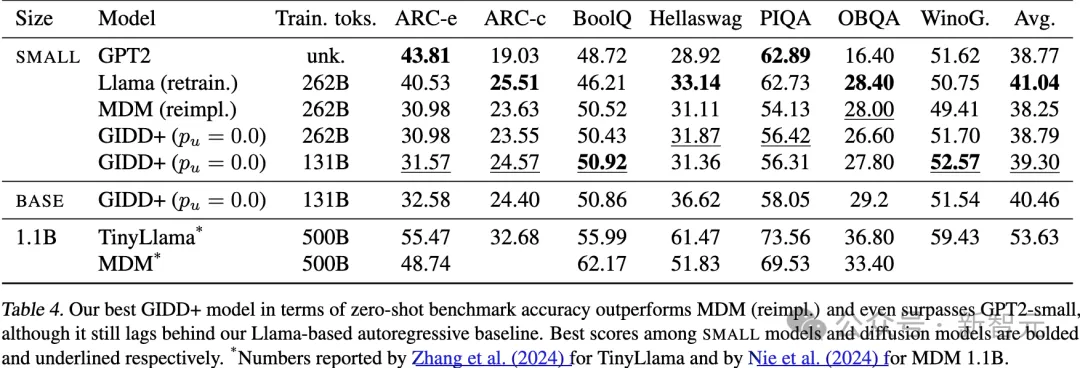
表4：不同模型的零樣本(Zero-shot)基準(zhǔn)準(zhǔn)確率。在小型模型和擴(kuò)散模型中分別用粗體和下劃線_標(biāo)出了最佳分?jǐn)?shù)。

對于使用均勻噪聲訓(xùn)練的 GIDD 模型，其趨勢與驗證困惑度一致，更多的均勻噪聲通常會降低準(zhǔn)確率。

下表5中列出了三種規(guī)模（TINY、SMALL、BASE）和所有均勻噪聲水 0.0, 0.1, 0.2的GIDD+模型的基準(zhǔn)測試準(zhǔn)確率。

無論均勻噪聲水平如何，模型的性能都隨著規(guī)模的增加而持續(xù)提升。然而，使用均勻噪聲訓(xùn)練的模型，在性能上略微但持續(xù)落后于僅使用掩碼噪聲的模型。

然而，隨著模型規(guī)模的增加，性能持續(xù)提升，初步跡象表明，隨著規(guī)模的擴(kuò)大，差距可能會縮小。

直觀地說，均勻噪聲讓訓(xùn)練任務(wù)變得更難：模型不能再理所當(dāng)然地認(rèn)為每個未掩碼的token都是正確的，而是必須考慮上下文中的每個token，并在必要時將其替換為正確的token。

這種直觀的解釋表明，觀察到的性能差異可能是由于模型容量不足，在這種情況下，預(yù)計更大的模型受均勻噪聲的影響會更小。

為了驗證這一假設(shè)，在保持訓(xùn)練時長不變的情況下擴(kuò)展了參數(shù)數(shù)量，并訓(xùn)練了不同規(guī)模（TINY、SMALL 和 BASE）的模型，分別在不同的均勻噪聲水平0.0, 0.1, 0.2下進(jìn)行訓(xùn)練。

然后，通過指數(shù)擬合繪制了計算效率前沿，反映帕累托最優(yōu)的驗證 ELBO（見圖 4）。

One More Thing：只是小規(guī)模實驗

由于資源限制，實驗設(shè)置有一定的局限性：

每個噪聲水平的樣本量僅限于三種不同的計算預(yù)算，其中最大的計算預(yù)算仍然相對較小，僅為3.3*10^{20} FLOPs。

作為參考，現(xiàn)代大語言模型的許多標(biāo)志性能力通常需要達(dá)到 10^{22} FLOPs 左右才會開始顯現(xiàn)，這仍然比我們最大的計算預(yù)算高出兩個數(shù)量級。

盡管如此，確實觀察到了一個一致的趨勢，即隨著計算資源的增加，較高水平的均勻噪聲表現(xiàn)更好，盡管這一趨勢的幅度較小。

在僅使用掩碼噪聲的設(shè)置p_u = 0.0中，擴(kuò)展指數(shù)為-0.0586，而加入均勻噪聲后，p_u = 0.1和p_u = 0.2 的擴(kuò)展指數(shù)分別提高到-0.0589和-0.0621。

外推這一趨勢預(yù)測，p_u = 0.2的設(shè)置將在10^{21}FLOPs 左右超過 p_u = 0.0，這一計算預(yù)算在中到大規(guī)模的訓(xùn)練中通常可以達(dá)到。

然而，必須強調(diào)的是，這次的實驗設(shè)置的局限性使得這種預(yù)測的可靠性較低。

盡管如此，觀察到的擴(kuò)展行為是令人鼓舞的，值得進(jìn)一步研究。