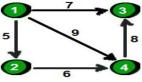
你了解鄰接表和鄰接矩陣嗎？圖的世界從這里開始！
作者：Ss肥魚
圖的表示是學習圖論的第一步，選對了數據結構，算法才能高效執行。無論是遍歷、最短路徑，還是拓撲排序，理解鄰接表和鄰接矩陣的差異都是基礎能力。?
在算法和數據結構的學習中，圖 是一個比樹更為復雜、但也更貼近實際問題的結構。比如社交網絡、電網布局、地圖導航系統、任務調度等，底層都依賴于圖的結構來建模。
而在正式編寫圖的算法之前，我們必須先搞懂：如何用代碼來表示圖？
一、什么是圖？
圖（Graph）是一種由**節點（頂點）和邊（連接）**組成的結構。每個節點可以和多個節點連接。
圖可以是：
- 有向圖（邊有方向）
- 無向圖（邊沒有方向）
- 帶權圖（邊上有權重，比如距離、成本）
二、圖的兩種常見表示法
在實際應用中，我們常用以下兩種方式來表示圖：
1. 鄰接矩陣（Adjacency Matrix）
鄰接矩陣使用一個 N x N 的二維數組來表示頂點之間的連接關系。
# 頂點列表：0, 1, 2
# 邊：0->1，1->2
graph = [
[0, 1, 0], # 0 到 1 有邊
[0, 0, 1], # 1 到 2 有邊
[0, 0, 0] # 2 沒有出邊
]每個 graph[i][j] = 1 表示節點 i 指向節點 j。
優缺點：
優點 | 缺點 |
查找兩點是否相鄰非常快（O(1)） | 空間浪費嚴重，尤其是稀疏圖（O(n2)） |
2. 鄰接表（Adjacency List）
鄰接表使用一個字典（或列表）存儲每個節點的相鄰節點列表，更節省空間。
graph = {
0: [1],
1: [2],
2: []
}每個 key 表示一個節點，對應的 value 是它指向的節點集合。
優缺點：
優點 | 缺點 |
更節省空間，適合稀疏圖（O(n + m)） | 查找相鄰關系較慢（O(k)） |
三、使用類封裝圖結構（推薦做法）
在大型項目或算法中，封裝為類能更方便維護：
class Graph:
def __init__(self, num_nodes):
self.num_nodes = num_nodes
self.adj_list = {i: [] for i in range(num_nodes)}
def add_edge(self, src, dest):
self.adj_list[src].append(dest)
def __str__(self):
return "\n".join(f"{k} -> {v}" for k, v in self.adj_list.items())
# 示例：
g = Graph(3)
g.add_edge(0, 1)
g.add_edge(1, 2)
print(g)輸出結果：
0 -> [1]
1 -> [2]
2 -> []四、選用哪種表示方式？
情況 | 推薦方式 |
稠密圖（邊接近 n2） | 鄰接矩陣 |
稀疏圖（邊遠少于 n2） | 鄰接表 |
頻繁查是否存在一條邊 | 鄰接矩陣 |
節點較多但連接較少（常見場景） | 鄰接表 |
五、小結
圖的表示是學習圖論的第一步，選對了數據結構，算法才能高效執行。無論是遍歷、最短路徑，還是拓撲排序，理解鄰接表和鄰接矩陣的差異都是基礎能力。
責任編輯：趙寧寧
來源：
Ssoul肥魚
