12.1萬(wàn)道IMO級(jí)難度數(shù)學(xué)“特訓(xùn)題”，讓AI學(xué)會(huì)像人類(lèi)一樣推導(dǎo)數(shù)學(xué)證明！

“特訓(xùn)”過(guò)后，模型定理證明性能大漲，7B模型性能比肩或超越現(xiàn)有的開(kāi)源模型和Claude3.7等商業(yè)模型。

“特訓(xùn)題”為DeepTheorem，是首個(gè)基于自然語(yǔ)言的數(shù)學(xué)定理證明框架與數(shù)據(jù)集，由騰訊AI Lab與上海交大團(tuán)隊(duì)聯(lián)合推出。

團(tuán)隊(duì)表示，定理證明是數(shù)學(xué)前沿的重要組成部分，但當(dāng)前大語(yǔ)言模型（LLM）在數(shù)學(xué)推理，特別是通過(guò)強(qiáng)化學(xué)習(xí)（RL）進(jìn)行訓(xùn)練時(shí)，往往需要可以自動(dòng)驗(yàn)證的答案，導(dǎo)致大模型無(wú)法像數(shù)學(xué)家那樣通過(guò)自然語(yǔ)言進(jìn)行定理證明。

而當(dāng)前研究者通常通過(guò)使用大模型生成Lean、Coq、Isabelle等形式語(yǔ)言，配合外部定理證明引擎進(jìn)行定理證明，無(wú)法充分利用LLM在自然語(yǔ)言預(yù)訓(xùn)練過(guò)程中獲得的能力。

為解決這一問(wèn)題，DeepTheorem框架橫空出世，包含了從數(shù)據(jù)、訓(xùn)練、測(cè)試到評(píng)估的完整四部分：

• 121K大規(guī)模、高難度、嚴(yán)格去污染的自然語(yǔ)言定理與o3-mini生成的配套證明過(guò)程
• 首個(gè)使用強(qiáng)化學(xué)習(xí)進(jìn)行數(shù)學(xué)定理證明的方法
• 分別基于FIMO、HMMT、PutnamBench構(gòu)建的三個(gè)自然語(yǔ)言定理證明測(cè)試集
• 涵蓋結(jié)果監(jiān)督與過(guò)程監(jiān)督的全面評(píng)價(jià)指標(biāo)

如下圖（a）所示，DeepTheorem數(shù)據(jù)在規(guī)模和難度上均顯著超越目前已有的公開(kāi)定理數(shù)據(jù)集。

圖（b）展示經(jīng)過(guò)強(qiáng)化學(xué)習(xí)訓(xùn)練的DeepTheorem-7B模型性能，比肩或超越現(xiàn)有的開(kāi)源模型和商業(yè)模型（Gemini2.0-flash， Qwen2.5-72B-Instruct， Claude3.7等），僅次于o1、o3以及Gemini2.5-pro強(qiáng)推理模型。

DeepTheorem-121K

1、規(guī)模與難度：專(zhuān)為“極限挑戰(zhàn)”而生

DeepTheorem訓(xùn)練集的顯著特點(diǎn)是其大規(guī)模與高難度。其包含121K精心構(gòu)造的數(shù)學(xué)定理，難度等級(jí)為5-9級(jí)，規(guī)模顯著大于現(xiàn)有數(shù)學(xué)定理數(shù)據(jù)且難度更高，與FIMO等國(guó)際數(shù)學(xué)奧賽級(jí)別的測(cè)試集難度分布相似。

2、嚴(yán)格去污染：確保評(píng)估“純凈”

DeepTheorem訓(xùn)練集的構(gòu)建過(guò)程堪稱(chēng)“匠心獨(dú)運(yùn)”，通過(guò)一個(gè)細(xì)致的五階段流程構(gòu)造：

來(lái)源分析與收集：分析現(xiàn)有數(shù)據(jù)來(lái)源，選擇難題比例高的數(shù)據(jù)源。

數(shù)據(jù)去污染：使用嵌入相似性搜索和LLM-Judge來(lái)識(shí)別并消除與MATH、AIME、GPQA等14個(gè)通用數(shù)學(xué)和STEM基準(zhǔn)以及miniF2F、PutnamBench、FIMO等四個(gè)數(shù)學(xué)定理證明基準(zhǔn)的重疊，確保評(píng)估的完整性并防止數(shù)據(jù)泄露。

證明生成與質(zhì)量控制：使用o3-mini生成定理證明過(guò)程，并使用GPT-4o對(duì)定理完整性進(jìn)行評(píng)估，保留定理與證明過(guò)程完整的樣本。

難度過(guò)濾：使用GPT-4o對(duì)定理進(jìn)行難度評(píng)估，保留難度等級(jí)5或更高的定理。

單命題過(guò)濾：根據(jù)定理中的子命題個(gè)數(shù)進(jìn)行篩選，保留僅含一個(gè)自命題的定理。

3、獨(dú)特結(jié)構(gòu)：兼顧SFT與RL

DeepTheorem訓(xùn)練集中的每條數(shù)據(jù)都包含豐富的信息，支持多種數(shù)學(xué)推理研究和應(yīng)用：

• 問(wèn)題：核心的數(shù)學(xué)定理陳述。
• 最終答案：定理的真值（真或假），這對(duì)于在可驗(yàn)證獎(jiǎng)勵(lì)強(qiáng)化學(xué)習(xí)（RLVR）中基于規(guī)則的獎(jiǎng)勵(lì)函數(shù)至關(guān)重要，是自動(dòng)化評(píng)估和反饋的基礎(chǔ)。
• 難度：數(shù)值難度標(biāo)注，支持難度感知訓(xùn)練。
• 主題：分層主題分類(lèi)，涵蓋從初等代數(shù)到抽象代數(shù)、微積分的廣泛數(shù)學(xué)主題。
• o3-mini證明過(guò)程：由o3-mini模型生成的證明過(guò)程，對(duì)于監(jiān)督微調(diào)和模型蒸餾等多種訓(xùn)練范式都具有巨大價(jià)值。

將RL-Zero引入數(shù)學(xué)定理證明

1、數(shù)據(jù)增強(qiáng)：定理可以被證明，也可以被證偽

為將可驗(yàn)證獎(jiǎng)勵(lì)強(qiáng)化學(xué)習(xí)（RLVR）引入自然語(yǔ)言數(shù)學(xué)定理證明，DeepTheorem通過(guò)自動(dòng)化的方法來(lái)對(duì)每個(gè)原始定理進(jìn)行擴(kuò)展，衍生出多個(gè)可被證明或證偽的變體。

以定理“x>1”為例，若該定理成立，則變體一“x>0”也一定成立，而變體二“x<1”則一定不成立。通過(guò)這種方式，DeepTheorem僅基于定理本身（而不需要接觸證明過(guò)程）使用大模型對(duì)訓(xùn)練集中的所有定理進(jìn)行擴(kuò)展，獲得242K定理及變體。

2、二值獎(jiǎng)勵(lì)激發(fā)定理證明能力

在獲得定理變體后，DeepTheorem使用基于GRPO的RLVR進(jìn)行定理證明訓(xùn)練。對(duì)于訓(xùn)練集中的每一個(gè)定理，模型的任務(wù)是將其證明或證偽，并在最終答案中給出判斷（證明或證偽）。

基于規(guī)則的獎(jiǎng)勵(lì)函數(shù)根據(jù)模型最終答案進(jìn)行打分，若答案正確則得一分，若無(wú)法提取答案或答案錯(cuò)誤則得0分。

DeepTheorem評(píng)估框架

1、DeepTheorem測(cè)試集

在經(jīng)過(guò)對(duì)問(wèn)題難度、污染程度、數(shù)據(jù)可用性等多方面因素的綜合考慮后，作者們選擇了兩個(gè)現(xiàn)有的定理證明測(cè)試集FIMO與PutnamBench，并從當(dāng)前污染較少的HMMT測(cè)試集中手工篩出了定理證明相關(guān)題目，構(gòu)成三個(gè)自然語(yǔ)言定理證明測(cè)試集。

模仿對(duì)訓(xùn)練數(shù)據(jù)中的定理進(jìn)行數(shù)據(jù)增強(qiáng)的方式，DeepTheorem的作者們對(duì)這三個(gè)測(cè)試集中的每個(gè)定理手工擴(kuò)展出了多個(gè)變體，構(gòu)成最終測(cè)試集：

最終測(cè)試集中，平均每個(gè)定理包含約三個(gè)變體，三個(gè)測(cè)試集總變體數(shù)658個(gè)。

2、結(jié)果與過(guò)程評(píng)價(jià)指標(biāo)

在DeepTheorem測(cè)試集上，模型性能由兩部分評(píng)價(jià)指標(biāo)構(gòu)成：結(jié)果評(píng)價(jià)與過(guò)程評(píng)價(jià)。

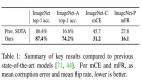
結(jié)果評(píng)價(jià)的指標(biāo)定義為：對(duì)每一個(gè)原始定理，若模型成功將其全部變體證明或證偽則得1分，否則得0分。基于此定義，我們可以對(duì)每個(gè)變體隨機(jī)賦予“證明”或“證偽”的答案獲得隨機(jī)基線。此基線在三個(gè)測(cè)試集上的性能如上表Random Acc.列所示。

過(guò)程評(píng)價(jià)使用LLM-as-Judge，由GPT-4o從邏輯正確性、完整性、最終答案正確性以及過(guò)程清晰性四個(gè)維度對(duì)證明過(guò)程進(jìn)行打分。

DeepTheorem模型性能達(dá)到SOTA

實(shí)驗(yàn)結(jié)果表明，在DeepTheorem數(shù)據(jù)集上使用RL-Zero基于Qwen2.5-7B訓(xùn)練的模型擁有同規(guī)模模型中的SOTA性能。

顯著優(yōu)于DeepSeek-Prover等參數(shù)量相近的現(xiàn)有定理證明模型以及Qwen2.5-Math-72B等更大的模型，甚至比肩Claude3.7-Sonnet等閉源模型，在所評(píng)測(cè)的18個(gè)模型中性能排名第五，僅次于o1系列、o3-mini以及Gemini 2.5 Pro。

以下為DeepTheorem-RL-7B在測(cè)試集上隨機(jī)挑選的輸出樣本。模型在證明過(guò)程中展現(xiàn)出了清晰準(zhǔn)確的邏輯性，且僅使用Latex，簡(jiǎn)潔易懂。

團(tuán)隊(duì)表示，DeepTheorem框架的發(fā)布，無(wú)疑為人工智能在數(shù)學(xué)推理領(lǐng)域的應(yīng)用開(kāi)辟了全新的思路，它不僅突破了使用形式語(yǔ)言進(jìn)行定理證明的傳統(tǒng)范式限制，更通過(guò)其大規(guī)模、高質(zhì)量的訓(xùn)練數(shù)據(jù)提升了AI在前沿?cái)?shù)學(xué)方面的卓越性能。

我們期待，在DeepTheorem的推動(dòng)下，AI能夠真正學(xué)會(huì)定理證明，從封閉的計(jì)算、簡(jiǎn)答題目走向更廣闊的數(shù)學(xué)殿堂，最終邁向更強(qiáng)大、更具通用性、認(rèn)知上更復(fù)雜的智能系統(tǒng)。

團(tuán)隊(duì)簡(jiǎn)介

本文通訊作者徐嘉豪， 騰訊AI Lab高級(jí)研究員，研究方向?yàn)橥评泶竽Ｐ停贜IPS，ACL，EMNLP等國(guó)際頂級(jí)會(huì)議上發(fā)表多篇論文。

共同通訊作者涂兆鵬，騰訊混元數(shù)字人專(zhuān)家研究員，研究方向?yàn)樯疃葘W(xué)習(xí)和大模型，在國(guó)際頂級(jí)期刊和會(huì)議上發(fā)表學(xué)術(shù)論文一百余篇，多次擔(dān)任ACL、EMNLP、ICLR等國(guó)際頂級(jí)會(huì)議領(lǐng)域主席。

共同通訊作者王瑞，上海交通大學(xué)副教授，研究方向?yàn)橛?jì)算語(yǔ)言學(xué)。

第一作者為上海交通大學(xué)博士生張子殷。

論文地址：https://arxiv.org/abs/2505.23754

數(shù)據(jù)地址：https://huggingface.co/datasets/Jiahao004/DeepTheorem

代碼地址：https://github.com/Jiahao004/DeepTheorem