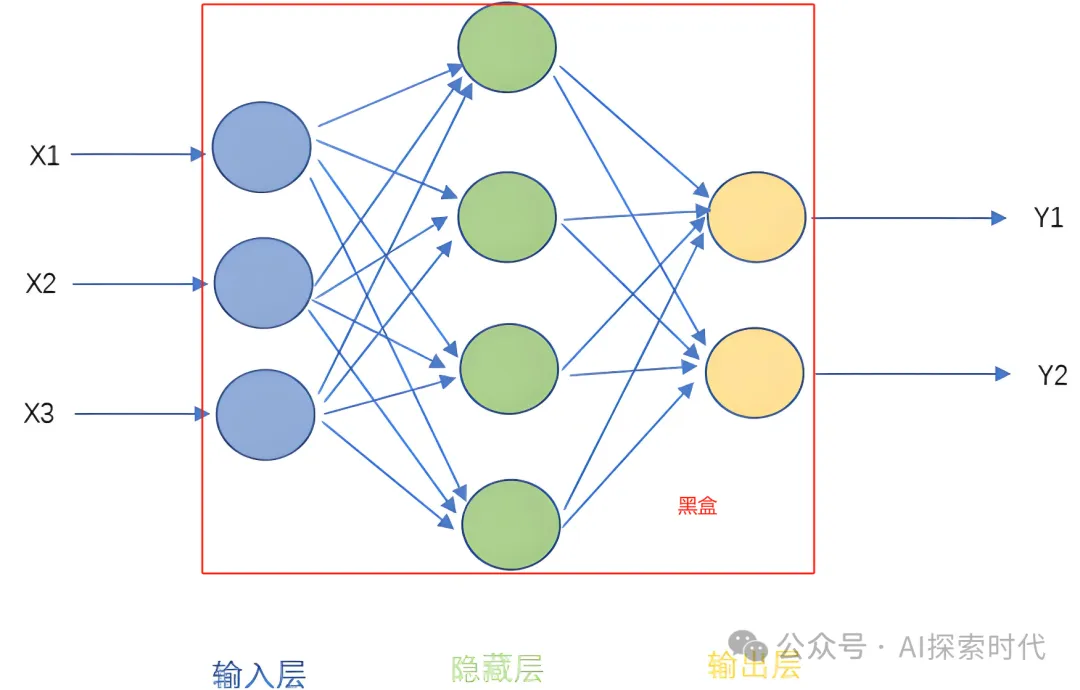
“ 神經網絡就是一個具有輸入和輸出的黑盒”

神經網絡模型就是模仿人類大腦神經元傳遞的過程，從使用者的角度來說，神經網絡就是一個具有輸入和輸出的黑盒模型。

簡化模型如下圖：

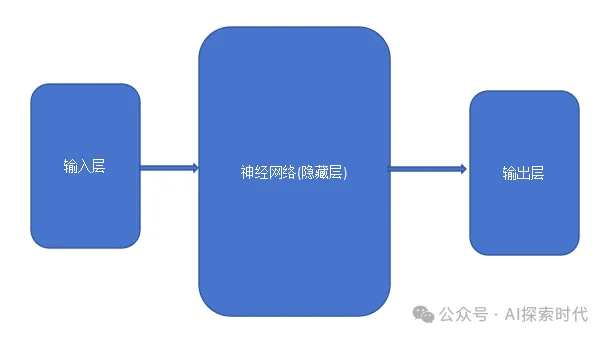
只需要設定特定的輸入和輸出格式，隱藏層可以根據不同的任務需求進行實現。

01、神經網絡模型

神經網絡主要由神經元構成，然后會根據任務復雜度，設計一個到多個網絡層，網絡層數越多，處理的問題越復雜。

如下圖所示，就是一個簡單的神經網絡模型圖，具有輸入層，輸出層和隱藏層，隱藏層并不一定就一層，也可能由多層網絡組成，每一層又由多個神經元組成。

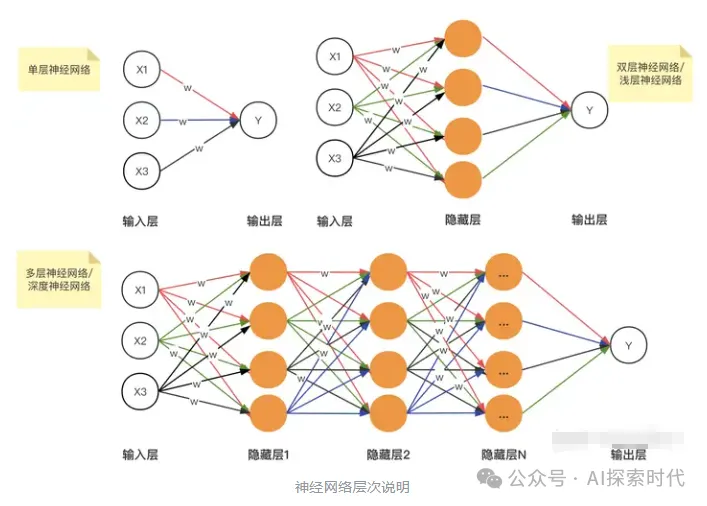
神經網絡可以分為：輸入層、隱藏層、輸出層，其中隱藏層數量決定模型網絡復雜度

輸入層是神經網絡的第一層，其作用是接收輸入數據，并將其傳遞到下一層。

隱藏層是位于輸入層和輸出層之間的一層或多層。其作用是將輸入數據轉換為更高層次的特征表示，神經網絡的核心處理模塊就在隱藏層。

輸出層是神經網絡的最后一層，其作用是將神經網絡對輸入數據的處理結果輸出。

輸入層

輸入層是神經網絡的第一層，也是唯一與外界交互的一層，它的作用就是從外界獲取數據，并輸入到它的下一層，它的下一層可以是隱藏層也可以是輸出層。

在神經網絡中，輸入層是需要從外部獲取數據，而不是由訓練得到的數據；因此，在神經網絡的設計中，輸入層需要根據不同的數據特征進行適當的調整和泛化。

比如在圖像處理的神經網絡中，需要考慮圖片的尺寸，顏色空間等；而在自然語言處理(NLP)中，又需要考慮分詞，詞匯表等。

輸入層的神經元數量一般由輸入的數據特征來確定，比如圖片處理任務中，每一個像素點就是一個神經元。

因此，輸入層作為神經網絡的第一層，它的作用就是把輸入數據(文字，圖片，視頻等一切數據)，轉化為神經網絡可以處理的格式。

所以，在設計輸入層時，要考慮輸入數據的格式及各種預處理，并且要具有適當的泛化能力，比如某一天需要增加某些數據格式等，并且根據不同的任務類型可以進行適當的調整。

輸入層就類似于一個適配器或轉化器，把人類的數據格式適配到神經網絡中。

隱藏層

隱藏層是位于輸入層與輸出層之間的一層或多層，隱藏層是神經網絡的核心處理模塊，它可以把輸入層的數據轉換為更高層次的特征表示；并且，每個隱藏層的神經元數量和連接方式都不相同，這取決于具體的神經網絡架構。

比如，卷積網絡的隱藏層主要有卷積層，池化層和線性層。

隱藏層的好壞和架構，直接決定著這個神經網絡的功能與性能，以及訓練的成本等問題。隱藏層的神經元越多，網絡層數越多，那么它的表示能力越強，處理的問題也就更復雜。

因此，隱藏層的設計也需要根據不同的任務類型進行適當的泛化和調整，并且設計一個良好的隱藏層也需要豐富的理論基礎以及實踐經驗。

隨著神經網絡的發展，隱藏層會變得越來越多，越來越復雜；也可能會出現更加新穎和強大的架構。

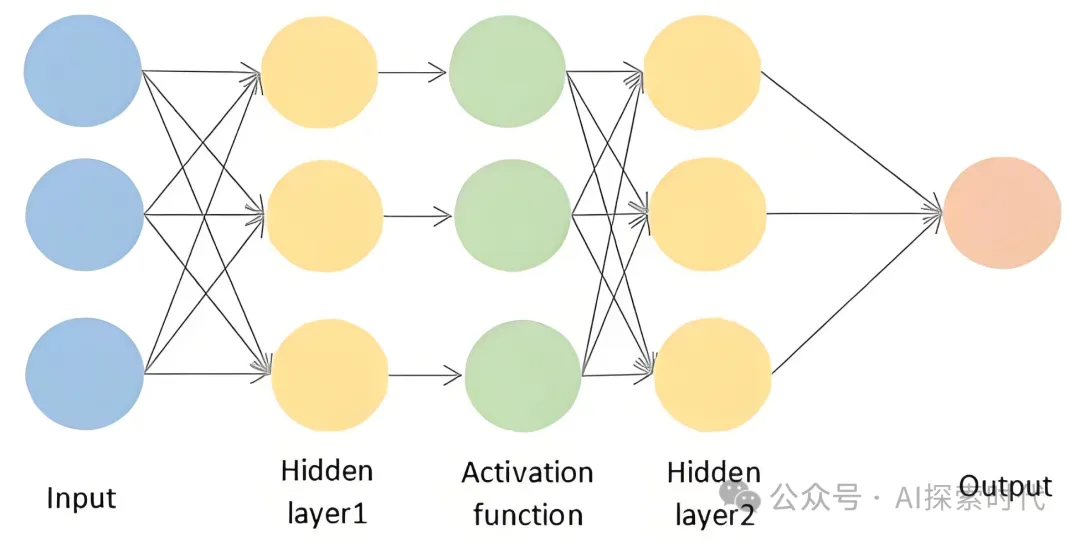
輸出層

輸出層是神經網絡模型中的最后一層，其作用是輸出神經網絡的處理結果，嚴格來說是隱藏層的處理結果；輸出層一般只有一個神經元，其值就是神經網絡的處理結果。

在訓練的過程中，輸出層的輸出結果需要使用損失函數計算損失差，而訓練的目的就是不斷的減少損失差。

輸出層同樣也需要根據不同的任務類型，進行適當的泛化和調整設計，這樣才能滿足更加復雜的輸出任務。

總結

根據不同的任務，神經網絡也分為不同的類型，比如分類任務，文本處理任務，圖片處理任務等。

根據不同的網絡架構也有不同的實現方式，比如全鏈接層就需要所有神經元參與計算。

在由多層網絡組成的隱藏層中，每一層的輸入都是上層的輸出，每一層的輸出就是下一層的輸入。

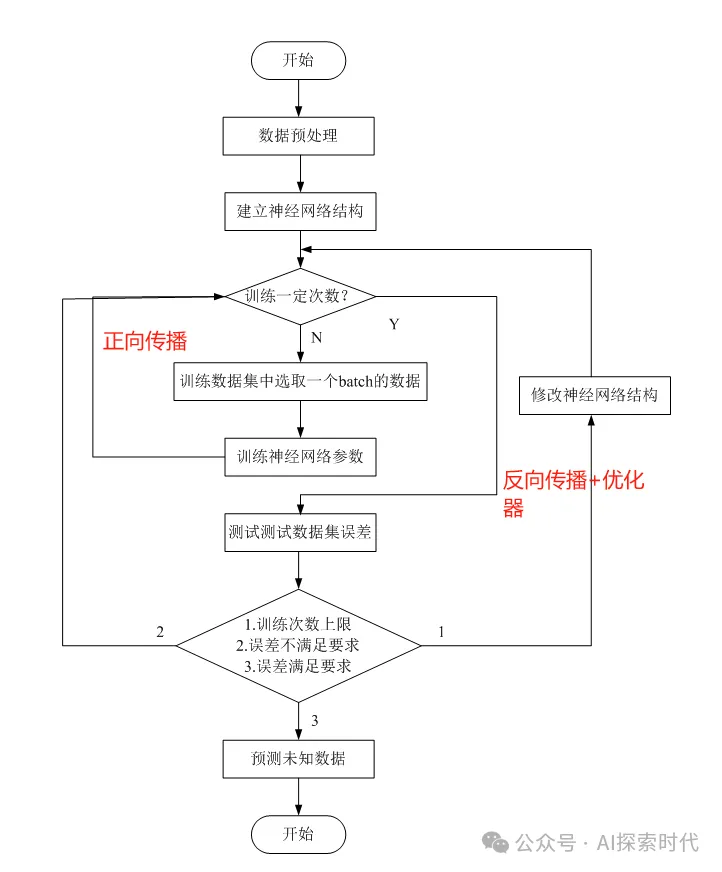
簡單來說，神經網絡就由其三大組件(輸入層，隱藏層和輸出層)組成，每一層根據不同的任務都會有不同的實現，重要的就是其泛化和擴展的能力。

最后，經過損失函數計算損失差，并通過反向傳播的方式，使用優化器優化網絡各層的參數，最后使模型達到最優。

02、神經元的原理

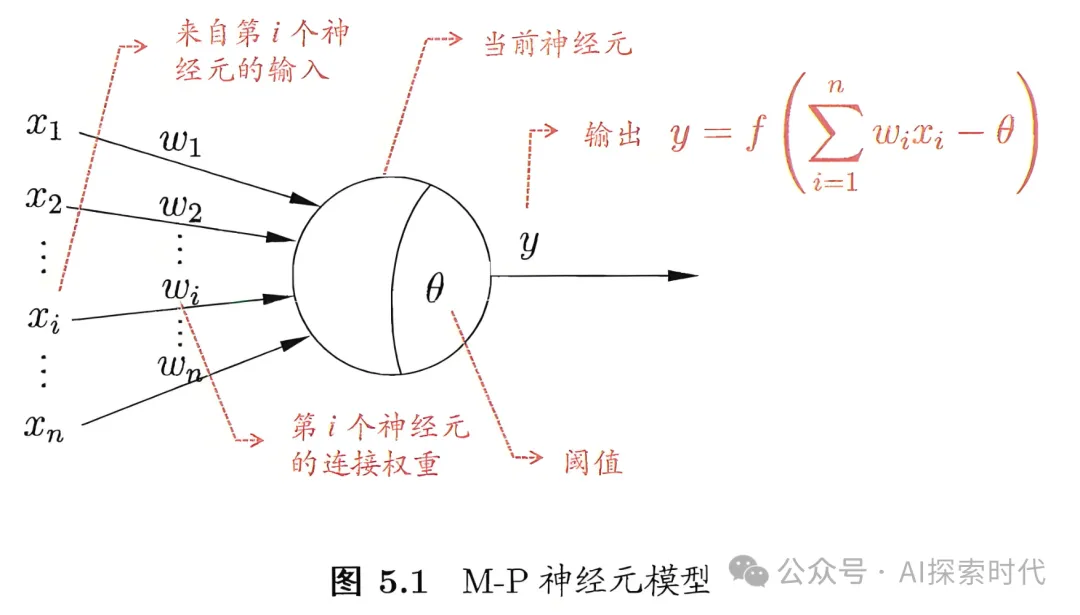
神經元是神經網絡的最小組成單位，每一層神經網絡都至少由一個神經元到多個神經元組成。

如下圖所示就是一個神經元的計算模型圖：

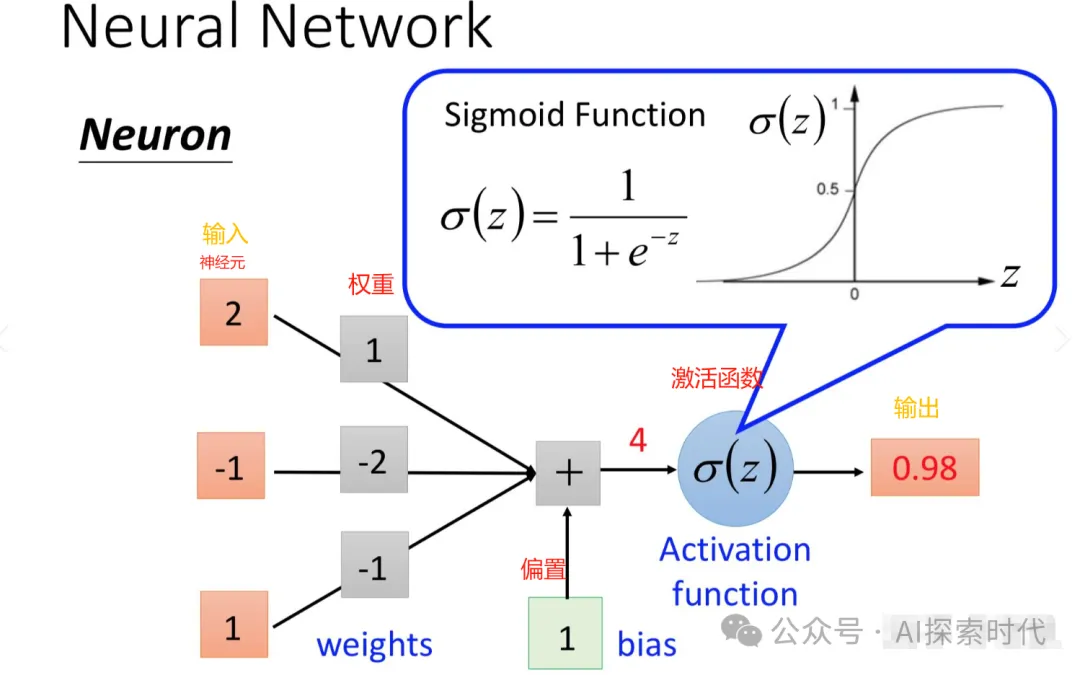
圖中左邊橙色部分作為輸入，其值來源于上層網絡神經元的輸出，每一個輸入就代表著上層的一個神經元。

這時可能有人會奇怪，一個神經元的輸出是固定值，那么如果下層網絡中有多個神經元，每個神經元都接受同樣的輸入，這樣還有什么意義？

這個就是權重的作用了，由多個上層神經元作為輸入，每個神經元都會有一個權重，不同的權重就會有不同的結果。

最簡單的神經元計算公式如下：

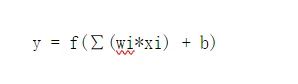
就是把每個神經元的輸入Xi乘以權重Wi累加之后，在加上當前神經元的偏置值bias。

激活函數

輸入數據經過神經元計算之后，并不是直接進行輸出，而是需要激活函數進行計算，根據閾值判斷輸出結果。公式如上圖藍色框所示。

神經元計算結果z需要作為激活函數的輸入，然后經過計算產生輸出。

比如，當激活函數的結果大于0.5時，輸入正確；小于0.5時輸出錯誤。

這就是激活函數的作用。

公式如下，紫色部分作為輸入，w表示權重；綠色部分是神經元的實現算法，最后經過紅色部分激活函數產生輸出y。

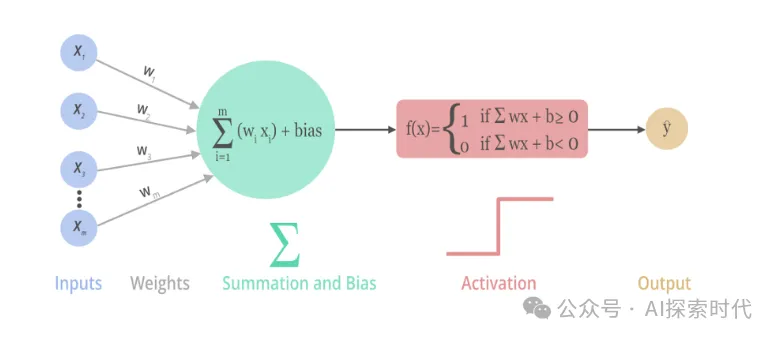
如下所示，是M-P神經元模型圖，其也是神經元的經典模型

本文轉載自公眾號AI探索時代 作者：DFires

原文鏈接：??https://mp.weixin.qq.com/s/Ine8ULkG_Wd2SaNI2tQgJg??