TPAMI 2024 | 針對節點的融合全局-局部信息的圖譜濾波方法

論文題目:
Node-oriented Spectral Filtering for Graph Neural Networks
論文作者:
Shuai Zheng, Zhenfeng Zhu, Zhizhe Liu, Youru Li, Yao Zhao
作者單位:
北京交通大學
源碼鏈接:
??https://github.com/SsGood/NFGNN/??
論文鏈接:
??https://ieeexplore.ieee.org/abstract/document/10286416/??
01 研究背景
在圖機器學習領域中,同配性(homophily)一直是一個普遍的假設,即屬于同一類的節點傾向于互相連接。然而,這一假設在很多真實的圖相關場景中其實并不成立,蛋白質結構網絡就是一個很典型的例子。
因此,研究面向異配圖數據的圖神經網絡在近幾年成為了領域內的一大主題。考慮到同配性的定義,我們提出一個觀點:下游任務與構建圖時所采用的先驗的相關性決定了一個圖的同配性程度。
具體來說,對于一個給定的拓撲結構,當其與不同下游任務的標簽分布相結合時,其同配性程度可能會非常不同。例如,學術引用網絡中,因為一篇論文更有可能引用研究相同或類似主題的論文,所以引文網絡鏈接的形成與主題分類任務是強正相關的。因此,如果我們使用論文的主題作為標簽,則則該網絡可能是同配性的;而如果我們以論文的發布年份作為標簽,引用圖可能是異配性或隨機的。
以上述假設看待圖的同配性問題,我們會發現,在標簽有限的情況下,下游任務與圖結構之間的相關性是較難預測的。因此,一個自然而然的問題是:整個圖中不同局部子圖的同配程度是否一致?
?
直觀上,假設不同區域之間總是存在多樣的子圖模式可能更為現實。因此,相比于特定于同配圖或異配圖的聚合設計,一種可以自適配圖中不同局部同配模式的 GNN,可能是更貼近實際應用需求的。
與基于空域聚合的方法相比,基于頻譜的圖神經網絡具有出色的理論解釋性和計算效率。然而,當前基于譜濾波的方法均采用了全局共享單一濾波器的學習方式。本文中,我們基于圖信號處理理論,首次嘗試探索局部自適應的譜濾波學習,以解決圖中的混合局部模式。
本文的主要貢獻如下:
- 為了深入了解實際圖的高階混合模式以及 GNN 對它們的適應性,我們從子圖同配隨機性和近鄰可聚合性兩個方面進行了實證和理論分析。
- 受廣義平移算子的啟發,我們提出了一種面向節點的譜濾波 GNN,即 NFGNN。它充分考慮了過濾器定位節點的局部子圖模式來估計濾波系數。
- 為了減輕學習面向節點的局部濾波系數的繁重負擔,我們提出了一種基于低秩近似的重參數化方法來分解濾波系數矩陣,不僅簡化了參數復雜度,而且在全局濾波和局部濾波之間進行了權衡。
02 局部同配模式分析
2.1 子圖同配隨機性
由于目標是通過節點鄰域的標簽一致性來分析圖的局部同配模式,因此我們采用了節點同配率來分析局部同配模式。首先,我們給出一階鄰域同配率和二階鄰域同配率的節點級統計直方圖的可視化。
如圖 1 所示,即使在通常被認為是同配性圖的 Cora 和 Citeseer 網絡中,也仍然存在少量的 1 跳完全異配子圖。同樣,在 Cornell 和 Actor 網絡中也有一些高同配率的子圖。此外,對于 Cornell 和 Actor 網絡,我們發現二階鄰域同配率統計直方圖與一階統計結果的顯示出一定的偏移,表明每個節點關聯的局部子圖模式通常隨著鄰域范圍的變化而變化。
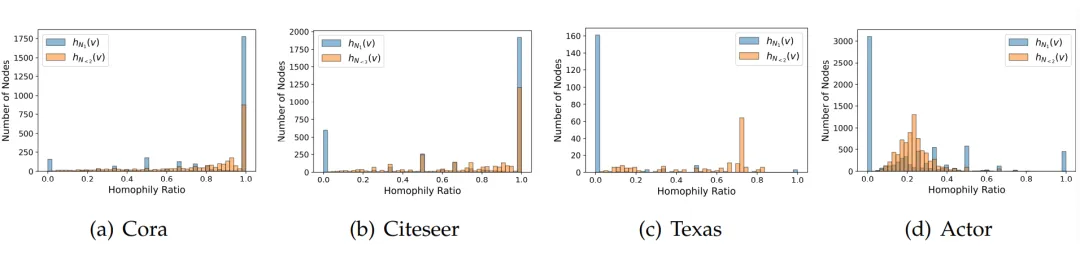
▲ 圖1:一階鄰域同配率和二階鄰域同配率的節點級統計直方圖的可視化。
值得注意的是,節點同配率的計算僅能簡單傳達鄰域節點和中心節點的標簽一致性,但忽略了鄰域標簽是呈現什么樣的分布,這對局部模式分析同樣重要。受信息論中香農熵的啟發,我們提出使用標簽熵 來衡量鄰域標簽分布:
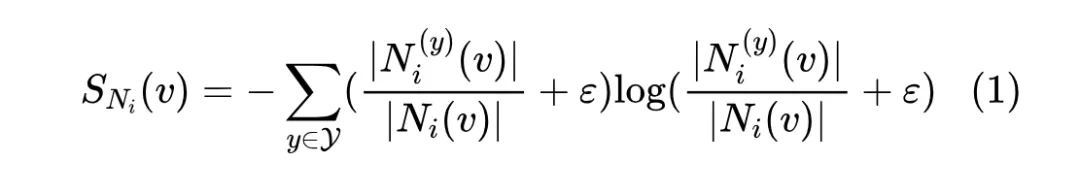
其中,,1e-10 是一個常數,用以避免溢出。標簽熵作為節點級指標,量化了給定節點的鄰域標簽分布,并指示了以該節點為中心的子圖的隨機性。顯然,當鄰居節點的標簽分布均勻時,標簽熵趨于最大。相反,如果給定節點的鄰域標簽全部屬于同一類,則標簽熵將是最小的。
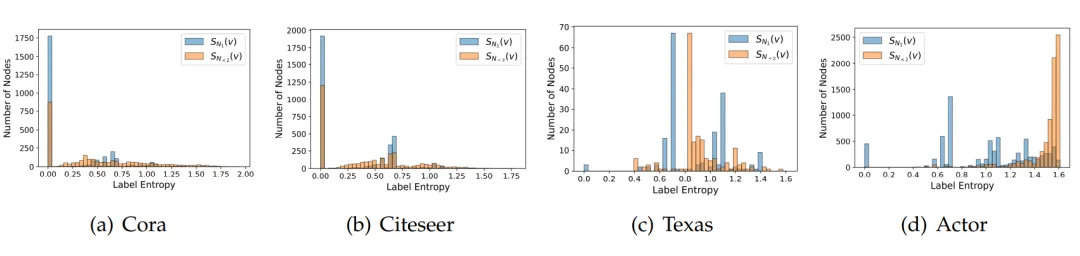
▲ 圖2:一階鄰域標簽熵和二階鄰域標簽熵的節點級統計直方圖的可視化。
如圖 2 所示,同配性圖中的大多數節點的 較低,而異配性圖中的大多數節點的 較高。此外,對于所有四個圖,與 相比, 的統計直方圖總體上向右移動。這些觀察表明,隨著鄰域范圍的增加,每個節點的鄰居標簽分布趨于均勻。更重要的是,從圖 2(c)和(d)中,可以容易地發現一些明顯的聚類現象,表明圖中可能存在幾種類型的重要局部模式。
2.2 近鄰可聚合性
?
為了便于討論近鄰的可聚集性,我們首先給出鄰域同配傾向性的定義:

我們首先理論證明了鄰域同配傾向性和鄰域標簽分布的關系:

隨即,我們還給出了隨鄰域范圍變化,鄰域同配傾向性的變化趨勢:
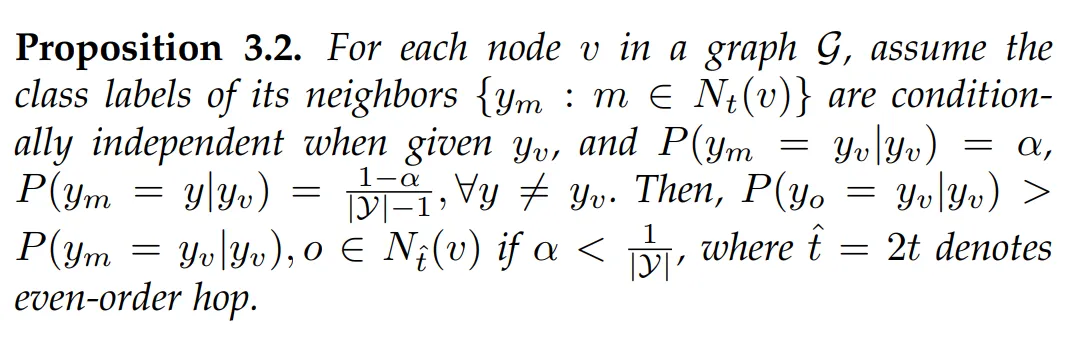
具體證明過程可見論文。
03 方法介紹
當前基于譜濾波的圖神經網絡多采用多項式參數化濾波器學習的形式。這種形式避免了特征分解,計算效率較高。另一個優點就是具有局部性,多項式的階數 K 決定了濾波器的局部化范圍,即 K 階多項式譜濾波器完全局限于節點 的 鄰域內。
但是呢,當前基于譜濾波的方法有一個顯著的特點:濾波器是全局節點通用的且頻率系數固定的單一濾波器。這個特點和多項式濾波的局部性結合在一起,就產生了新的問題:全局共享的單一濾波器相當于是在不同子圖上訓練的濾波器的trade-off。對于每個以節點為中心的子圖而言,這個全局濾波器肯定不是最差的,但應該也不是最優的。
直觀上,與學習整個圖中不同局部模式的全局共享濾波器 相比,學習特定于節點的節點濾波器 以適應其所在的局部模式似乎是更好的選擇。為此,本文重新思考這種全局一致的譜圖濾波形式,并嘗試提出一種局部化的譜濾波器學習方法來打破這一限制。
NFGNN 首先引入圖信號處理中的廣義平移算子 :
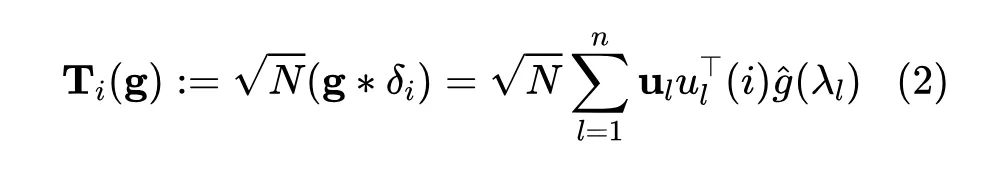
其中 表示 的第 個元素。通過對濾波信號 施加核化算子,可以使其定位在特定節點上。因此,為了自適應局部濾波的目的,首先可以通過 將濾波器信號 定位到在目標節點 上,將其定義為 ,然后與 執行譜濾波:
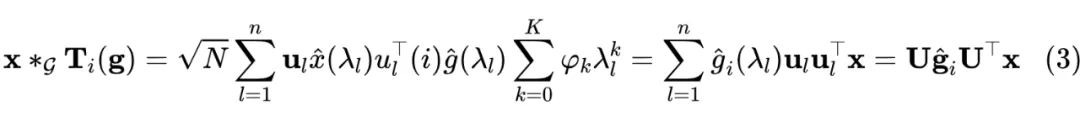
其中 ,那我們為了計算的效率問題,進一步地用多項式來參數化 ,從而得到節點導向的局部化濾波形式:
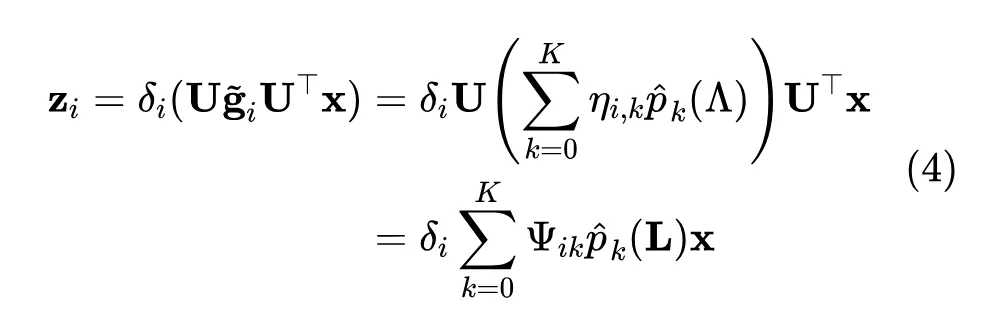
進一步地,考慮到濾波系數矩陣 的參數復雜度和優化問題,我們對其進行低秩逼近重參數化。 由兩個可訓練參數矩陣 近似,其中 和 。
可以很容易地觀察到,。這意味著 的每一列都可以視為 。因此, 相當于一組基礎濾波器,而 對應于節點 的濾波器權重。
根據 ,通過對 中的基礎濾波器進行加權組合,可以獲得專用于 的濾波器。所以,對于 ,由于其可以視為與節點相關的參數,我們應用了一個簡單但有效的非線性變換 來學習:。
04 實驗
我們在多個基準數據集上進行了全面的實驗,以評估所提出的方法的有效性。
4.1 性能對比
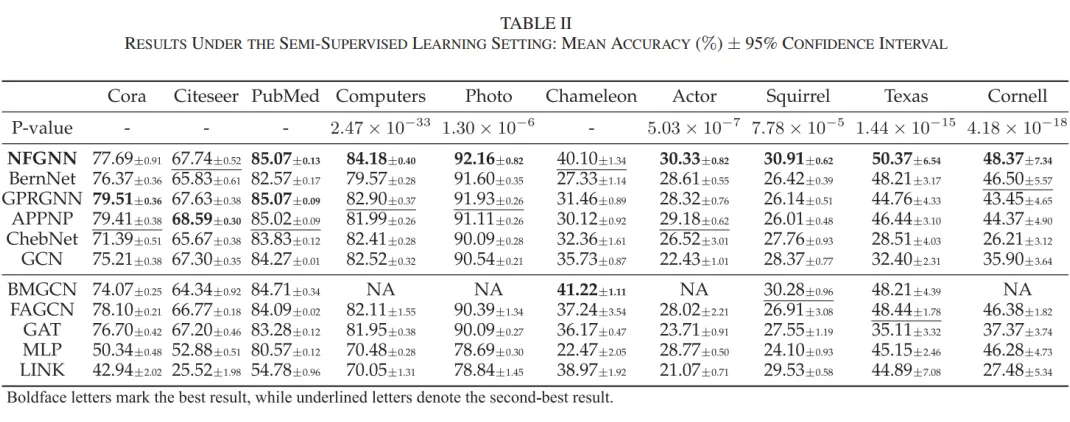
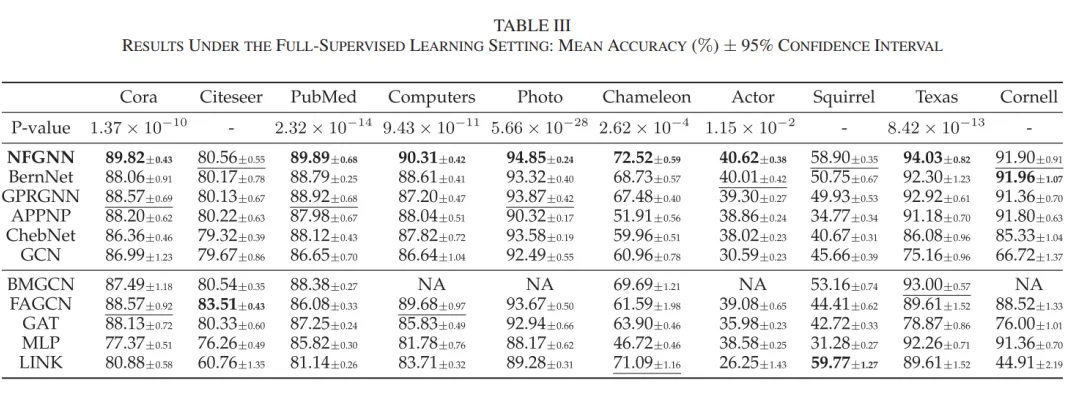
在采用稀疏劃分的半監督學習中,NFGNN 在 6 個數據集上表現出色,并在剩余的 4 個數據集上與基準模型相比顯示出可比結果。此外,在全監督學習設置下,NFGNN 在 7 個數據集上優于所有基準模型,在其他 3 個數據集上取得了可比結果。
4.2 節點級分析
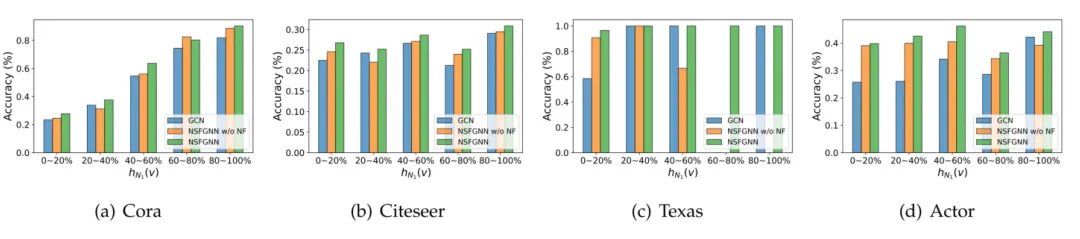
▲ 圖3 不同同配比例區間內的節點分類準確率。
本文提出的 NFGNN 旨在解決混合局部模式問題。因此,我們根據鄰近節點的同配性比例 將測試節點劃分為 5 個不同區間,并報告每個區間的平均準確率。GCN、僅有 的 NFGNN(標記為 NFGNN w/o NF)和完整的 NFGNN 的結果如圖 3 所示。
值得注意的是,NFGNN w/o NF 相當于使用切比雪夫多項式學習一個全局一致的濾波器。
與 GCN 不同,如圖 3(c)和(d)所示,NFGNN 在所有五個區間上均表現出了良好且相似的性能。這表明,只要可訓練數據量足夠,NFGNN 可以有效捕獲各種局部模式。
此外,如圖 3(a)和(b)所示,無論是 NFGNN 還是 NFGNN w/o NF 都比 GCN 在半監督節點分類任務上表現更好。這表明,即使在半監督情況下,自適應學習的濾波器也不比預設計的濾波器表現差。
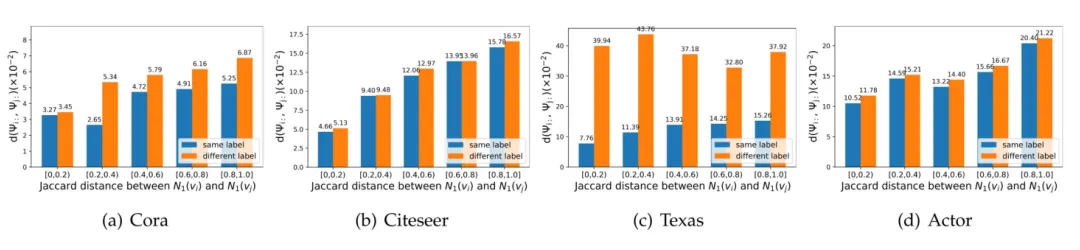
▲ 圖4 節點對 之間的濾波系數平均距離 。
正如之前討論的,局部模式也可以根據節點的鄰域子圖來分析。一般來說,如果節點的局部模式相似,那么為這些節點學習的濾波器的系數也應該相似。因此,本文中還計算了所有節點對 的 1 階鄰居的 Jaccard 相似系數 ,以衡量節點之間 1 階局部模式的相似性,然后,對于每對節點 ,根據 的區間計算平均系數距離 。
如圖 4 所示,總的來說,可以看到, 越大,相應的 越大。并且,具有相同標簽的節點對的 小于具有不同標簽的節點對。可視化結果表明,NFGNN 至少能夠學習到多種1跳局部模式的特性,符合預期。
4.3 濾波器可視化
首先根據 2 跳鄰域內的同配比率將節點劃分為三個子集:
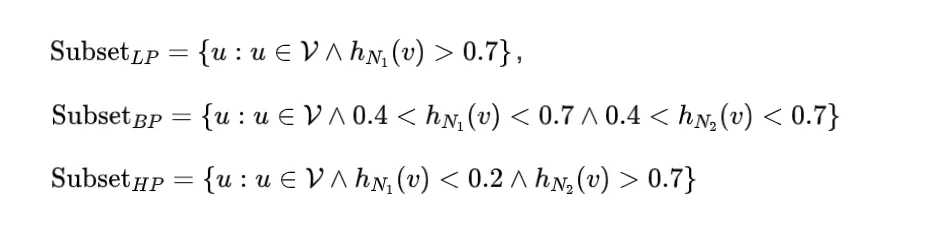
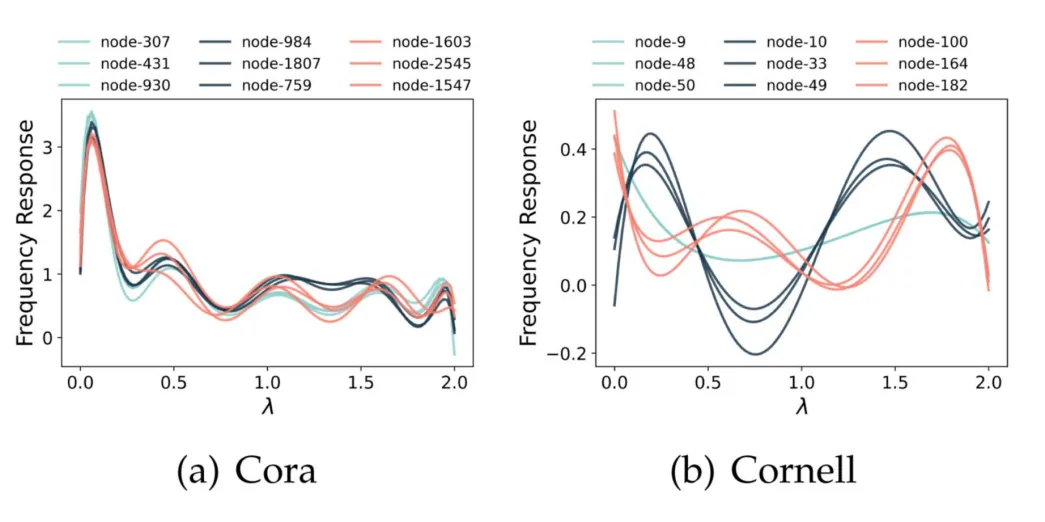
▲ 圖5 節點級濾波器可視化
05 總結
本文深入分析了圖數據中局部模式的特性及其近鄰的可聚合性。基于這些觀察,本章重新審視了基于譜的圖神經網絡(GNN)模型,并提出了 NFGNN ——一種針對節點的融合全局-局部信息的圖譜濾波方法。NFGNN 的核心優勢在于,它不同于傳統使用全局濾波器的策略,而是通過轉移至特定節點的濾波器來實現局部譜濾波,從而有效地應對局部模式的挑戰。
此外,通過引入重參數化策略,NFGNN 以一種簡單且有效的方式實現了節點導向的濾波。在多個真實世界的圖數據集上進行的實驗結果驗證了 NFGNN 在當前現有方法中的卓越性能,展示了其在處理局部圖模式方面的顯著優勢。

















