講究套路之前，先來回答三個問題。

為什么要打印樹形結構

樹形結構是算法里很常見的一種數據結構，從二叉樹到多叉樹，還有很多變種。很多涉及到算法的工作，就需要程序員自己手動實現樹形結構，但出于結構本身復雜性，不太容易做對，需要一種調試工具來檢測正確性。一般的調試手段無非就是加打印，GDB上斷點，寫測試用例等，但這些局部以及外部的調試信息對于數據結構的整體把握提供的幫助十分有限，經驗不足的程序員甚至可能會迷失在一大片調試信息的汪洋大海中找不著北。理解算法本身是一回事，自己動手是另一回事了，這跟我們理解算法的思維方式有關——對于數據結構而言，我們的感知是形象化的，比方腦海中自動出現一幅圖，動態的插入刪除，每個節點是如何變動的，平衡的時候局部是怎么旋轉的等等，對智力正常的人來說不是什么難事。但對機器來說，它要面對的是只是一堆基于狀態的指令而已，將人的形象思維轉化為狀態機，本身是一件艱難的工作，因為我們很難感知并存儲這么多狀態，這就需要工具來輔助，最好是畫出整個形狀結構，以直觀地提醒我們哪里出錯了，所謂“觀其形，見其義”。

我們知道Linux有個tree命令用來打印樹狀目錄列表，可以將某個目錄下的所有文件和子目錄一覽無遺，非常直觀，本文可以說就是為了實現這個效果，并給出源碼實現。

為什么用深度優先遍歷

主要是方便輸出。在終端輸出一般都是從左至右，從上到下，對于樹形結構來說，前者自然表達的是從根節點到葉子節點，后者自然表達的是相鄰分支，深度優先遍歷符合輸出次序。

實際上廣度優先遍歷實現起來更簡單，只要在每一層左端建立一個鏈表頭，將同一層的節點橫向串聯起來，從上到下遍歷鏈表頭數組就可以了。但考慮以下幾點：

• 我們的屏幕沒有這么寬，足以容納整棵樹，而且我們更趨向于縱向滾動瀏覽；
• 層次關系很難表示，光實現對齊就很麻煩；
• 每個節點需要維護一個額外next指針，如果這不是數據結構本身所需要的成員，對于存儲空間來說是個額外的負擔。

這也說明深度優先遍歷第二個優點，它的實現對于數據結構本身是非侵入式的。

為什么使用非遞歸遍歷

其實這是一個見仁見智的問題。遞歸還是非遞歸，不過是兩種不同的遍歷形式，不存在絕對的優劣，而且一般情況下可以相互補充。我個人選擇非遞歸出于以下幾種因素：

• 避免樹層次過多導致函數調用堆棧溢出；
• 避免C語言函數調用開銷；
• 所有狀態可見可控。

當然以上因素并不重要，開心就好。

一切皆套路，不變應萬變

既然本文講究套路，那么干脆現在就把套路給出來好了，偽代碼形式：

/* log對象 */ typedef struct node_backlog {     node指針;     回溯點位置（索引）; };  /* Dump */ void dump(tree) {     從根節點開始迭代;     初始化log堆棧;     for (; ;) {         if (節點指針為空) {             從log對象中獲取回溯點位置;             if (不存在，或無效的回溯點) {                 壓棧空節點指針;             } else {                 壓棧當前節點指針，同時記錄下一個回溯點位置;             }             if (回溯點位置索引為0) {                 輸出層次縮進、畫路徑，打印節點內容;             }             進入下一層;         } else {             if (log堆棧為空) return;             彈出log對象，獲取最近記錄的節點指針;         }     } } 

簡單吧？而且我敢說，這個套路對于所有樹形結構都是通用的，只要能夠深度遍歷。

不信我給出三個實戰例子。

目錄樹或字典樹

代碼在gist。這是個MIB樹，是管理網絡節點（設備）用的。簡要地講，它具有兩重特性：

• 節點之間的層次嵌套關系，決定了它屬于目錄層次結構；
• 節點的key具有公共前綴，使得它也類似于（或可用于）字典結構。

我們不需要關心其CRUD實現，只需要知道有一棵現成的目錄樹或者字典樹，我們如何在終端輸出它的形狀。

#define OID_MAX_LEN  64  struct node_backlog {     /* node to be backlogged */     struct mib_node *node;     /* the backtrack point, next to the orignal sub-index of the node, valid when >= 1, invalid == 0 */     int next_sub_idx; };  static inline void nbl_push(struct node_backlog *nbl, struct node_backlog **top, struct node_backlog **bottom) {     if (*top - *bottom< OID_MAX_LEN) {         (*(*top)++) = *nbl;     } }  static inline struct node_backlog * nbl_pop(struct node_backlog **top, struct node_backlog **bottom) {     return *top > *bottom? --*top : NULL; }  void mib_tree_dump(void) {     int level = 0;     oid_t id = 0;     struct mib_node *node = *dummy_root;      struct node_backlog nbl, *p_nbl = NULL;     struct node_backlog *top, *bottom, nbl_stack[OID_MAX_LEN];      top = bottom = nbl_stack;      for (; ;) {         if (node != NULL) {             /* Fetch the pop-up backlogged node's sub-id. If not backlogged, set 0. */             int sub_idx = p_nbl != NULL ? p_nbl->next_sub_idx : 0;             /* Reset backlog for the node has gone deep down */             p_nbl = NULL;              /* Backlog the node */             if (is_leaf(node) || sub_idx + 1 >= node->sub_id_cnt) {                 nbl.node = NULL;                 nbl.next_sub_idx = 0;             } else {                 nbl.node = node;                 nbl.next_sub_idx = sub_idx + 1;             }             nbl_push(*nbl, *top, *bottom);             level++;              /* Draw lines as long as sub_idx is the first one */             if (sub_idx == 0) {                 int i;                 for (i = 1; i < level; i++) {                     if (i == level - 1) {                         printf("%-8s", "+-------");                     } else {                         if (nbl_stack[i - 1].node != NULL) {                             printf("%-8s", "|");                         } else {                             printf("%-8s", " ");                         }                     }                 }                 printf("%s(%d)\n", node->name, id);             }              /* Go deep down */             id = node->sub_id[sub_idx];             node = node->sub_ptr[sub_idx];         } else {             p_nbl = nbl_pop(*top, *bottom);             if (p_nbl == NULL) {                 /* End of traversal */                 break;             }             node = p_nbl->node;             level--;         }     } } 

代碼不算復雜，就講幾個要點

深度優先遍歷要利用回溯點，就是走到一個分支的盡頭后，上溯到原先路過的某個位置，從另一個分支繼續遍歷，如果回溯到根節點，就說明遍歷結束了，所以，回溯點是必須要記錄的。問題是記錄哪個位置呢？以二叉樹為例，遍歷了左子樹后，接下來遍歷的就是右子樹，所以回溯點是右孩子；對于多叉樹，遍歷第N個分支后，接下來要遍歷N+1分支，所以回溯點是N+1；如果遍歷完最后一個分支，則需要繼續上溯尋找回溯點了。所以呢，我們就用sub_idx + 1來記錄回溯點，我們還可以利用這個屬性做個分類，值大于等于1時，回溯點有效，值等于0，回溯點無效。

關于log堆棧操作，這里使用了二級指針的技巧。這個堆棧十分小巧，所以利用函數局部變量做存儲也未嘗不可，還有不需要對外暴露數據的好處。那么對于堆棧指針，就需要傳遞二次指針來改變它。比如我們看入棧操作：

(*(*top)++) = *nbl; 

這是將log對象拷貝給top指向位置，然后將top指針上移，top和bottom的差值就是堆棧元素的數目。由于top是二級指針，所以被賦值的是**top，指針移動就是(*top)++。再來看出棧操作：

return --*top; 

先將top下移一個單位，然后返回所指向的log對象，也就是*top。

接下來該深入講解套路了，首先，根節點設置成了dummy，這是一個虛擬節點，是為了保證最上層只有一個節點而使用的編碼技巧，好比tree命令輸出目錄樹總是從當前目錄“.”開始。由于第一次進入循環，log堆棧為空，不存在所謂回溯點，我們將回溯位置索引設為0，這有兩重含義，一來表示該回溯點無效或不存在，二來既然沒有回溯，那么接下來就從當前節點的第一個分支開始遍歷。

然后我們將遍歷過的節點壓棧，這里也是有區分的：如果當前是葉子節點，或者所有分支都遍歷完了，那么應該繼續上溯去尋找回溯點，我們就將回溯點設為無效后壓棧；否則就將當前節點設為回溯點，并記錄位置索引后壓棧。

畫線輸出部分稍后講。我們根據前面獲取的索引sub_idx進入下一層，直到觸底回溯，這時從log堆棧彈出回溯點，pop有三種情況：由于第一個壓棧為根節點，堆棧為空表示回溯到原點，也就標志著整個遍歷結束，退出循環；否則查看回溯點是否為NULL，如果空如前所述繼續上溯；如果存在有效回溯點，則將回溯位置索引取出，繼續下一輪遍歷循環。

最后講終端輸出。前面說過每一行從左至右的輸出的是樹的層次遍歷，其實就是遍歷log堆棧；換行輸出就是樹的分支遍歷，就是每一輪循環。輸出內容主要是三個符號：縮進、分支和節點內容。我們作如下策略：

• 縮進：當堆棧里回溯點無效，則不存在分支，打印空格，八個字符對齊；
• 分支：當堆棧里回溯點有效，表示存在分支，打印“|”和空格，八個字符對齊；
• 節點：當堆棧遍歷到最后一個元素，表示后面將要輸出節點內容，打印“+---”，八個字符對齊，后面跟節點內容。

當然你也可以自定義打印策略以便輸出更美觀。好了，說了一大堆，看效果吧，運行程序，一目了然。

<center>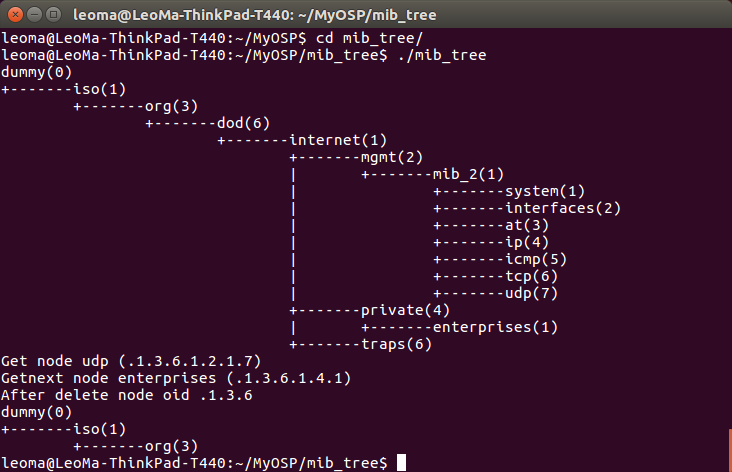</center>

B+樹

代碼在此。B+樹是關系數據庫常用的底層數據結構，實現起來相當恐怖，所幸本文不講這些，這里只是將B+樹作為多叉樹示范如何打印，特別是葉子節點和非葉子節點本身定義不同的情況下。從輸出實現上我們發現，log對象記錄的只是節點的指針和回溯位置，同數據節點本身沒有關系。我們幾乎可以原封不動地把上面的代碼搬過來，運行效果如下：

</center> 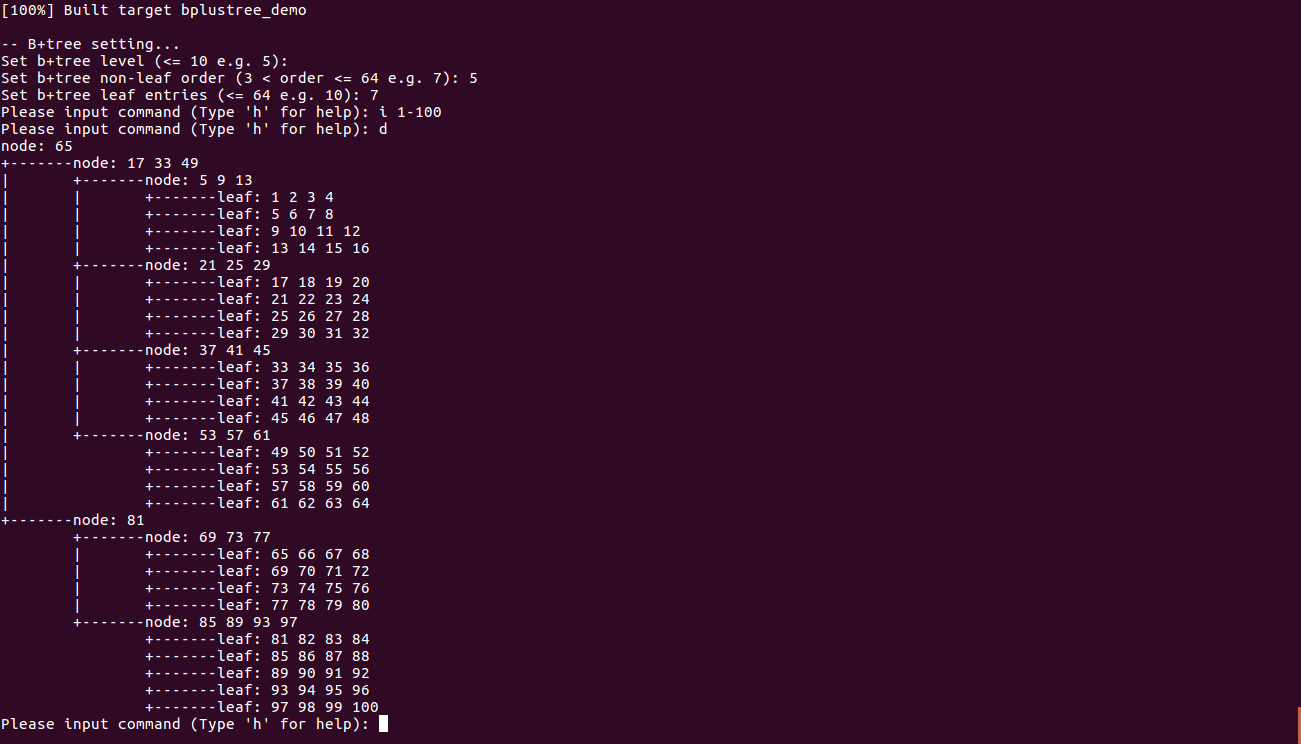</center>

從形狀上可以看到B+樹的真實數據都存儲在葉子節點，而且整棵樹是平衡的。

紅黑樹（二叉樹）

代碼在此。理解了多叉樹的實現，二叉樹不過是一種特殊簡化形式罷了。本文挑選了紅黑樹為代表，代碼自己懶得寫了，直接拿Nginx源碼。

觀察得出，二叉樹關于回溯點的位置其實只有右邊分支，也就是說回溯位置索引只有一個值，就是1。這樣一來我們可以做個簡化，將左分支索引設為0表示無效回溯位置，右分支索引設為1表示有效回溯位置，代碼可以這樣寫：

#define RBTREE_MAX_LEVEL   64 #define RBTREE_LEFT_INDEX  0 #define RBTREE_RIGHT_INDEX 1  void rbtree_dump(struct rbtree *tree) {     int level = 0;     struct rbnode *node = tree->root, *sentinel = tree->sentinel;     struct node_backlog nbl, *p_nbl = NULL;     struct node_backlog *top, *bottom, nbl_stack[RBTREE_MAX_LEVEL];      top = bottom = nbl_stack;      for (; ;) {         if (node != sentinel) {             /* Fetch the pop-up backlogged node's sub-id. If not backlogged, set 0. */             int sub_index = p_nbl != NULL ? p_nbl->next_sub_idx : RBTREE_LEFT_INDEX;             /* backlog should be reset since node has gone deep down */             p_nbl = NULL;              /* Backlog the node */             if (is_leaf(node, sentinel) || sub_index == RBTREE_RIGHT_INDEX) {                 nbl.node = sentinel;                 nbl.next_sub_idx = RBTREE_LEFT_INDEX;             } else {                 nbl.node = node;                 nbl.next_sub_idx = RBTREE_RIGHT_INDEX;             }             nbl_push(&nbl, &top, &bottom);             level++;              /* Draw lines as long as sub_idx is the first one */             if (sub_index == RBTREE_LEFT_INDEX) {                 /* Print intent, branch and node content... */             }              /* Move down according to sub_idx */             node = sub_index == RBTREE_LEFT_INDEX ? node->left : node->right;         } else {             /* Pop up the node backlog... */         }     } } 

讓我們看一看輸出效果……等等，我們發現對于二叉樹，右孩子在左孩子的下一行打印，視覺上有點不習慣是嗎？還好我貼心地將LEFT_INDEX和RIGHT_INDEX交換了一下次序，右孩子就先于左孩子輸出了，這樣一來你就可以歪著腦袋直觀地看二叉樹了（笑），同時我們還知道，“翻轉”一棵二叉樹是多么容易（笑）。

<center>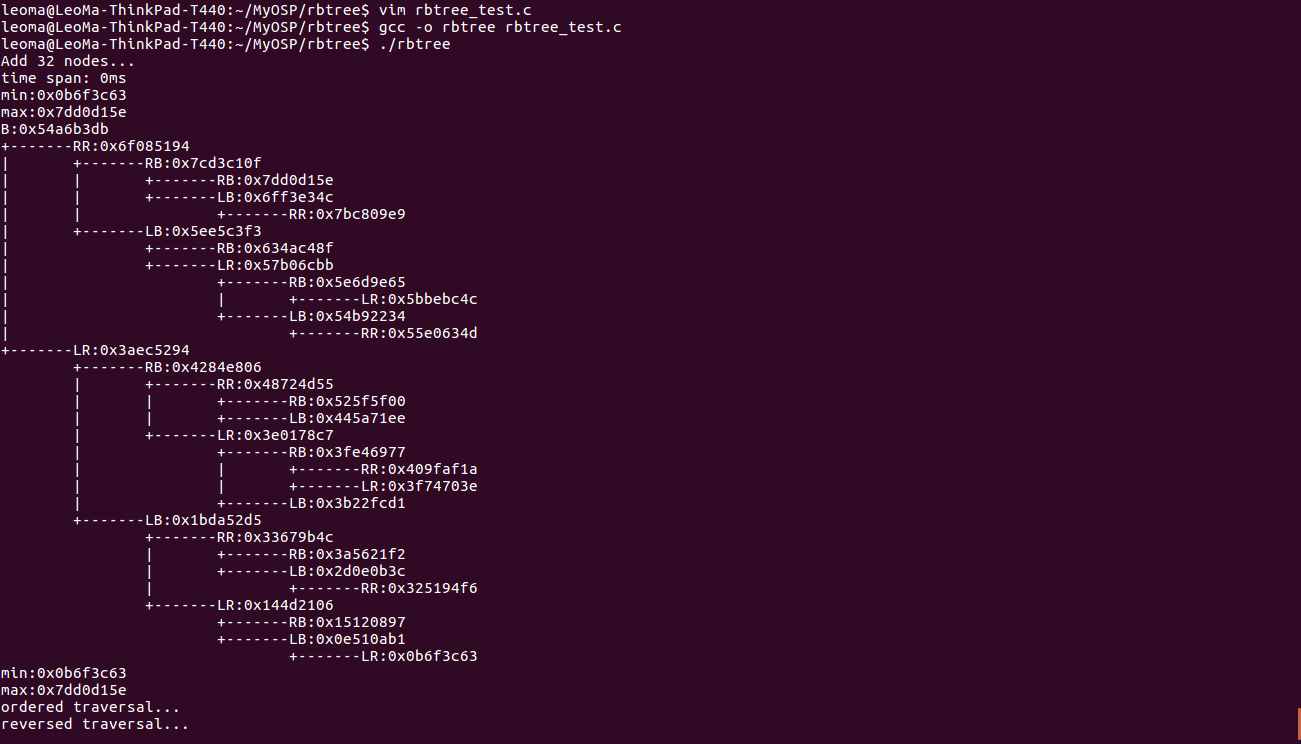</center>

工欲善其事，必先利其器。學會了樹形結構打印工具，針對這樣的數據結構，只有你寫不了的，沒有你寫不對的。最后給出一個思考題：如何用遞歸形式實現打印樹形結構？（提示：利用參數傳遞）

參考源碼

目錄樹 B+樹 紅黑樹