深入理解游戲中尋路算法
如果你玩過MMOARPG游戲,比如魔獸,你會發(fā)現(xiàn)人物行走會很有趣,為了模仿人物行走的真實(shí)體驗(yàn),他們會選擇最近路線達(dá)到目的地,期間會避開高山或者湖水,繞過箱子或者樹林,直到走到你所選定的目的地。
這種看似尋常的尋路在程序?qū)崿F(xiàn)起來就需要一定的尋路算法來解決,如何在最短時(shí)間內(nèi)找到一條路徑最短的路線,這是尋路算法首先要考慮的問題。
在這篇文章中我們會循序漸進(jìn)來講解尋路算法是如何演進(jìn)的,你會看到一種算法從簡單到高效所遇到的問題,以及精進(jìn)的過程,帶著問題來閱讀,理解更快。
本篇主要包含以下內(nèi)容:
1、圖
2、寬度***搜索,
3、Dijkstra 算法,
4、貪心算法,
****搜索算法,
6、B*搜索算法,
1、游戲中的人物是如何尋路的
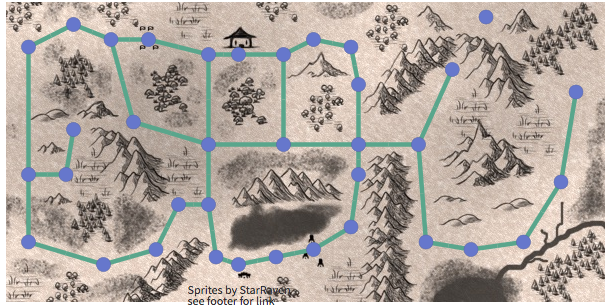
你所看到的人物行走方式:
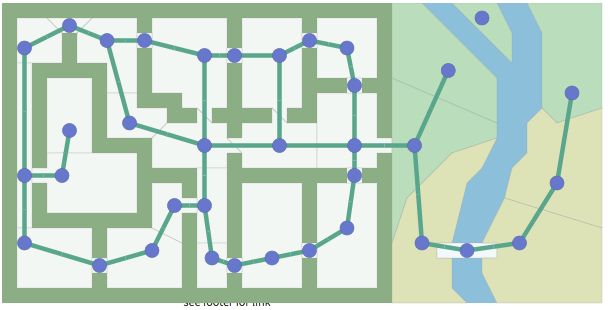
開發(fā)人員實(shí)際所看到的方式:
或者是這種:
對于一張地圖,開發(fā)人員需要通過一定的方案將其轉(zhuǎn)換為數(shù)據(jù)對象,常見的就是以上這種把地圖切個(gè)成網(wǎng)格,當(dāng)然了地圖的劃分方式不一定非要用網(wǎng)格這種方式,采用多邊形方式也可以,這取決于你的游戲,一般情況下,同等面積的地圖采用更少的頂點(diǎn),尋路算法會更快。尋路中常用的數(shù)據(jù)結(jié)構(gòu)就是圖,以下我們先來了解一下。
2、圖
在講尋路算法之前我們先了解一種數(shù)據(jù)結(jié)構(gòu)—圖,數(shù)據(jù)結(jié)構(gòu)是我們進(jìn)行算法運(yùn)算的基礎(chǔ),好的數(shù)據(jù)結(jié)構(gòu)除了方便我們理解算法,還會提升算法的效率。網(wǎng)格某種意義上也是圖的演變,只是圖形變了而已,理解了圖的概念可以幫助我們更好理解尋路算法。
圖的基本定義:
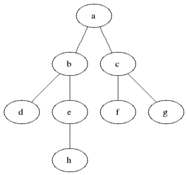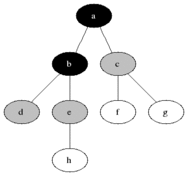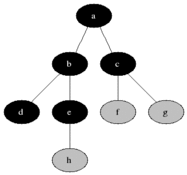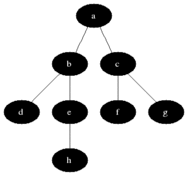
圖的正式表達(dá)式是G=(V,E),V是代表頂點(diǎn)的集合,E和V是一種二元關(guān)系,可以理解為邊,比如有條邊從頂點(diǎn)U到頂點(diǎn)V結(jié)束,那么E可以用(u,v)來表示這條邊。具體的有向圖和無向圖,也是邊是否有方向來區(qū)分。為了方便理解,我們文中所有的數(shù)據(jù)演示都是基于網(wǎng)格地圖來進(jìn)行講解,以下是幾種關(guān)系梳理,以A為頂點(diǎn),BCDE為子頂點(diǎn),我們可以把每個(gè)格子也看是一個(gè)頂點(diǎn)。
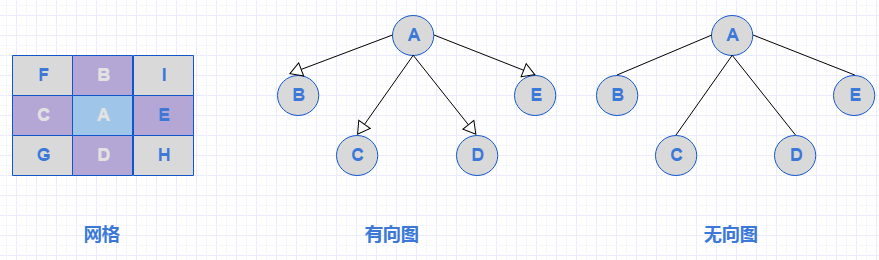
3、搜索算法
對一個(gè)圖進(jìn)行搜索意味著按照某種特定的順序依次訪問其頂點(diǎn)。對于多圖算法來說,廣度優(yōu)先算法和深度優(yōu)先搜索算法都十分重要,因?yàn)樗鼈兲峁┝艘惶紫到y(tǒng)地訪問圖數(shù)據(jù)結(jié)構(gòu)的方法。我們著重講解廣度優(yōu)先搜索算法。
深度優(yōu)先搜索
深度優(yōu)先算法和最小路徑關(guān)系不大,我們只簡單介紹。
深度優(yōu)先搜索算法(簡稱DFS)是一種用于遍歷或搜索樹或圖的算法。沿著樹的深度遍歷樹的節(jié)點(diǎn),盡可能深的搜索樹的分支。當(dāng)節(jié)點(diǎn)v的所在邊都己被探尋過,搜索將回溯到發(fā)現(xiàn)節(jié)點(diǎn)v的那條邊的起始節(jié)點(diǎn)。這一過程一直進(jìn)行到已發(fā)現(xiàn)從源節(jié)點(diǎn)可達(dá)的所有節(jié)點(diǎn)為止。
廣度優(yōu)先搜索
廣度優(yōu)先搜索算法(簡稱BFS)又稱為寬度優(yōu)先搜索,是一種圖形搜索算法,很適合用來探討最短路徑的***個(gè)模型,我們會順著這個(gè)思路往下講。
BFS是一種盲目搜尋法,目的是系統(tǒng)地展開并檢查圖中的所有節(jié)點(diǎn),以找尋結(jié)果。換句話說,它并不考慮結(jié)果的可能位址,徹底地搜索整張圖,直到找到結(jié)果為止它的步驟如下:
- 首先將根節(jié)點(diǎn)放入隊(duì)列中。
- 從隊(duì)列中取出***個(gè)節(jié)點(diǎn),并檢驗(yàn)它是否為目標(biāo)。
- 如果找到目標(biāo),則結(jié)束搜尋并回傳結(jié)果。
- 否則將它所有尚未檢驗(yàn)過的直接子節(jié)點(diǎn)(鄰節(jié)點(diǎn))加入隊(duì)列中。
- 若隊(duì)列為空,表示整張圖都檢查過了——亦即圖中沒有欲搜尋的目標(biāo)。結(jié)束搜尋并回傳“找不到目標(biāo)”。
網(wǎng)格:

我們看下代碼(js):
var frontier = new Array();
frontier.put(start);
var visited = new Array();
visited[start] = true;
while(frontier.length>0){
current = frontier.get();
//查找周圍頂點(diǎn)
for(next in graph.neighbors(current)){
var notInVisited = visited.indexOf(next)==-1;
//沒有訪問過
if(notInVisited) {
frontier.put(next);
visited[next] = true;
}
}
}
從上可以發(fā)現(xiàn),寬度搜索就是以開始頂點(diǎn)為起點(diǎn),訪問其子節(jié)點(diǎn)(在網(wǎng)格中是訪問周圍節(jié)點(diǎn)),然后不斷的循環(huán)這個(gè)過程,直到找到目標(biāo),這種算法比較符合常規(guī)邏輯,把所有的的頂點(diǎn)全部枚舉一遍。不過這種方式也有很明顯的缺點(diǎn)。
缺陷:
1、效率底下, 時(shí)間復(fù)雜度是:T(n) = O(n^2)
2、每個(gè)頂點(diǎn)之間沒有權(quán)值,無法定義優(yōu)先級,不能找到***路線。比如遇到水域需要繞過行走,在寬度算法里面無法涉及。
如何解決這個(gè)問題?我們來看Dijkstra 算法。
4、Dijkstra 算法
寬度優(yōu)先搜索算法,解決了起始頂點(diǎn)到目標(biāo)頂點(diǎn)路徑規(guī)劃問題,但不是***以及合適的,因?yàn)樗倪厸]有權(quán)值(比如距離),路徑無法進(jìn)行估算比較***解。為何權(quán)值這么重要,因?yàn)檎鎸?shí)環(huán)境中,2個(gè)頂點(diǎn)之間的路線并非一直都是直線,需要繞過障礙物才能達(dá)到目的地,比如森林,湖水,高山,都需要繞過而行,并非直接穿過。
比如我采用寬度優(yōu)先算法,遇到如下情況,他會直接穿過障礙物(綠色部分 ),明顯這個(gè)不是我們想要的結(jié)果:
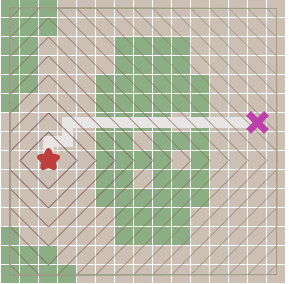
解決痛點(diǎn):
尋找圖中一個(gè)頂點(diǎn)到另一個(gè)頂點(diǎn)的最短以及最小帶權(quán)路徑是非常重要的提煉過程。為每個(gè)頂點(diǎn)之間的邊增加一個(gè)權(quán)值,用來跟蹤所選路徑的消耗成本,如果位置的新路徑比先前的***路徑更好,我們將添加它,規(guī)劃到新的路線中。
Dijkstra 算法基于寬度優(yōu)先算法進(jìn)行改進(jìn),把當(dāng)前看起來最短的邊加入最短路徑樹中 ,利用貪心算法計(jì)算并最終能夠產(chǎn)生***結(jié)果的算法。具體步驟如下:
1、每個(gè)頂點(diǎn)都包含一個(gè)預(yù)估值cost(起點(diǎn)到當(dāng)前頂點(diǎn)的距離),每條邊都有權(quán)值v ,初始時(shí),只有起始頂點(diǎn)的預(yù)估值cost為0,其他頂點(diǎn)的預(yù)估值d都為無窮大 ∞。
2、查找cost值最小的頂點(diǎn)A,放入path隊(duì)列
3、循環(huán)A的直接子頂點(diǎn),獲取子頂點(diǎn)當(dāng)前cost值命名為current_cost,并計(jì)算新路徑new_cost,new_cost=父節(jié)點(diǎn)A的cost+v(父節(jié)點(diǎn)到當(dāng)前節(jié)點(diǎn)的邊權(quán)值),如果new_cost<current_cost,當(dāng)前頂點(diǎn)的cost=new_cost
4、重復(fù)2,3直至沒有頂點(diǎn)可以訪問.
我們看下圖例:
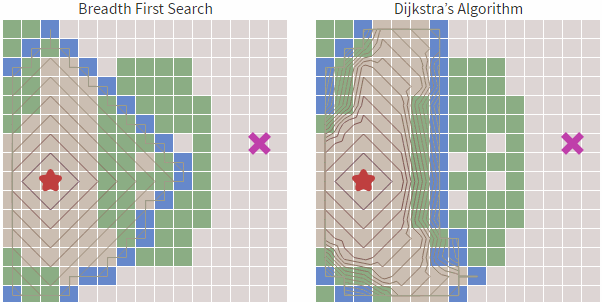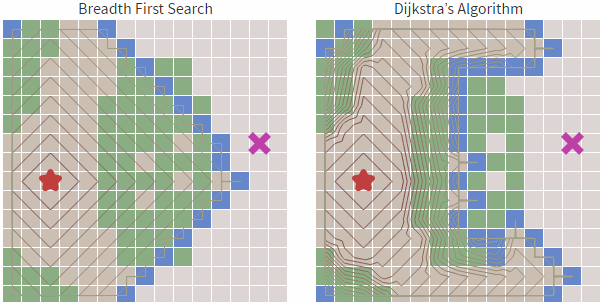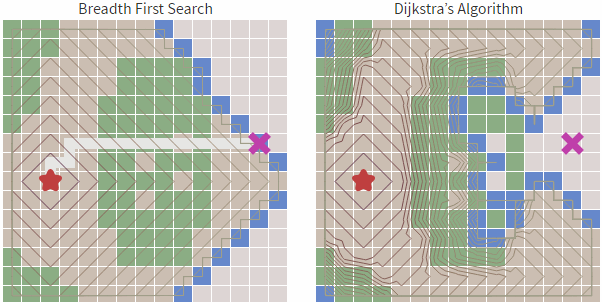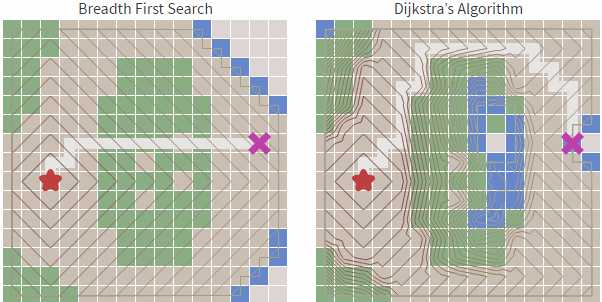
我們看下代碼(js):
var frontier = new PriorityQueue();
frontier.put(start);
path = new Array();
//每個(gè)頂點(diǎn)路徑消耗
cost_so_far = new Array();
path[start] = 0;
cost_so_far[start] = 0
while(frontier.length>0){
current = frontier.get();
if current == goal:
break
//查找周圍節(jié)點(diǎn)
for(next in graph.neighbors(current)){
var notInVisited = visited.indexOf(next)==-1;
var new_cost = cost_so_far[current] + graph.cost(current, next);
//沒有訪問過或者路徑更近
if(notInVisited || new_cost < cost_so_far[next]) {
cost_so_far[next] = new_cost;
priority = new_cost;
frontier.put(next, priority);
path[next] = current;
}
}
}
我們看到雖然Dijkstra 算法 雖然相對于寬度優(yōu)先搜索更加智能,基于cost_so_far ,可以規(guī)避路線比較長或者無法行走的區(qū)域,但依然會存在盲目搜索的傾向,我們在地圖中常見的情況是查找目標(biāo)和起始點(diǎn)的路徑,具有一定的方向性,而Dijkstra 算法從上述的圖中可以看到,也是基于起點(diǎn)向子節(jié)點(diǎn)全方位擴(kuò)散。
缺點(diǎn):
1、運(yùn)行時(shí)間復(fù)雜度是:T(n) = O(V^2),其中V為頂點(diǎn)個(gè)數(shù)。效率上并不高
2、目標(biāo)查找不具有方向性
如何解決讓搜索不是全盤盲目瞎找?我們來看Greedy Best First Search算法(貪婪***優(yōu)先搜索)。
5、貪婪***優(yōu)先搜索
在Dijkstra算法中,我已經(jīng)發(fā)現(xiàn)了其最終要的缺陷,搜索存在盲目性。在這里,我們只針對這個(gè)痛點(diǎn),采用貪婪***優(yōu)先搜索來解決。如何解決?我們只需稍微改變下觀念即可,在Dijkstra算法中,優(yōu)先隊(duì)列采用的是,每個(gè)頂點(diǎn)到起始頂點(diǎn)的預(yù)估值來進(jìn)行排序。在貪婪***優(yōu)先搜索中 ,
解決痛點(diǎn):
我們采用每個(gè)頂點(diǎn)到目標(biāo)頂點(diǎn)的距離進(jìn)行排序。一個(gè)采用離起始頂點(diǎn)的距離來排序,一個(gè)采用離目標(biāo)頂點(diǎn)距離排序(離目標(biāo)的遠(yuǎn)近排序)
哪個(gè)更快?我們看下圖(左邊寬度優(yōu)先,右邊貪婪優(yōu)先):
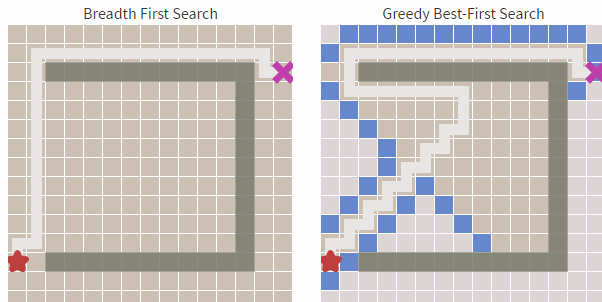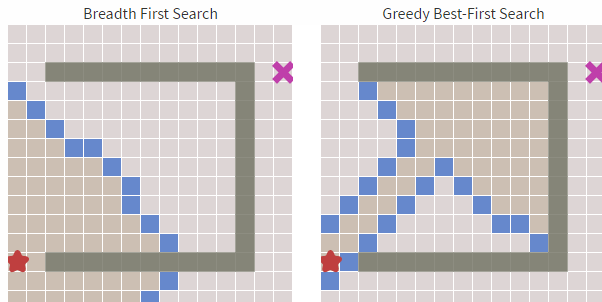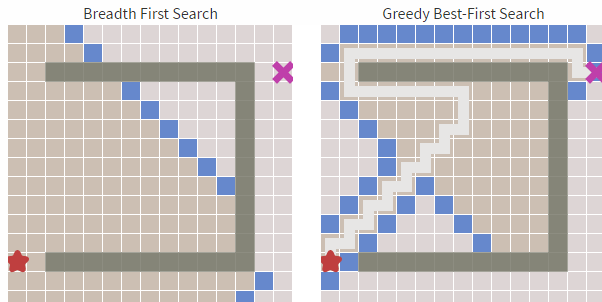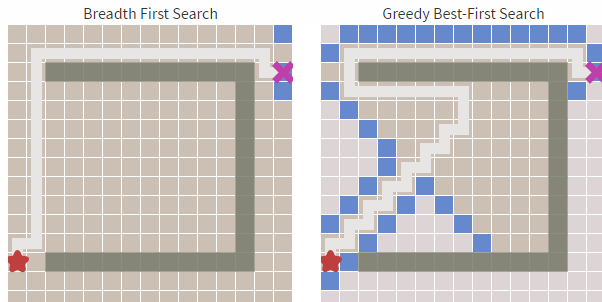
從上圖中我們可以明顯看到右邊的算法(貪婪***優(yōu)先搜索 )尋找速度要快于左側(cè),雖然它的路徑不是***和最短的,但障礙物最少的時(shí)候,他的速度卻足夠的快。這就是貪心算法的優(yōu)勢,基于目標(biāo)去搜索,而不是完全搜索。
我們看下算法(js):
frontier = new PriorityQueue();
frontier.put(start, 0)
came_from = new Array();
came_from[start] = 0;
while(frontier.length>0){
current = frontier.get()
if current == goal:
break
for(next in graph.neighbors(current)){
var notInVisited = visited.indexOf(next)==-1;
//沒有訪問過
if(notInVisited ) {
//離目標(biāo)的距離 ,距離越近優(yōu)先級越高
priority = heuristic(goal, next);
frontier.put(next, priority);
came_from[next] = current;
}
}
}
function heuristic(a, b){
//離目標(biāo)的距離
return abs(a.x - b.x) + abs(a.y - b.y)
}
缺點(diǎn):
1.路徑不是最短路徑,只能是較優(yōu)
如何在搜索盡量少的頂點(diǎn)同時(shí)保證最短路徑?我們來看A*算法。
6、A*算法
從上面算法的演進(jìn),我們逐漸找到了最短路徑和搜索頂點(diǎn)最少數(shù)量的兩種方案,Dijkstra 算法和 貪婪***優(yōu)先搜索。那么我們有沒有可能汲取兩種算法的優(yōu)勢,令尋路搜索算法即便快速又高效?
答案是可以的,A*算法正是這么做了,它吸取了Dijkstra 算法中的cost_so_far,為每個(gè)邊長設(shè)置權(quán)值,不停的計(jì)算每個(gè)頂點(diǎn)到起始頂點(diǎn)的距離,以獲得最短路線,同時(shí)也汲取貪婪***優(yōu)先搜索算法中不斷向目標(biāo)前進(jìn)優(yōu)勢,并持續(xù)計(jì)算每個(gè)頂點(diǎn)到目標(biāo)頂點(diǎn)的距離,以引導(dǎo)搜索隊(duì)列不斷想目標(biāo)逼近,從而搜索更少的頂點(diǎn),保持尋路的高效。
解決痛點(diǎn):
A*算法的優(yōu)先隊(duì)列排序方式基于F值:
F=cost(頂點(diǎn)到起始頂點(diǎn)的距離 )+heuristic(頂點(diǎn)到目標(biāo)頂點(diǎn)的距離 )
我們看下算法(js):
var frontier = new PriorityQueue();
frontier.put(start);
path = new Array();
cost_so_far = new Array();
path[start] = 0;
cost_so_far[start] = 0
while(frontier.length>0){
current = frontier.get()
if current == goal:
break
for(next in graph.neighbors(current)){
var notInVisited = visited.indexOf(next)==-1;
var new_cost = cost_so_far[current] + graph.cost(current, next);
//沒有訪問過而且路徑更近
if(notInVisited || new_cost < cost_so_far[next]) {
cost_so_far[next] = new_cost
//隊(duì)列優(yōu)先級= new_cost(頂點(diǎn)到起始頂點(diǎn)的距離 )+heuristic(頂點(diǎn)到目標(biāo)頂點(diǎn)的距離 )
priority = new_cost + heuristic(goal, next)
frontier.put(next, priority)
path[next] = current
}
}
}
function heuristic(a, b){
//離目標(biāo)的距離
return abs(a.x - b.x) + abs(a.y - b.y)
}
以下分別是Dijkstra算法,貪心算法,以及A*算法的尋路雷達(dá)圖,其中格子有數(shù)字標(biāo)識已經(jīng)被搜索了,可以對比下三種效率:
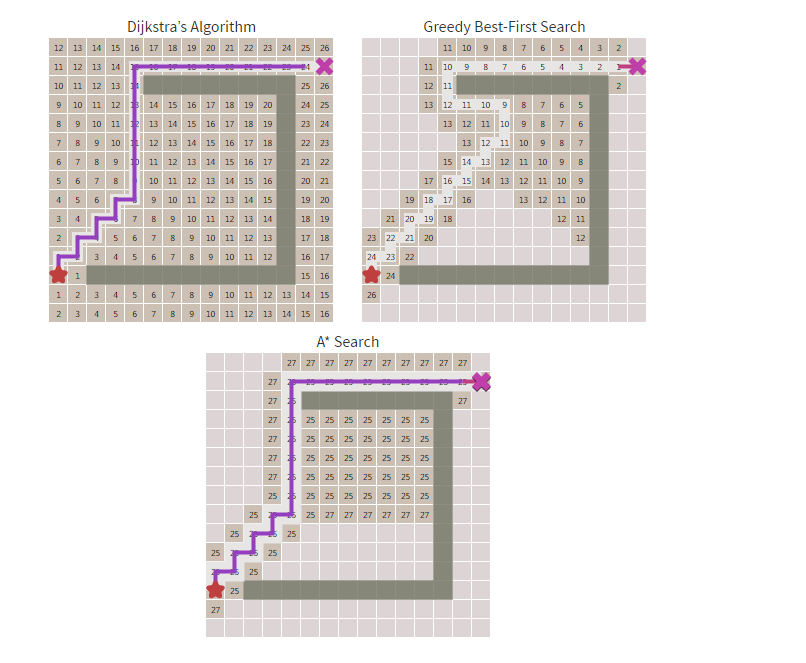
7、B*算法
B*算法是一種比A*算法更高效的算法, 適用于游戲中怪物的自動尋路,其效率遠(yuǎn)遠(yuǎn)超過A*算法,經(jīng)過測試,效率是普通A*算法的幾十上百倍。B*算法不想介紹了,自己去google下吧,
通過以上算法不斷的演進(jìn),我們可以看出每一種算法的局限,以及延伸出的新算法中出現(xiàn)的解決方式,希望方便你的理解。