本文介紹了多種激活函數，并且對比了激活函數的優劣。本文假設你對人工神經網絡(AAN)有基本了解，如果沒有，推薦先閱讀機器之心介紹過的相關文章：DNN 概述論文：詳解前饋、卷積和循環神經網絡技術

1. 什么是激活函數?

生物神經網絡啟發了人工神經網絡的發展。但是，ANN 并非大腦運作的近似表示。不過在我們了解為什么在人工神經網絡中使用激活函數之前，先了解生物神經網絡與激活函數的相關性是很有用處的。

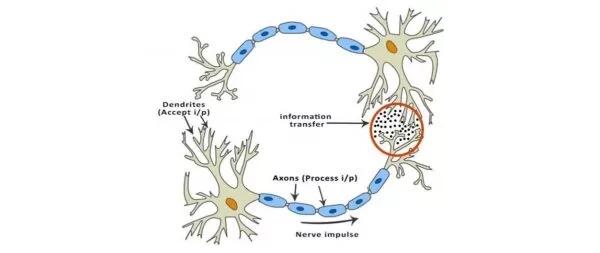
典型神經元的物理結構包括細胞體(cell body)、向其他神經元發送信號的軸突(axon)和接收其他神經元發送的信號或信息的樹突(dendrites)。

生物神經網絡

上圖中，紅色圓圈代表兩個神經元交流的區域。神經元通過樹突接收來自其他神經元的信號。樹突的權重叫作突觸權值(synaptic weight)，將和接收的信號相乘。來自樹突的信號在細胞體內不斷累積，如果信號強度超過特定閾值，則神經元向軸突傳遞信息。如未超過，則信號被該神經元「殺死」，無法進一步傳播。

激活函數決定是否傳遞信號。在這種情況下，只需要帶有一個參數(閾值)的簡單階梯函數。現在，當我們學習了一些新的東西(或未學習到什么)時，一些神經元的閾值和突觸權值會發生改變。這使得神經元之間產生新的連接，大腦學會新的東西。

讓我們再次理解這一概念，不過這次要使用人工神經元。

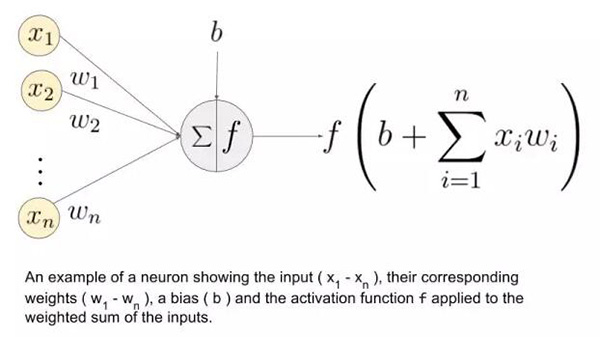
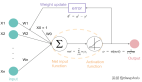
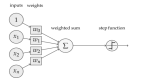
上圖中(x_1, ..., x_n)是信號向量，它和權重(w_1, ..., w_n)相乘。然后再累加(即求和 + 偏置項 b)。最后，激活函數 f 應用于累加的總和。

注意：權重(w_1, ..., w_n)和偏置項 b 對輸入信號進行線性變換。而激活函數對該信號進行非線性變換，這使得我們可以任意學習輸入和輸出之間的復雜變換。

過去已經出現了很多種函數，但是尋找使神經網絡更好更快學習的激活函數仍然是活躍的研究方向。

2. 神經網絡如何學習?

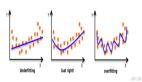
我們有必要對神經網絡如何學習有一個基本了解。假設網絡的期望輸出是 y(標注值)，但網絡實際輸出的是 y'(預測值)。預測輸出和期望輸出之間的差距(y - y')可以轉化成一種度量，即損失函數(J)。神經網絡犯大量錯誤時，損失很高;神經網絡犯錯較少時，損失較低。訓練目標就是找到使訓練集上的損失函數最小化的權重矩陣和偏置向量。

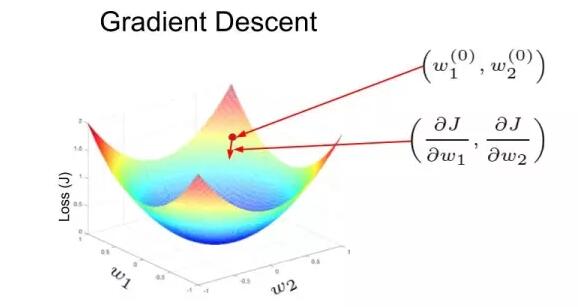
在下圖中，損失函數的形狀像一個碗。在訓練過程的任一點上，損失函數關于梯度的偏導數是那個位置的梯度。沿偏導數預測的方向移動，就可以到達谷底，使損失函數最小化。使用函數的偏導數迭代地尋找局部極小值的方法叫作梯度下降。

人工神經網絡中的權重使用反向傳播的方法進行更新。損失函數關于梯度的偏導數也用于更新權重。從某種意義上來說，神經網絡中的誤差根據求導的鏈式法則執行反向傳播。這通過迭代的方式來實施，經過多次迭代后，損失函數達到極小值，其導數變為 0。

我們計劃在其他文章中介紹反向傳播。這里主要指出的就是訓練過程中出現的求導步驟。

3. 激活函數的類型

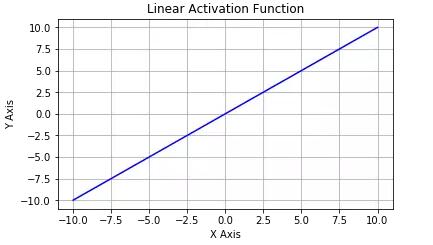
線性激活函數：這是一種簡單的線性函數，公式為：f(x) = x。基本上，輸入到輸出過程中不經過修改。

線性激活函數

非線性激活函數：用于分離非線性可分的數據，是最常用的激活函數。非線性方程控制輸入到輸出的映射。非線性激活函數有 Sigmoid、Tanh、ReLU、LReLU、PReLU、Swish 等。下文中將詳細介紹這些激活函數。

非線性激活函數

4. 為什么人工神經網絡需要非線性激活函數?

神經網絡用于實現復雜的函數，非線性激活函數可以使神經網絡隨意逼近復雜函數。沒有激活函數帶來的非線性，多層神經網絡和單層無異。

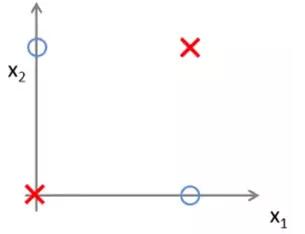
現在我們來看一個簡單的例子，幫助我們了解為什么沒有非線性，神經網絡甚至無法逼近異或門(XOR gate)、同或門(XNOR gate)等簡單函數。下圖是一個異或門函數。叉和圈代表了數據集的兩個類別。當 x_1、x_2 兩個特征一樣時，類別標簽是紅叉;不一樣，就是藍圈。兩個紅叉對于輸入值 (0,0) 和 (1,1) 都有輸出值 0，兩個藍圈對于輸入值 (0,1) 和 (1,0) 都有輸出值 1。

異或門函數的圖示

從上圖中，我們可以看到數據點非線性可分。也就是說，我們無法畫出一條直線使藍圈和紅叉分開來。因此，我們需要一個非線性決策邊界(non-linear decision boundary)來分離它們。

激活函數對于將神經網絡的輸出壓縮進特定邊界內也非常關鍵。神經元的輸出值可以非常大。該輸出在未經修改的情況下饋送至下一層神經元時，可以被轉換成更大的值，這樣過程就需要極大算力。激活函數的一個任務就是將神經元的輸出映射到有界的區域(如，0 到 1 之間)。

 

了解這些背景知識之后，我們就可以了解不同類型的激活函數了。

5. 不同類型的非線性激活函數

(1) Sigmoid

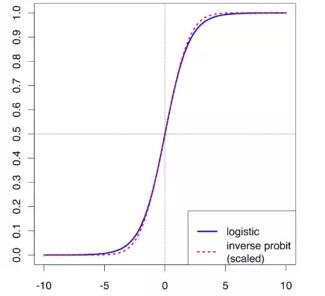
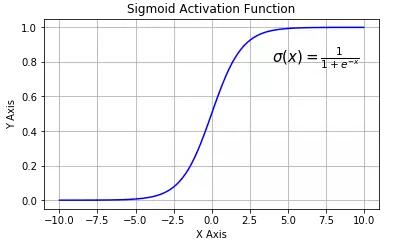
Sigmoid又叫作 Logistic 激活函數，它將實數值壓縮進 0 到 1 的區間內，還可以在預測概率的輸出層中使用。該函數將大的負數轉換成 0，將大的正數轉換成 1。數學公式為：

下圖展示了 Sigmoid 函數及其導數：

Sigmoid 激活函數

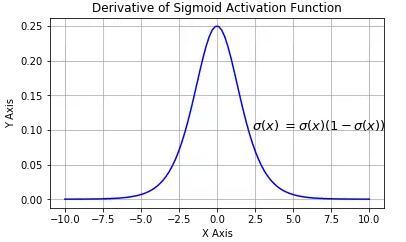
Sigmoid 導數

Sigmoid 函數的三個主要缺陷：

1. 梯度消失：注意：Sigmoid 函數趨近 0 和 1 的時候變化率會變得平坦，也就是說，Sigmoid 的梯度趨近于 0。神經網絡使用 Sigmoid 激活函數進行反向傳播時，輸出接近 0 或 1 的神經元其梯度趨近于 0。這些神經元叫作飽和神經元。因此，這些神經元的權重不會更新。此外，與此類神經元相連的神經元的權重也更新得很慢。該問題叫作梯度消失。因此，想象一下，如果一個大型神經網絡包含 Sigmoid 神經元，而其中很多個都處于飽和狀態，那么該網絡無法執行反向傳播。
2. 不以零為中心：Sigmoid 輸出不以零為中心的。
3. 計算成本高昂：exp() 函數與其他非線性激活函數相比，計算成本高昂。

下一個要討論的非線性激活函數解決了 Sigmoid 函數中值域期望不為 0 的問題。

(2) Tanh

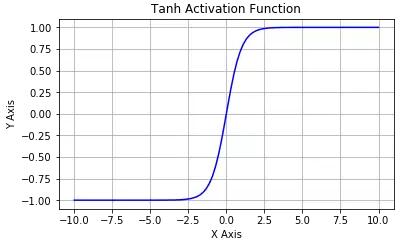
Tanh 激活函數

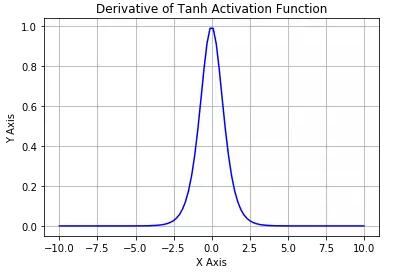
Tanh 導數

Tanh 激活函數又叫作雙曲正切激活函數(hyperbolic tangent activation function)。與 Sigmoid 函數類似，Tanh 函數也使用真值，但 Tanh 函數將其壓縮至-1 到 1 的區間內。與 Sigmoid 不同，Tanh 函數的輸出以零為中心，因為區間在-1 到 1 之間。你可以將 Tanh 函數想象成兩個 Sigmoid 函數放在一起。在實踐中，Tanh 函數的使用優先性高于 Sigmoid 函數。負數輸入被當作負值，零輸入值的映射接近零，正數輸入被當作正值。

唯一的缺點是：Tanh 函數也會有梯度消失的問題，因此在飽和時也會「殺死」梯度。

為了解決梯度消失問題，我們來討論另一個非線性激活函數——修正線性單元(rectified linear unit，ReLU)，該函數明顯優于前面兩個函數，是現在使用最廣泛的函數。

(3) 修正線性單元(ReLU)

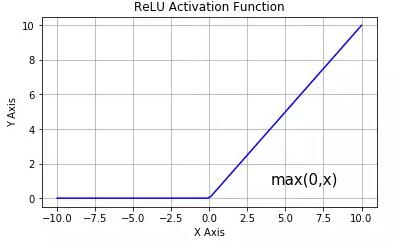
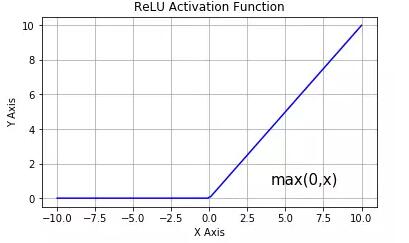
ReLU 激活函數

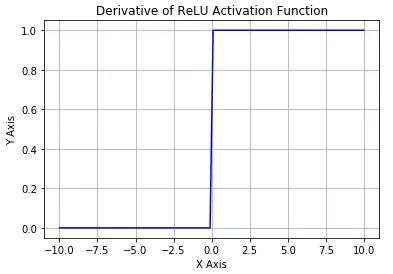
ReLU 導數

從上圖可以看到，ReLU 是從底部開始半修正的一種函數。數學公式為：

當輸入 x<0 時，輸出為 0，當 x> 0 時，輸出為 x。該激活函數使網絡更快速地收斂。它不會飽和，即它可以對抗梯度消失問題，至少在正區域(x> 0 時)可以這樣，因此神經元至少在一半區域中不會把所有零進行反向傳播。由于使用了簡單的閾值化(thresholding)，ReLU 計算效率很高。但是 ReLU 神經元也存在一些缺點：

• 不以零為中心：和 Sigmoid 激活函數類似，ReLU 函數的輸出不以零為中心。
• 前向傳導(forward pass)過程中，如果 x < 0，則神經元保持非激活狀態，且在后向傳導(backward pass)中「殺死」梯度。這樣權重無法得到更新，網絡無法學習。當 x = 0 時，該點的梯度未定義，但是這個問題在實現中得到了解決，通過采用左側或右側的梯度的方式。

為了解決 ReLU 激活函數中的梯度消失問題，當 x < 0 時，我們使用 Leaky ReLU——該函數試圖修復 dead ReLU 問題。下面我們就來詳細了解 Leaky ReLU。

(4) Leaky ReLU

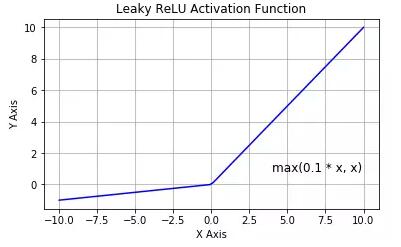
Leaky ReLU 激活函數

該函數試圖緩解 dead ReLU 問題。數學公式為：

Leaky ReLU 的概念是：當 x < 0 時，它得到 0.1 的正梯度。該函數一定程度上緩解了 dead ReLU 問題，但是使用該函數的結果并不連貫。盡管它具備 ReLU 激活函數的所有特征，如計算高效、快速收斂、在正區域內不會飽和。

Leaky ReLU 可以得到更多擴展。不讓 x 乘常數項，而是讓 x 乘超參數，這看起來比 Leaky ReLU 效果要好。該擴展就是 Parametric ReLU。

(5) Parametric ReLU

PReLU 函數的數學公式為：

其中是超參數。這里引入了一個隨機的超參數，它可以被學習，因為你可以對它進行反向傳播。這使神經元能夠選擇負區域最好的梯度，有了這種能力，它們可以變成 ReLU 或 Leaky ReLU。

 

總之，最好使用 ReLU，但是你可以使用 Leaky ReLU 或 Parametric ReLU 實驗一下，看看它們是否更適合你的問題。

(6) Swish

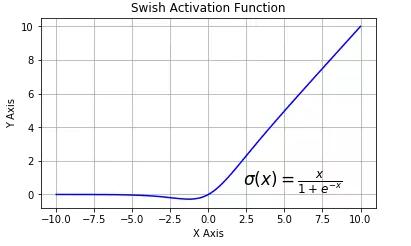
Swish 激活函數

該函數又叫作自門控激活函數，它近期由谷歌的研究者發布，數學公式為：

根據論文(https://arxiv.org/abs/1710.05941v1)，Swish 激活函數的性能優于 ReLU 函數。

根據上圖，我們可以觀察到在 x 軸的負區域曲線的形狀與 ReLU 激活函數不同，因此，Swish 激活函數的輸出可能下降，即使在輸入值增大的情況下。大多數激活函數是單調的，即輸入值增大的情況下，輸出值不可能下降。而 Swish 函數為 0 時具備單側有界(one-sided boundedness)的特性，它是平滑、非單調的。更改一行代碼再來查看它的性能，似乎也挺有意思。

原文：https://www.learnopencv.com/understanding-activation-functions-in-deep-learning/

【本文是51CTO專欄機構“機器之心”的原創譯文，微信公眾號“機器之心( id: almosthuman2014)”】

 

戳這里，看該作者更多好文