數據科學中的陷阱:定性變量的處理
在之前的文章里(《數據科學中的陷阱:變量的數學運算合理嗎?》),我們討論過定性變量,也就是表示類別的變量,比如性別、省份等。對于這類變量,不能在模型里直接使用它們,因為定性變量之間的數學計算是毫無意義的。另一方面,定性變量是一類很常見的變量,通常帶著很有價值的信息。因此,這篇文章就將討論如何正確地在模型里使用定性變量。
對于定性變量,常見的處理方法有兩種:一種是將定性變量轉換為多個虛擬變量,另一種對將有序的定性變量轉換為定量變量。
一、虛擬變量
正如前文中討論的,直接對定性變量數字編碼,得到的變量將無法進行有意義的數學運算。那么,相應的解決方法就是使得變換之后的變量不能直接做數學運算。
為了便于理解,我們先來看一個簡單的例子:使用身高和性別對體重構建線性回歸模型。性別是一個二元定性變量,可能的取值為男或女。用兩個新生成的變量來取代性別,記為(x1, x2)。其中,x1 = 1表示性別為男, x1 = 0表示性別不為男; x2類似,表示性別是否為女。在學術上,新生成的變量被稱為虛擬變量(dummy variable)。虛擬變量是一種特殊的離散型變量,可能的值只有兩個:0或1,因此也被稱為0/1變量。
用y表示體重, z表示身高,于是有:
注意到![]() ,也就是變量和變量成線性關系。這會導致另外一個問題:多重共線性(多重共線性源自線性模型,它是指由于自變量之間存在高度相關關系而使模型參數估計不準確,我們會在后面的文章里詳細討論)這個由虛擬變量引起的多重共線性問題在學術上被稱為虛擬變量陷阱(dummy variable trap)。為了規避這個問題,我們對公式(1)做如下的數學變換,得到:
,也就是變量和變量成線性關系。這會導致另外一個問題:多重共線性(多重共線性源自線性模型,它是指由于自變量之間存在高度相關關系而使模型參數估計不準確,我們會在后面的文章里詳細討論)這個由虛擬變量引起的多重共線性問題在學術上被稱為虛擬變量陷阱(dummy variable trap)。為了規避這個問題,我們對公式(1)做如下的數學變換,得到:
上面的數學轉換可翻譯為:首先選擇性別男為基準類別,生成一維虛擬變量,變量的含義與之前相同。這個變量前面的系數b - a表示性別女相對于性別男(基準類別)的體重差異。需要注意的是,針對二元定性變量,從表面上來看,直接對變量數字編碼同虛擬變量效果一樣。但這只是一個巧合而已,兩種方法有本質的區別。
將上面的方法推廣到n元定性變量(可能取值為n個的定性變量)。選擇一個類別作為基準類別,并生成n - 1個虛擬變量,分別表示剩下的n - 1個類別。在搭建模型時,用這n - 1個新生成的虛擬變量代替原來的定性變量。具體過程如圖1所示。
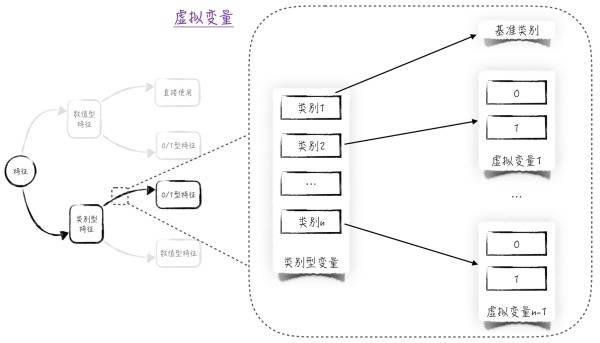
圖1二、從定性變量到定量變量
前面討論的虛擬變量的方法是比較通用的處理方法。但這種方法有一個很明顯的缺點:每個虛擬變量都是0或1,無法提供更多的信息。特別是對于多個有序的定性變量,這會損失掉每個定性變量本身的順序信息和定性變量間的關聯信息。為了解決這個問題,常常根據類別的順序,將定性變量轉換為定量變量。具體的轉換方法有很多,但限于篇幅,這里只討論其中的一種:針對二元分類問題的Ridit scoring(此方法在保險業中應用很廣),如圖2所示。
假設有序的定性變量x有t個可能的取值,記為![]() 。而且對于被預測值,排在后面的類別,y = 1發生的可能性越小。也就是說,對于y = 1這件事,其他變量相同時,類別1的概率最大,類別t的概率最小。用
。而且對于被預測值,排在后面的類別,y = 1發生的可能性越小。也就是說,對于y = 1這件事,其他變量相同時,類別1的概率最大,類別t的概率最小。用![]() 分別表示各個類別所占比例,于是類別的Ridit scoring為:
分別表示各個類別所占比例,于是類別的Ridit scoring為:
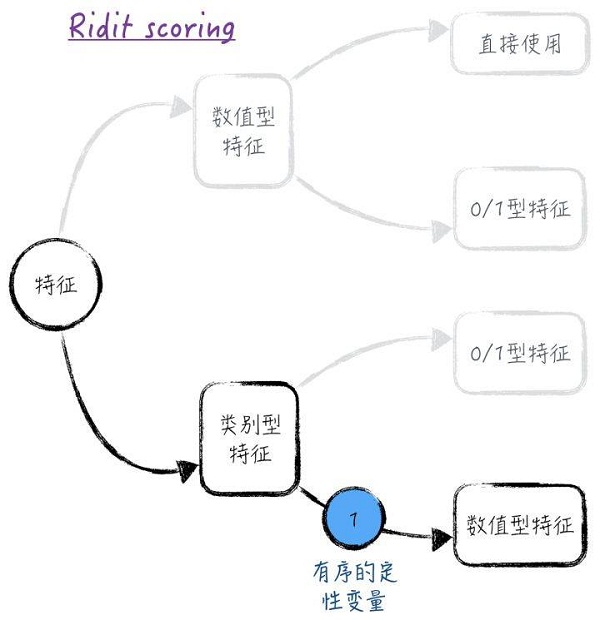
圖2對于一般的定性變量,我們也可以使用所謂的WOE(weight of evidence)方法來將其轉換為定量變量,這種方法在信貸風控領域十分廣泛。具體來說,假設二元分類問題里有兩個類別,用B和G表示(這樣標記源自金融領域,B表示bad,G表示good)。同樣假設,定性變量x有t個可能的取值,記為![]() 。那么對于取值i,它的WOE值為:
。那么對于取值i,它的WOE值為:
其中![]() 表示x等于i時,B類別的數量,
表示x等于i時,B類別的數量,![]() 表示B類別的總數量;
表示B類別的總數量;![]() 和
和![]() 表示的意思類似。
表示的意思類似。
注:這篇文章的大部分內容參考《精通數據科學:從線性回歸到深度學習》。