在機器學習中,隨著時間的推移,預測維修的話題變得越來越流行。
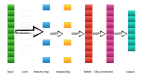
在本文中,我們將看一個分類問題。我們將使用Keras創(chuàng)建一個卷積神經(jīng)網(wǎng)絡(CNN)模型,并嘗試對結(jié)果進行直觀的解釋。
數(shù)據(jù)集
我決定從evergreen UCI repository(液壓系統(tǒng)的狀態(tài)監(jiān)測)中獲取機器學習數(shù)據(jù)集(https://archive.ics.uci.edu/ml/datasets/Condition+monitoring+of+hydraulic+systems#)。
該試驗臺由一次工作回路和二級冷卻過濾回路組成,通過油箱連接。系統(tǒng)循環(huán)重復恒定負載循環(huán)(持續(xù)時間60秒)并測量過程值,例如壓力,體積流量和溫度,同時定量地改變四個液壓元件(冷卻器、閥門、泵和蓄能器)的狀態(tài)。
我們可以想象有一個液壓管道系統(tǒng),該系統(tǒng)周期性地接收到由于管道內(nèi)某種液體的轉(zhuǎn)變而產(chǎn)生的脈沖。此現(xiàn)象持續(xù)60秒,采用不同Hz頻率的傳感器(傳感器物理量單位采樣率,PS1 Pressure bar, PS2 Pressure bar, PS3 Pressure bar, PS4 Pressure bar, PS5 Pressure bar, PS6 Pressure bar, EPS1電機功率, FS1體積流量, FS2體積流量, TS1溫度, TS2溫度, TS3溫度, TS4溫度, VS1振動, VS1振動、CE冷卻效率、CP冷卻功率、SE效率系數(shù))進行測量。
我們的目的是預測組成管道的四個液壓元件的狀況。這些目標條件值以整數(shù)值的形式注釋(易于編碼),并告訴我們每個周期特定組件是否接近失敗。
讀取數(shù)據(jù)
每個傳感器測量的值在特定的txt文件中可用,其中每一行以時間序列的形式占用一個周期。
我決定考慮來自溫度傳感器(TS1、TS2、TS3、TS4)的數(shù)據(jù),該傳感器的測量頻率為1 Hz(每一個cicle進行60次觀察)。
- label = pd.read_csv('profile.txt', sep=' ', header=None)
- data = ['TS1.txt','TS2.txt','TS3.txt','TS4.txt']
- df = pd.DataFrame()
- #read and concat data
- for txt in data:
- read_df = pd.read_csv(txt, sep=' ', header=None)
- df = df.append(read_df)
- #scale data
- def scale(df):
- return (df - df.mean(axis=0))/df.std(axis=0)
- df = df.apply(scale)
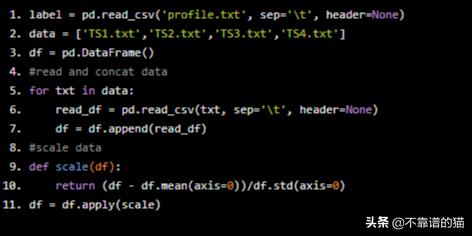
對于第一個周期,我們從溫度傳感器得到這些時間序列:
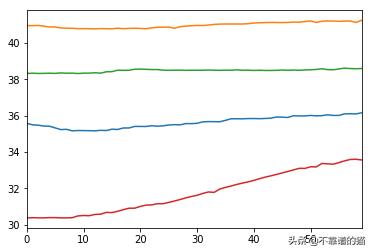
Temperature Series for cicle1 from TS1 TS2 TS3 TS4
機器學習模型
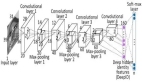
為了捕捉有趣的特征和不明顯的相關(guān)性,我們決定采用一維卷積神經(jīng)網(wǎng)絡(CNN)。這種機器學習模型非常適合對傳感器的時間序列進行分析,并強制在短的固定長度段中重塑數(shù)據(jù)。
我選擇了Keras網(wǎng)站上描述的卷積神經(jīng)網(wǎng)絡(CNN),并更新了參數(shù)。該機器學習模型的建立是為了對制冷元件的狀態(tài)進行分類,僅對給出溫度時間序列的數(shù)組形式(t_period x n_sensor for each single cycle)作為輸入。
- n_sensors, t_periods = 4, 60
- model = Sequential()
- model.add(Conv1D(100, 6, activation='relu', input_shape=(t_periods, n_sensors)))
- model.add(Conv1D(100, 6, activation='relu'))
- model.add(MaxPooling1D(3))
- model.add(Conv1D(160, 6, activation='relu'))
- model.add(Conv1D(160, 6, activation='relu'))
- model.add(GlobalAveragePooling1D())
- model.add(Dropout(0.5))
- model.add(Dense(3, activation='softmax'))
- model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
- BATCH_SIZE, EPOCHS = 16, 10
- history = model.fit(X_train, y_train, batch_size=BATCH_SIZE,
- epochs=EPOCHS, validation_split=0.2, verbose=1)
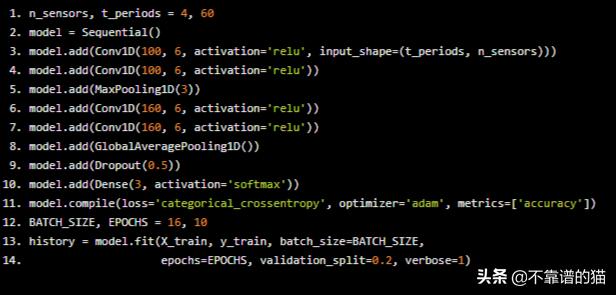
在這種情況下只有10個epochs,我們能夠取得驚人的成果!
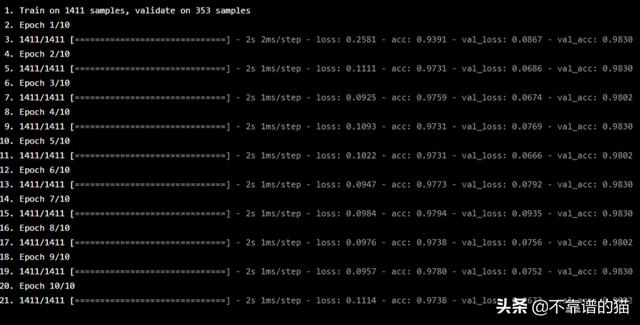
對測試數(shù)據(jù)進行預測,機器學習模型達到0.9909的準確度
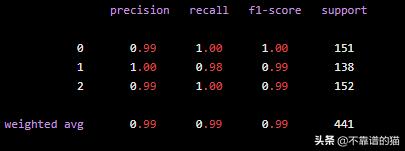
因為通過這種方式,我們能夠檢測并防止系統(tǒng)中可能出現(xiàn)的故障。
可視化結(jié)果
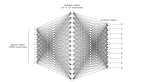
如果我們想要對系統(tǒng)狀態(tài)有一個總體的了解,那么查看圖形表示可能會很有用。為了達到這一目標,我們重新利用我們在上面構(gòu)建的卷積神經(jīng)網(wǎng)絡(CNN)來制作一個解碼器,并從每個周期的時間序列中提取特征。使用keras,這可以在一行Python代碼中實現(xiàn):
- emb_model = Model(inputs=model.input, outputs=model.get_layer('global_average_pooling1d_1').output)
新模型是一個解碼器,它接收與分類任務中使用的NN格式相同的輸入數(shù)據(jù)(t_period x n_sensor for each single cycle),并以嵌入形式返回“預測”,嵌入形式來自具有相對維數(shù)的GlobalAveragePooling1D層(每一個循環(huán)有160個嵌入變量)。
使用我們的編碼器在測試數(shù)據(jù)上計算預測,采用技術(shù)來減小尺寸(如PCA或T-SNE)并繪制結(jié)果,我們可以看到:
- tsne = TSNE(n_components=2, random_state=42, n_iter=300, perplexity=5)
- T = tsne.fit_transform(test_cycle_emb)
- fig, ax = plt.subplots(figsize=(16,9))
- colors = {0:'red', 1:'blue', 2:'yellow'}
- ax.scatter(T.T[0], T.T[1], c=[colors[i] for i in y_test])
- plt.show()
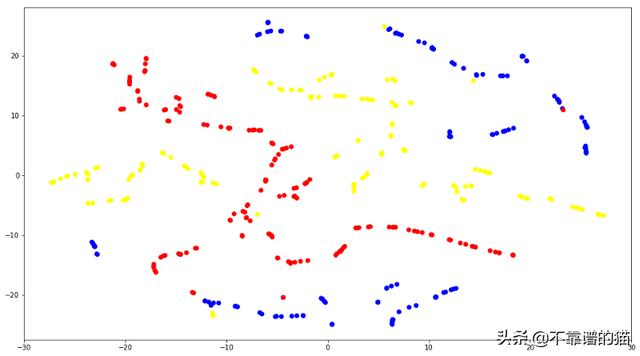
TSNE用于測試數(shù)據(jù)的循環(huán)嵌入
每個點都表示測試集中的一個循環(huán),相對顏色是Cooler條件的目標類。可以看出如何很好地定義冷卻器組件的目標值之間的區(qū)別。這種方法是我們模型性能的關(guān)鍵指標。