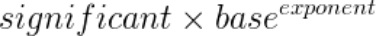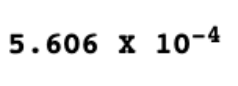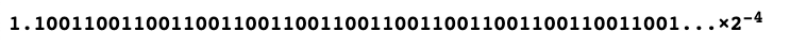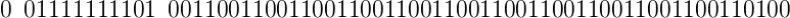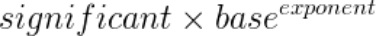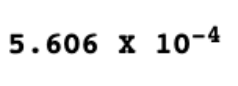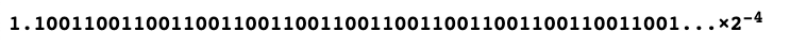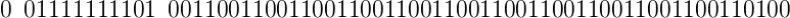打開(kāi)你的 Python,輸入「0.1+0.2=」,結(jié)果是多少?0.30000000000000004 對(duì)不對(duì)?為什么結(jié)果不是 0.3?本文作者給出了詳細(xì)的解釋。
打開(kāi)你的 Python,輸入「0.1+0.2=」,結(jié)果是多少?0.30000000000000004 對(duì)不對(duì)?為什么結(jié)果不是 0.3?本文作者給出了詳細(xì)的解釋。
從小我們就知道 0.1 + 0.2=0.3。但是,在光怪陸離的計(jì)算世界中,運(yùn)算方式卻大相徑庭。
我最近開(kāi)始用 JavaScript 進(jìn)行編碼,在閱讀數(shù)據(jù)類(lèi)型時(shí),我注意到 0.1 + 0.2 不等于 0.3 的奇怪行為。我向 Stack Overflow 尋求幫助,在上面找到了一些有用的帖子。如下圖所示:
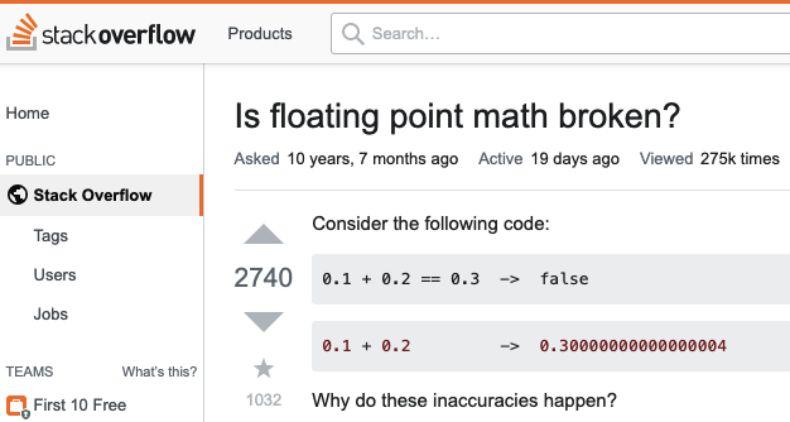
經(jīng)過(guò)大量的研究和數(shù)學(xué)運(yùn)算后,我得出結(jié)論,這不是錯(cuò)誤。這是數(shù)學(xué)運(yùn)算中的浮點(diǎn)運(yùn)算。讓我們進(jìn)一步了解內(nèi)在機(jī)制。
問(wèn)題描述: 為什么 0.1 + 0.2 = 0.30000000000000004?
如果你用 Java 或 C 語(yǔ)言編過(guò)程,那你一定知道用于存儲(chǔ)值的不同數(shù)據(jù)類(lèi)型。我們?cè)谇懊娴挠懻撝袑⒖紤]兩種數(shù)據(jù)類(lèi)型:整數(shù)型和浮點(diǎn)型。
整數(shù)型存儲(chǔ)整數(shù),而浮點(diǎn)型存儲(chǔ)小數(shù)。
在這之前,我們先來(lái)了解一個(gè)小概念:為了實(shí)現(xiàn)計(jì)算,數(shù)字是如何表示的?極小數(shù)和極大數(shù)通常用科學(xué)計(jì)數(shù)法表示,即:
同樣,如果一個(gè)用科學(xué)計(jì)數(shù)法書(shū)寫(xiě)的數(shù)字小數(shù)點(diǎn)前有一個(gè)非零的十進(jìn)制數(shù),則該數(shù)字是標(biāo)準(zhǔn)化寫(xiě)法。例如,0.0005606 用科學(xué)計(jì)數(shù)法的標(biāo)準(zhǔn)化寫(xiě)法為:
Significant 是指不包含零的有效數(shù)字,base 表示所使用的進(jìn)制——此處為十進(jìn)制(10)。Exponent(指數(shù))表示小數(shù)點(diǎn)需要向左或向右移動(dòng)的步數(shù)。
現(xiàn)在,有兩種顯示浮點(diǎn)數(shù)的方法:單精度和雙精度。在進(jìn)行浮點(diǎn)運(yùn)算時(shí),單精度使用 32 位,而雙精度使用 64 位。
與許多其他編程語(yǔ)言不同,JavaScript 并未定義不同類(lèi)型的數(shù)字?jǐn)?shù)據(jù)類(lèi)型,而是始終遵循國(guó)際 IEEE 754 標(biāo)準(zhǔn),將數(shù)字存儲(chǔ)為雙精度浮點(diǎn)數(shù)。
這種格式以 64 位存儲(chǔ)數(shù)字,其中數(shù)字(分?jǐn)?shù))存儲(chǔ)在位 0 到 51 中,指數(shù)存儲(chǔ)在位 52 到 62 中,符號(hào)存儲(chǔ)在位 63 中。
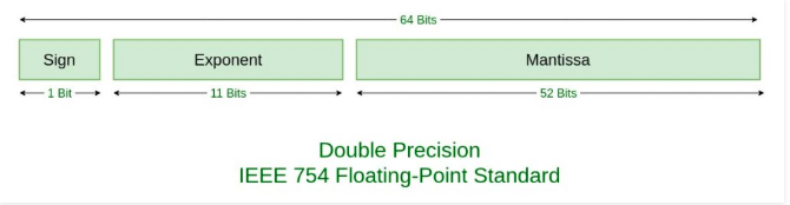
IEEE754 雙精度標(biāo)準(zhǔn)。
我們按 IEEE754 標(biāo)準(zhǔn)用 64 位表示 0.1。第一步是將十進(jìn)制的 0.1 轉(zhuǎn)換為二進(jìn)制的 0.1。首先將 0.1 乘以 2,然后將小數(shù)點(diǎn)前的數(shù)字分離出來(lái),得到其相應(yīng)的二進(jìn)制數(shù)。
重復(fù)此操作至 64 位。然后把它們按升序排列,獲取尾數(shù),再根據(jù)雙精度標(biāo)準(zhǔn),我們將把其四舍五入到 52 位。
用科學(xué)計(jì)數(shù)法表示二進(jìn)制 0.1 并只保留前 52 位:
尾數(shù)部分處理好后。現(xiàn)在我們用下面的方式處理指數(shù):
這里,11 代表我們要使用的 64 位表示的指數(shù)位數(shù),-4 代表科學(xué)計(jì)數(shù)中的指數(shù)。
轉(zhuǎn)換為浮點(diǎn)數(shù),它變成:
這就是 0.1 + 0.2 = 0.30000000000000004 的原因。