圖解堆結構、堆排序及堆的應用
前言
這次我們介紹另一種時間復雜度為 O(nlogn) 的選擇類排序方法叫做堆排序。
我將從以下幾個方面介紹:
- 堆的結構
- 堆排序
- 優化的堆排序
- 原地堆排序
- 堆的應用
堆的結構
什么是堆?我給出了百度的定義,如下:
堆(Heap)是計算機科學中一類特殊的數據結構的統稱。堆通常是一個可以被看做一棵 完全二叉樹 的數組對象。
堆總是滿足下列性質:
- 堆中某個節點的值總是不大于或不小于其父節點的值。
- 堆總是一棵完全二叉樹。
將根節點最大的堆叫做最大堆,根節點最小的堆叫做最小堆。
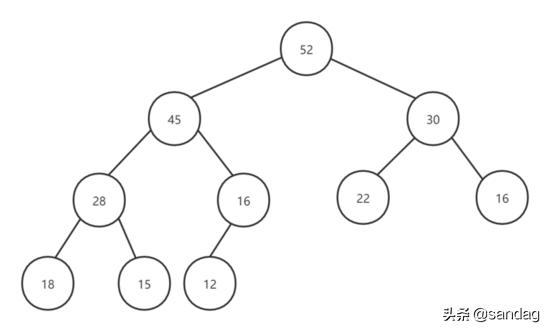
下圖展示了一個最大堆的結構:
可見,堆中某個節點的值總是小于等于其父節點的值。
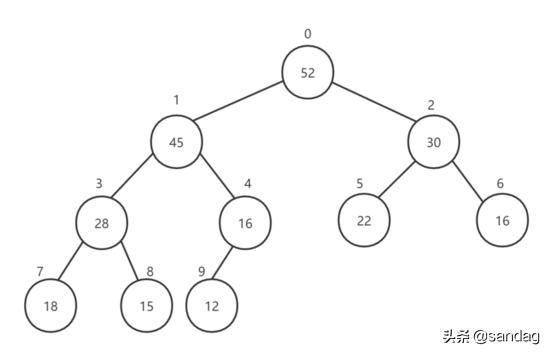
由于堆是一棵完全二叉樹,因此我們可以對每一層進行編號,如下:
我們完全可以使用數組存放這些元素,那如何確定存放的位置呢?利用如下公式:
- 父節點:parent(i) = (i-1)/2
- 左孩子:leftChild(i) = 2*i+1
- 右孩子:rightChild(i) = 2*i+2
相關代碼如下:
- private int parent(int index) {
- return (index - 1) / 2;
- }
- private int leftChild(int index) {
- return index * 2 + 1;
- }
- private int rightChild(int index) {
- return index * 2 + 2;
- }
添加元素
向堆中添加元素的步驟如下:
- 將新元素放到數組的末尾。
- 獲取新元素的父親節點在數組中的位置,比較新元素和父親節點的值,如果父親節點的值小于新元素的值,那么兩者交換。以此類推,不斷向上比較,直到根節點結束。
下圖展示了添加元素的過程:
添加元素的過程也叫做 siftUp ,代碼如下:
- // Array是自己實現的動態數組
- private Array<E> data;
- public void add(E e) {
- data.addLast(e);
- siftUp(data.getSize() - 1);
- }
- private void siftUp(int k) {
- while (k > 0 && data.get(parent(k)).compareTo(data.get(k)) < 0) {
- data.swap(k, parent(k));
- k = parent(k);
- }
- }
刪除元素
刪除元素其實就是刪除堆頂的元素,步驟如下:
- 讓數組最后一個元素和數組第一個元素(堆頂元素)交換。
- 交換完后,刪除數組最后的元素。
- 讓堆頂元素和左右孩子節點比較,如果堆頂元素比左右孩子節點中最大的元素還要大,那么滿足堆的性質,直接退出。否則如果堆頂元素比左右孩子節點中最大的元素小,那么堆頂元素就和最大的元素交換,然后繼續重復執行以上操作,只不過這時候把堆頂元素稱為父節點更好。
下圖展示了刪除元素的過程:
刪除元素的過程也叫做 siftDown ,代碼如下:
- // 這里我們不命名為remove,命名為extractMax,抽取堆頂最大元素
- public E extractMax() {
- E ret = findMax();
- // 讓最后一個葉子節點補到根節點,然后讓它下沉
- // (為什么是取最后一個葉子節點,因為即使取走最后一個葉子節點,依舊能保持是一棵完全二叉樹)
- data.swap(0, data.getSize() - 1);
- data.removeLast();
- siftDown(0);
- return ret;
- }
- private void siftDown(int k) {
- while (leftChild(k) < data.getSize()) {
- int j = leftChild(k);
- if (j + 1 < data.getSize() && data.get(j + 1).compareTo(data.get(j)) > 0) {
- j = rightChild(k);
- // data[j]是leftChild和rightChild中的最大值
- }
- // 如果父節點比左右孩子中的最大值還要大,那么說明沒有問題,直接退出
- if (data.get(k).compareTo(data.get(j)) >= 0) {
- break;
- }
- // 否則交換
- data.swap(k, j);
- k = j;
- }
- }
最大堆的完整代碼
堆排序
通過上面的介紹,我們應該明白了堆的結構,堆的添加和刪除元素操作是如何完成的。那么對于堆排序來說,就是小菜一碟了,因為堆排序就是用到了堆的添加和刪除操作,步驟如下:
- 將數組中元素一個個添加到堆(最大堆)中。
- 添加完成后,每次取出一個元素倒序放入到數組中。
堆排序代碼:
- ublic static void sort(Comparable[] arr) {
- int n = arr.length;
- // MaxHeap是自己實現的最大堆
- MaxHeap<Comparable> maxHeap = new MaxHeap<>(n);
- for (int i = 0; i < n; i++) {
- maxHeap.add(arr[i]);
- }
- for (int i = n - 1; i >= 0; i--) {
- arr[i] = maxHeap.extractMax();
- }
- }
堆排序完整代碼
優化的堆排序
在上述的堆排序中,我們在將數組中元素添加到堆時,都是一個個添加,是否有優化的方法呢?答案是有的,我們可以將數組直接轉換成堆,這種操作叫做 Heapify 。
Heapify 就是從最后一個節點開始,判斷父節點是否比孩子節點大,不是就 siftDown 。 Heapify 操作的時間復雜度是 O(n) ,相比一個個添加的時間復雜度是 O(nlogn) ,可見性能提升了不少。
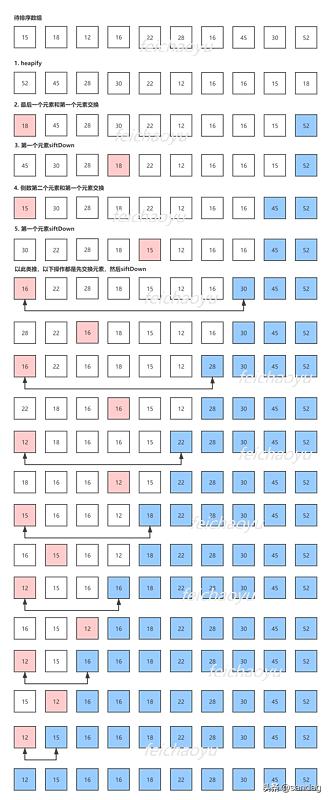
假設我們有數組: [15, 18, 12, 16, 22, 28, 16, 45, 30, 52] ,下圖展示了對其進行 Heapify 的過程。
優化的堆排序代碼:
- public static void sort(Comparable[] arr) {
- int n = arr.length;
- // MaxHeap是自己實現的最大堆,當傳入數組作為構造參數時,會對其進行heapify
- MaxHeap<Comparable> maxHeap = new MaxHeap<>(arr);
- for (int i = n - 1; i >= 0; i--) {
- arr[i] = maxHeap.extractMax();
- }
- }
- // 構造方法
- public MaxHeap(E[] arr) {
- data = new Array<>(arr);
- // 將數組堆化的過程就是從最后一個節點開始,判斷父節點是否比子節點大,不是就siftDown
- for (int i = parent(arr.length - 1); i >= 0; i--) {
- siftDown(i);
- }
- }
優化的堆排序完整代碼
原地堆排序
原地堆排序可以讓我們的空間復雜度變為 O(1) ,因為不占用新的數組。
原地堆排序類似于堆的刪除元素,步驟如下:
- Heapify
- siftDown
- siftDown
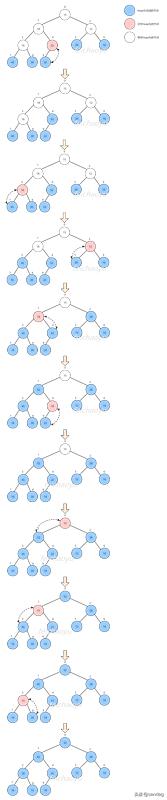
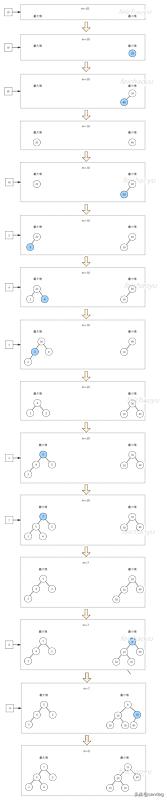
下圖展示了原地堆排序的過程:
原地堆排序代碼:
- public static void sort(Comparable[] arr) {
- int n = arr.length;
- // heapify
- for (int i = parent(n-1); i >= 0; i--) {
- siftDown(arr, n, i);
- }
- // 核心代碼
- for (int i = n - 1; i > 0; i--) {
- swap(arr, 0, i);
- siftDown(arr, i, 0);
- }
- }
- private static void swap(Object[] arr, int i, int j) {
- Object t = arr[i];
- arr[i] = arr[j];
- arr[j] = t;
- }
- private static void siftDown(Comparable[] arr, int n, int k) {
- while (leftChild(k) < n) {
- int j = leftChild(k);
- if (j + 1 < n && arr[j + 1].compareTo(arr[j]) > 0) {
- j = rightChild(k);
- }
- // 如果父節點比左右孩子中的最大值還要大,那么說明沒有問題,直接退出
- if (arr[k].compareTo(arr[j]) >= 0) {
- break;
- }
- // 否則交換
- swap(arr, k, j);
- k = j;
- }
- }
原地堆排序完整代碼
堆的應用
優先級隊列
一旦我們掌握了堆這個數據結構,那么優先級隊列的實現就很簡單了,只需要弄清楚優先級隊列需要有哪些接口就行。JDK 中自帶的 PriorityQueue 就是用堆實現的優先級隊列,不過需要注意 PriorityQueue 內部使用的是最小堆。
優先級隊列完整代碼
Top K 問題
Top K 問題就是求解 前 K 個 最大的元素或者最小的元素。元素個數不確定,數據量可能很大,甚至源源不斷到來,但需要知道目前為止前 K 個最大或最小的元素。當然問題還可能變為求解 第 K 個 最大的元素或最小的元素。
通常我們有如下解決方案:
- 使用JDK中自帶的排序,如 Arrays.sort() ,由于底層使用的快速排序,所以時間復雜度為 O(nlogn) 。但是如果 K 取值很小,比如是 1,即取最大值,那么對所有元素排序就沒有必要了。
- 使用簡單選擇排序,選擇 K 次,那么時間復雜度為 O(n*K) ,如果 K 大于 logn,那還不如快排呢!
上述兩種思路都是假定所有元素已知,如果元素個數不確定,且數據源源不斷到來的話,就無能為力了。
下面提供一種新的思路:
我們維護一個長度為 K 的數組,最前面 K 個元素就是目前最大的 K 個元素,以后每來一個新元素,都先找數組中的最小值,將新元素與最小值相比,如果小于最小值,則什么都不變,如果大于最小值,則將最小值替換為新元素。這樣一來,數組中維護的永遠是最大的 K 個元素,不管數據源有多少,需要的內存開銷都是固定的,就是長度為 K 的數組。不過,每來一個元素,都需要找到最小值,進行 K 次比較,是否有辦法能減少比較次數呢?
當然,這時候堆就要登場了,我們使用最小堆維護這 K 個元素,每次來新的元素,只需要和根節點比較,小于等于根節點,不需要變化,否則用新元素替換根節點,然后 siftDown 調整堆即可。此時的時間復雜度為 O(nlogK) ,相比上述兩種方法,效率大大提升,且空間復雜度也大大降低。
Top K 問題代碼:
- public class TopK<E extends Comparable<E>> {
- private PriorityQueue<E> p;
- private int k;
- public TopK(int k) {
- this.k = k;
- this.p = new PriorityQueue<>(k);
- }
- public void addAll(Collection<? extends E> c) {
- for (E e : c) {
- add(e);
- }
- }
- public void add(E e) {
- // 未滿k個時,直接添加
- if (p.size() < k) {
- p.add(e);
- return;
- }
- E head = p.peek();
- if (head != null && head.compareTo(e) >= 0) {
- // 小于等于TopK中的最小值,不用變
- return;
- }
- // 否則,新元素替換原來的最小值
- p.poll();
- p.add(e);
- }
- /**
- * 獲取當前的最大的K個元素
- *
- * @param a 返回類型的空數組
- * @param <T>
- * @return TopK以數組形式
- */
- public E[] toArray(E[] a) {
- return p.toArray(a);
- }
- /**
- * 獲取第K個最大的元素
- *
- * @return 第K個最大的元素
- */
- public E getKth() {
- return p.peek();
- }
- public static void main(String[] args) {
- TopK<Integer> top5 = new TopK<>(5);
- top5.addAll(Arrays.asList(88, 1, 5, 7, 28, 12, 3, 22, 20, 70));
- System.out.println("top5:" + Arrays.toString(top5.toArray(new Integer[0])));
- System.out.println("5th:" + top5.getKth());
- }
- }
這里我們直接利用 JDK 自帶的由最小堆實現的優先級隊列 PriorityQueue 。
依此思路,可以實現求前 K 個最小元素,只需要在實例化 PriorityQueue 時傳入一個反向比較器參數,然后更改 add 方法的邏輯。
中位數
堆也可以用于求解中位數,數據量可能很大且源源不斷到來。
注意:如果元素個數是偶數,那么我們假定中位數取任意一個都可以。
有了上面的例子,這里就很好理解了。我們使用兩個堆,一個最大堆,一個最小堆,步驟如下:
- 添加的第一個元素作為中位數 m,最大堆維護 <= m 的元素,最小堆維護 >= m 的元素,兩個堆都不包含 m。
- 當添加第二個元素 e 時,將 e 與 m 比較,若 e <= m,則將其加入到最大堆中,否則加入到最小堆中。
- 如果出現最小堆和最大堆的元素個數相差 >= 2,則將 m 加入元素個數少的堆中,然后讓元素個數多的堆將根節點移除并賦值給 m。
- 以此類推不斷更新。
假設有數組 [20, 30, 40, 50, 2, 4, 3, 5, 7, 8, 10] 。
下圖展示了整個操作的過程:
求解中位數的代碼:
- public class Median<E extends Comparable<E>> {
- /**
- * 最小堆
- */
- private PriorityQueue<E> minP;
- /**
- * 最大堆
- */
- private PriorityQueue<E> maxP;
- /**
- * 當前中位數
- */
- private E m;
- public Median() {
- this.minP = new PriorityQueue<>();
- this.maxP = new PriorityQueue<>(11, Collections.reverseOrder());
- }
- private int compare(E e, E m) {
- return e.compareTo(m);
- }
- public void addAll(Collection<? extends E> c) {
- for (E e : c) {
- add(e);
- }
- }
- public void add(E e) {
- // 第一個元素
- if (m == null) {
- m = e;
- return;
- }
- if (compare(e, m) <= 0) {
- // 小于等于中值,加入最大堆
- maxP.add(e);
- } else {
- // 大于中值,加入最大堆
- minP.add(e);
- }
- if (minP.size() - maxP.size() >= 2) {
- // 最小堆元素個數多,即大于中值的數多
- // 將 m 加入到最大堆中,然后將最小堆中的根移除賦給 m
- maxP.add(m);
- m = minP.poll();
- } else if (maxP.size() - minP.size() >= 2) {
- minP.add(m);
- m = maxP.poll();
- }
- }
- public E getMedian() {
- return m;
- }
- public static void main(String[] args) {
- Median<Integer> median = new Median<>();
- median.addAll(Arrays.asList(20, 30, 40, 50, 2, 4, 3, 5, 7, 8, 10));
- System.out.println(median.getMedian());
- }
- }