本文主要分享基于python的數據分析三方庫pandas，numpy的一次爬坑經歷，發現并分析了python語言對于浮點數精度處理不準確的問題，并在最后給出合理的解決方案。如果你也在用python處理數據，建議看一下，畢竟0.1的誤差都可能造成比較大的影響。

問題出現

早上到了公司，領導發了幾個文件過來，說這兩天測試環境跑出來的數據，與實際情況有所出入，看看哪出的問題，盡快解決···

開始排查

• 先對比數據，發現并不是所有的數據都出現問題，只有10%左右的數據有這個問題，說明應該不是邏輯上的問題，初步判斷可能為個別情況需要特殊處理，考慮不周導致
• 檢查梳理各個運算模塊，用debug斷點調試一波，確定了數據出現偏差的模塊
• 通過單獨測試這個單元模塊最終確定，涉及到兩數相除結果為0.5(浮點數)的地方有問題
• 預期結果：np.round(0.5)=1，實際運算結果：np.round(0.5)=0，于是我做了如下的試驗

# 基于python3.7版本 
>>> import numpy as np 
 
# 先看看 0 < x < 1 這個范圍的結果，發現有問題 
>>> np.round(0.50) 
0.0 
>>> np.round(0.51) 
1.0 
>>> np.round(0.49) 
0.0 
 
# 我擔心是不是只有小數點為.5的都會呈現這種問題,所以測試了 x > 1的結果，發現還是有問題 
>>> np.round(1.5) 
2.0 
>>> np.round(2.5) 
2.0 
>>> np.round(3.5) 
4.0 
>>> np.round(4.5) 
4.0 

通過對比，發現確實涉及到.5的值會有些和預想的不同，看看啥原因

分析問題

確實發現了關于浮點數(.5出現了理解上的偏差)，看看官方文檔怎么解釋這個現象

numpy.around(a, decimals=0, out=None)[source] 
Evenly round to the given number of decimals. 
 
# 對于恰好介于四舍五入的十進制值之間的中間值(.5)，NumPy會四舍五入為最接近的偶數值。  
# 因此1.5和2.5四舍五入為2.0，-0.5和0.5四舍五入為0.0，依此類推。 
For values exactly halfway between rounded decimal values,  
NumPy rounds to the nearest even value.  
Thus 1.5 and 2.5 round to 2.0, -0.5 and 0.5 round to 0.0, etc. 
 
# np.around使用快速但有時不精確的算法來舍入浮點數據類型。 
# 對于正小數，它等效于np.true_divide（np.rint（a * 10 **小數），10 **小數）， 
# 由于IEEE浮點標準[1]和 十次方縮放時引入的錯誤 
np.around uses a fast but sometimes inexact algorithm to round floating-point datatypes.  
For positive decimals it is equivalent to np.true_divide(np.rint(a * 10**decimals), 10**decimals),  
which has error due to the inexact representation of decimal fractions in the IEEE floating point standard [1]  
and errors introduced when scaling by powers of ten 

• 其實也就是說：對于帶有.5這種剛好介于中間的值，返回的是相鄰的偶數值
• 白話解釋：如果一個數字帶有浮點數(.5)，整數部分為偶數，則返回這個偶數;整數部分奇數，則返回這個奇數+1的偶數
• 規律解釋：如果整數部分能夠整除2，則返回整數部分;如果整數部分不能整除2，則返回整數部分 +1

解決問題

先不做任何改動，看下數據誤差的情形

# 我們為了先看下現象,構造如下案例 
import pandas as pd 
import numpy as np 
 
df = pd.DataFrame({"num1": [1, 1, 1.5, 5, 7.5], "num2": [2, 3, 1, 6, 3]}) 
 
df["真實值"] = df["num1"] / df["num2"] 
# 看下round函數過后的結果 
df["偏差值"] = np.round(df["num1"] / df["num2"]) 

原始結果圖片如下

不做處理，期望值和偏差值不等的情況出現

我的解決方案

• 我根據我的精度要求，構建精度范圍所需要保留的小數點的最后一位，通過這個數字是否為5，判斷是否需要向上取整
• 舉例來說，本案例中我只需要保留整數部分的數據，那么我只需要確定小數點后第一位是否是數字5就可以了

上代碼

import pandas as pd 
import numpy as np 
import math 
 
df = pd.DataFrame({"除數": [1, 1, 1.5, 5, 7.5], "被除數": [2, 3, 1, 6, 3]}) 
 
# 記錄真實值 
df["真實值"] = df["除數"] / df["被除數"] 
 
# 記錄整數部分 
df["輔助整數列"] = df["真實值"].apply(lambda x: math.modf(x)[1]) 
 
# 記錄小數部分,因為我的最后結果精度為只保留整數部分,所以我只需要保留一個小數點位進行判斷是否需要進位操作 
df["輔助小數列"] = df["真實值"].apply(lambda x: str(math.modf(x)[0]).split(".")[1][0]) 
 
# 小數點后的第一位是為5，則向上取整，不是5則調用原np.round就行了 
df["期望值修正"] = df.apply(lambda x: x.輔助整數列 + 1 if (x.輔助小數列 == "5") else np.round(x.真實值), axis=1) 

結果如下所示

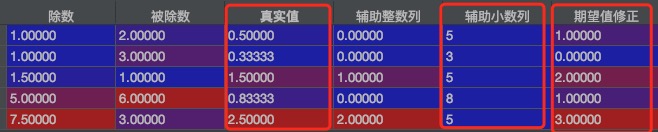
期望修正值已經達成