分析深度學習背后的數學思想
深度神經網絡(DNN)本質上是通過具有多個連接的感知器而形成的,其中感知器是單個神經元。可以將人工神經網絡(ANN)視為一個系統,其中包含沿加權路徑饋入的一組輸入。然后處理這些輸入,并產生輸出以執行某些任務。隨著時間的流逝,ANN“學習”了,并且開發了不同的路徑。各種路徑可能具有不同的權重,并且在模型中,比那些產生較少的理想結果的路徑,以及被發現更重要(或產生更理想的結果)的路徑分配了更高的權重。
在DNN中,如果所有輸入都密集連接到所有輸出,則這些層稱為密集層。此外,DNN可以包含多個隱藏層。隱藏層基本上是神經網絡輸入和輸出之間的點,激活函數對輸入的信息進行轉換。之所以稱其為隱藏層,是因為無法從系統的輸入和輸出中直接觀察到這一點。神經網絡越深,網絡可以從數據中識別的越多,輸出的信息越多。
但是,盡管目標是從數據中盡可能多地學習,但是深度學習模型可能會遭受過度擬合的困擾。當模型從訓練數據(包括隨機噪聲)中學習太多時,就會發生這種情況。然后,模型可以確定數據中非常復雜的模式,但這會對新數據的性能產生負面影響。訓練數據中拾取的噪聲不適用于新數據或看不見的數據,并且該模型無法概括發現的模式。非線性模型在深度學習模型中也非常重要,盡管該模型將從具有多個隱藏層的內容中學到很多東西,但是將線性形式應用于非線性問題將導致性能下降。
現在的問題是,“這些層如何學習東西?” 好吧,我們可以在這里將ANN應用于實際場景以解決問題并了解如何訓練模型以實現其目標。案例分析如下:
在當前的大流行中,許多學校已經過渡到虛擬學習,這使一些學生擔心他們通過課程的機會。“我將通過本課程”這個問題是任何人工智能系統都應該能夠解決的問題。
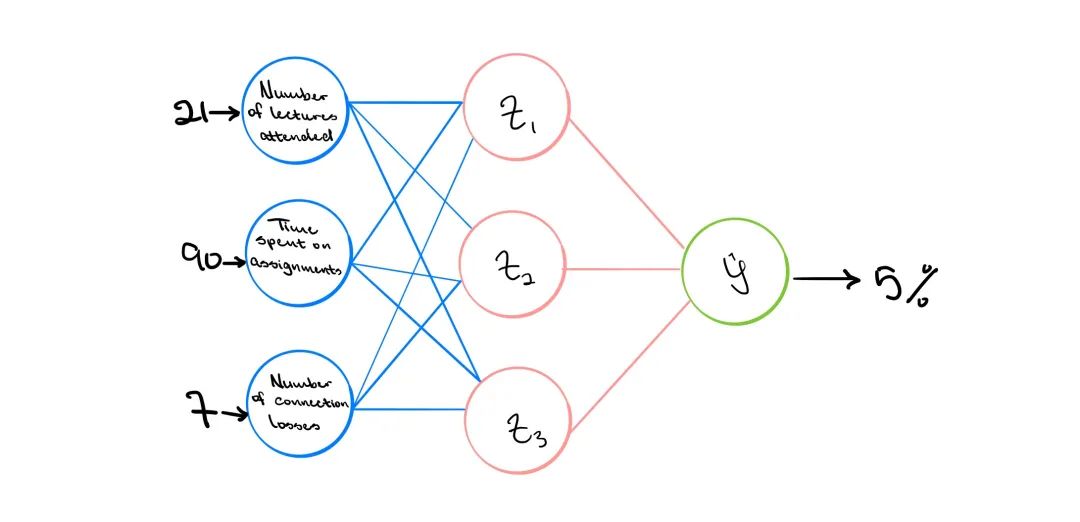
為簡單起見,讓我們考慮該模型只有3個輸入:學生參加的講座的數量,在作業上花費的時間以及整個講座中互聯網連接丟失的次數。該模型的輸出將是二進制分類。學生要么通過了課程,要么沒有通過,其實就是0和1。現在到了學期期末,學生A參加了21堂課,花了90個小時進行作業,并且在整個學期中有7次失去互聯網連接。這些輸入信息被輸入到模型中,并且輸出預測學生有5%的機會通過課程。一周后,發布了最終成績,學生A通過了該課程。那么,模型的預測出了什么問題?
從技術上講,沒有任何問題。該模型本來可以按目前開發的方式工作。問題在于該模型不知道發生了什么。我們將在路徑上初始化一些權重,但是該模型當前不知道對與錯。因此,權重不正確。這就是學習的主要源頭,其中的想法是模型需要掌握錯誤的時間的規律,我們通過計算某種形式的“損失”來做到這一點。計算得出的損失取決于當前的問題,但是通常會涉及使預測輸出與實際輸出之間的差異最小化。
在上述情況下,只有一名學生和一個錯誤點可以減少到最小。但是,通常不是這種情況。現在,如果考慮將多個學生和多個差異最小化,那,總損失通常將計算為所有預測和實際觀察值之間的差異的平均值。
回想一下,正在計算的損失取決于當前的問題。因此,由于我們當前的問題是二元分類(0和1分類),因此適當的損失計算將是交叉熵損失,該功能背后的想法是,它比較學生是否將通過課程的預測分布與實際分布,并嘗試最小化這些分布之間的差異。
取而代之的是,我們不再希望預測學生是否會通過該課程,而是希望預測他們將在該課程中獲得的分數。因此,交叉熵損失將不再是一種合適的方法。相反,均方誤差損失將更合適。此方法適用于回歸問題,其思想是將嘗試最小化實際值和預測值之間的平方差。
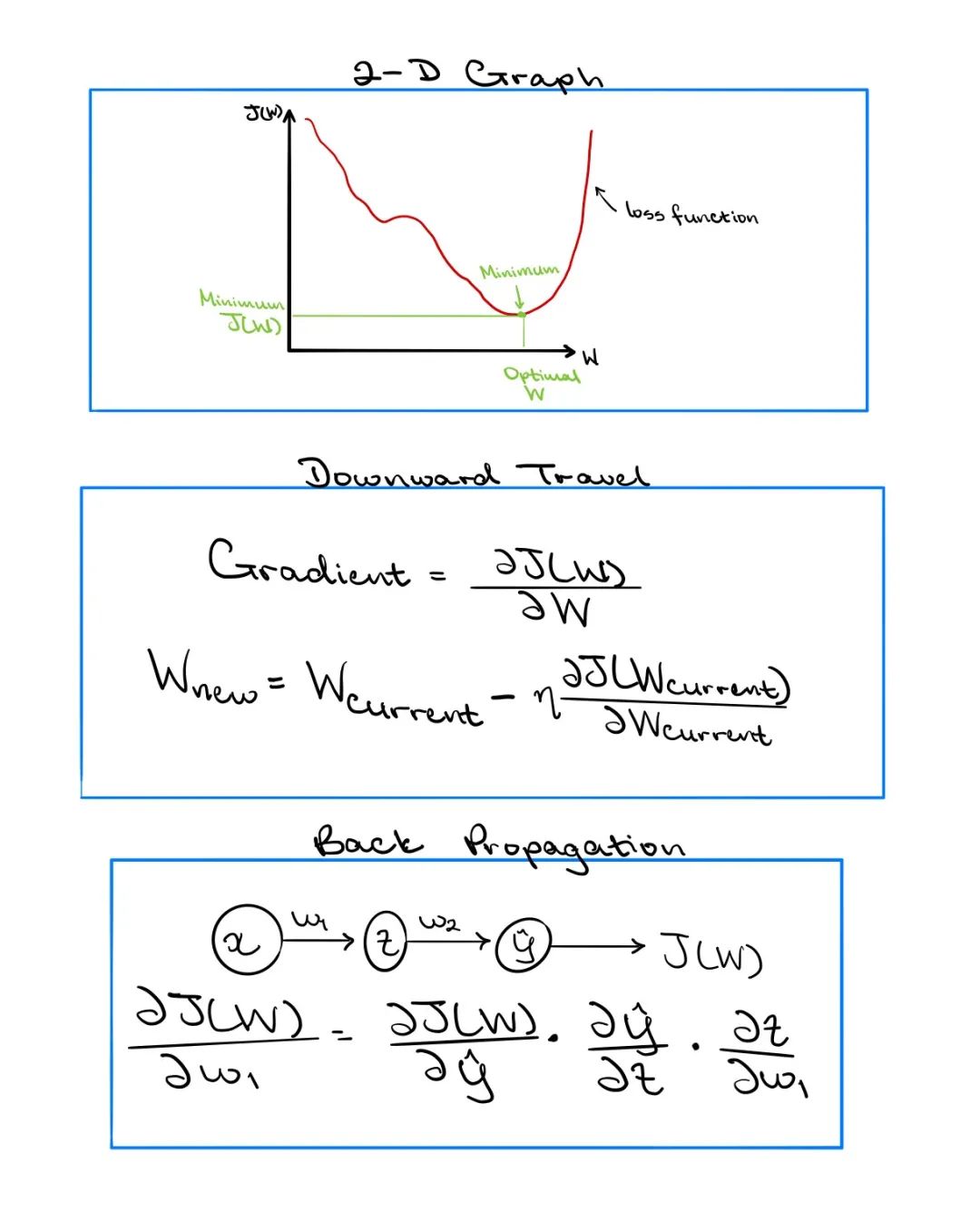
現在我們了解了一些損失函數(這里有損失函數的介紹:深度學習基礎:數學分析基礎與Tensorflow2.0回歸模型 文章末尾可下載PDF書籍),我們可以進行損失優化和模型訓練。擁有良好DNN的關鍵因素是擁有適當的權重。損耗優化應嘗試找到一組權重W,以最小化計算出的損耗。如果只有一個重量分量,則可以在二維圖上繪制重量和損耗,然后選擇使損耗最小的重量。但是,大多數DNN具有多個權重分量,并且可視化n維圖非常困難。
取而代之的是,針對所有權重計算損失函數的導數,以確定最大上升的方向。現在,模型可以理解向上和向下的方向,然后向下移動,直到達到局部最小值的收斂點。完成這一體面操作后,將返回一組最佳權重,這就是DNN應該使用的權重(假設模型開發良好的話)。
計算此導數的過程稱為反向傳播,它本質上是來自微積分的鏈式法則。考慮上面顯示的神經網絡,第一組權重的微小變化如何影響最終損失?這就是導數或梯度試圖解釋的內容。但是,第一組權重被饋送到隱藏層,然后隱藏層又具有另一組權重,從而導致預測的輸出和損失。因此,還應考慮權重變化對隱藏層的影響。現在,這些是網絡中僅有的兩個部分。但是,如果要考慮的權重更多,則可以通過應用從輸出到輸入的鏈式規則來繼續此過程。
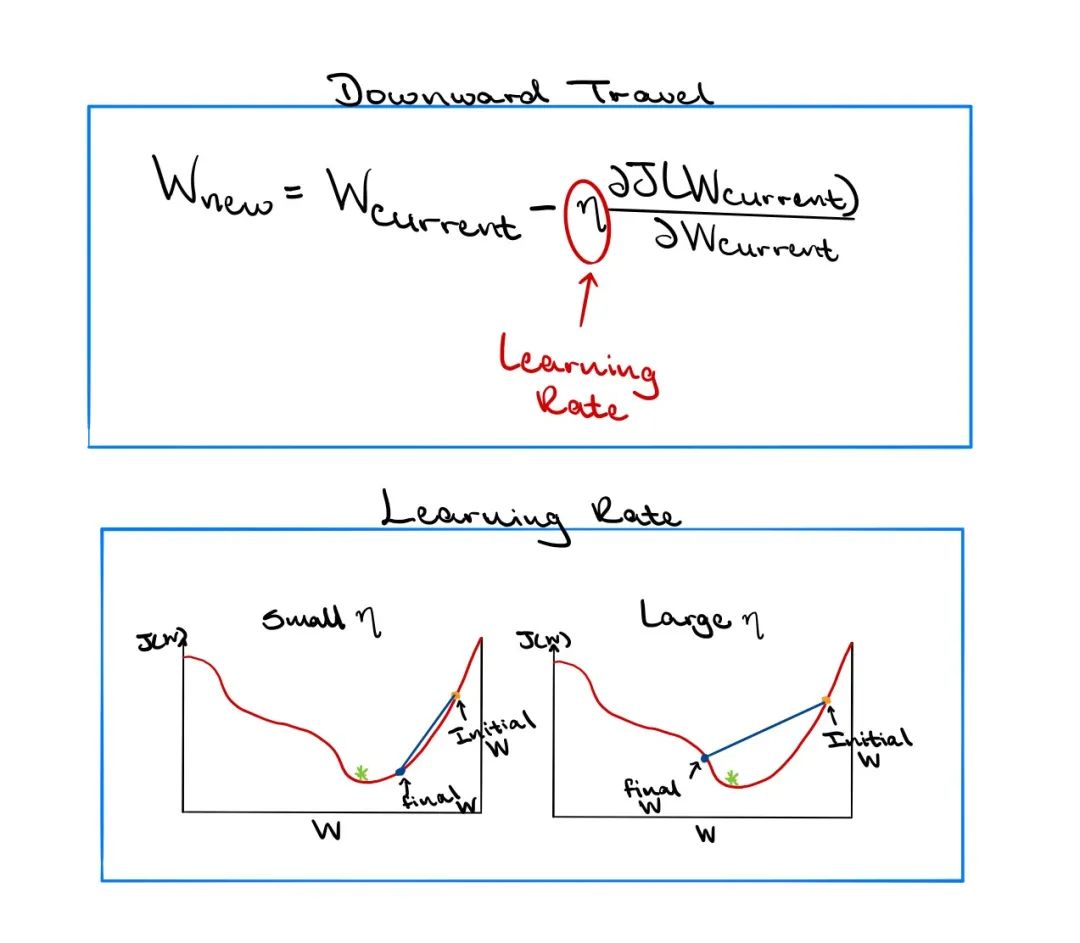
訓練DNN時要考慮的另一個重要因素是學習率(可以看做是數學中的收斂因子)。當模型行進以找到最佳的權重集時,它需要以某種因素來更新其權重。盡管這似乎微不足道,但是確定模型移動的因素非常非常必要。如果因子太小,則該模型可以運行一段指數級的長時間,也可以陷入非全局最小值的某個位置。如果因數太大,則模型可能會完全錯過目標點,然后發散。
盡管固定比率可能是理想的,但自適應學習比率會減少前面提到的問題的機會。也就是說,該系數將根據當前梯度,當前權重的大小或其他可能影響模型下一步來尋找最佳權重的地方而變化。
可以看出,DNN是基于微積分和一些統計數據構建的。評估這些深度技術過程背后的數學思想是有用的,因為它可以幫助人們了解模型中真正發生的事情,并且可以導致整體上開發出更好的模型。