成人免费xxxxx在线视频软件_久久精品久久久_亚洲国产精品久久久_天天色天天色_亚洲人成一区_欧美一级欧美三级在线观看

數據結構與算法：圖形結構

作者：Gofy
大數據 算法
圖形結構是一種比樹形結構更復雜的非線性結構。在樹形結構中，結點間具有分支層次關系，每一層上的結點只能和上一層中的至多一個結點相關，但可能和下一層的多個結點相關。而在圖形結構中，任意兩個結點之間都可能相關，即結點之間的鄰接關系可以是任意的。

圖

圖形結構是一種比樹形結構更復雜的非線性結構。在樹形結構中，結點間具有分支層次關系，每一層上的結點只能和上一層中的至多一個結點相關，但可能和下一層的多個結點相關。而在圖形結構中，任意兩個結點之間都可能相關，即結點之間的鄰接關系可以是任意的。

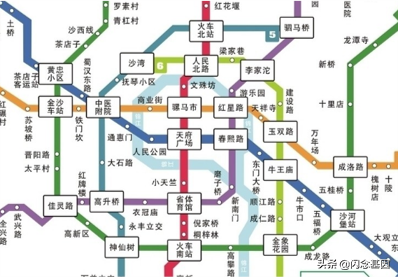
因此，圖形結構被用于描述各種復雜的數據對象，在自然科學、社會科學和人文科學等許多領域有著非常廣泛的應用 。圖形結構在計算機科學、人工智能、電子線路分析、最短路徑尋找、工程計劃、化學化合物分析統計力學、遺傳學、控制論語言學和社會科學等方面均有不同程度的應用可以這樣說，圖形結構在所有數據結構中應用最為廣泛。如在地鐵站中的線路圖：

 

數據結構與算法：圖形結構

圖的定義

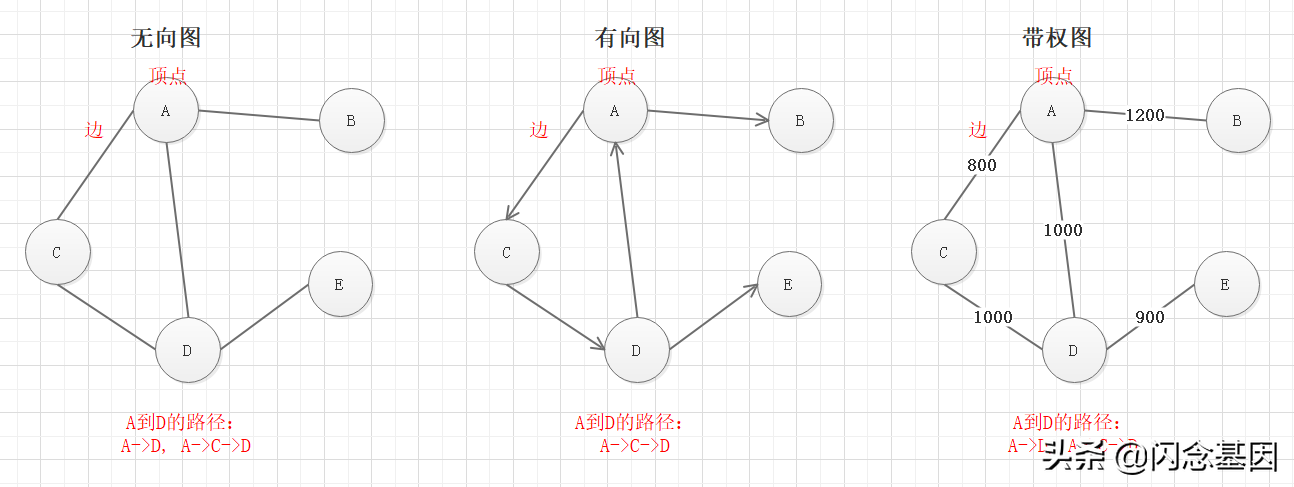
圖是一種數據結構，其中節點可以具有零個或多個相鄰元素，兩個節點的連接稱之為邊，節點在圖形結構中也被稱為頂點，一個頂點到另一個頂點的經過的的線路稱為路徑。

  • 圖形結構有3種類型：無向圖、有向圖、帶權圖
  • 無向圖：頂點A與頂點B之間的邊是無方向的，可以從A到B，也可以從B到A
  • 有向圖：頂點A與頂點B之間的邊是有方向的，可以從A到B，但不可以從B到A
  • 帶權圖：頂點A與頂點B之間的邊是帶有屬性的，如A到B的 距離。

 

數據結構與算法：圖形結構

圖的表達方式

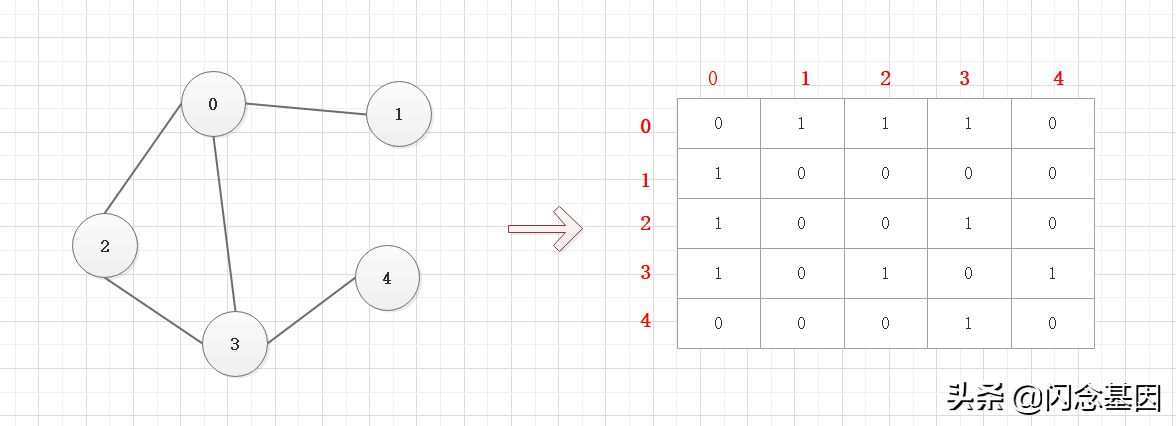
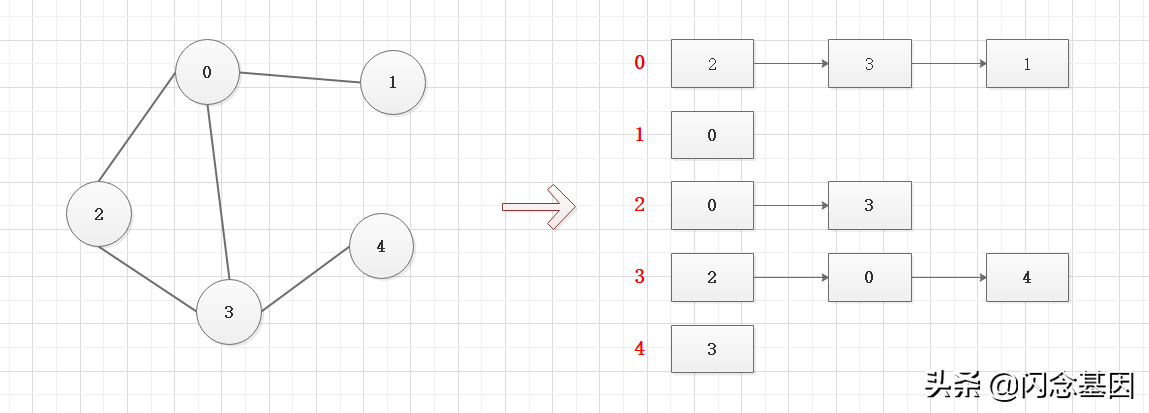
圖的表達方式有兩種：鄰接矩陣(使用二維數組)和鄰接表(使用數組+鏈表)

鄰接矩陣

鄰接矩陣是表示圖形中各頂點之間的關系，矩陣的行和列對應各頂點，坐標位置上的值對于它們之間的關系，1為連接, 0為沒有連接。在程序中用二維數組來實現。

 

數據結構與算法：圖形結構

鄰接表

鄰接表只關系存在的邊，不需要去為不存在的邊分配空間，因此比鄰接矩陣來說，避免了不必要的空間浪費。在程序中用數組+鏈表的形式實現，數組存儲對應的頂點，鏈表存儲該頂點連接的所有頂點。

 

數據結構與算法：圖形結構

圖的搜索算法

圖形結構基礎屬性和方法

以下的代碼演示都是以鄰接矩陣表達方式來實現的

 

  1. //圖形結構(鄰接矩陣) 
  2. class Graph { 
  3.      //存儲圖中所有頂點 
  4.     private List<String> vertexes; 
  5.     //圖形結構的鄰接矩陣 
  6.     private int[][] matrix; 
  7.     //各頂點訪問情況，true為已訪問，false為未訪問 
  8.     private boolean[] visited; 
  9.  
  10.     /** 
  11.      * 根據傳入的頂點信息生成矩陣 
  12.      * @param s 
  13.      */ 
  14.     public Graph(String s[]) { 
  15.         vertexes = new ArrayList<>(); 
  16.         for (String vertex : s){ 
  17.             vertexes.add(vertex); 
  18.         } 
  19.         matrix = new int[s.length][s.length]; 
  20.     } 
  21.  
  22.     /** 
  23.      * 將倆個頂點連接，即生成邊 
  24.      * @param index1 頂點在集合中的索引 
  25.      * @param index2 
  26.      */ 
  27.     public void connect(int index1, int index2){ 
  28.         if (index1 < 0 || index1 > matrix.length || index2 < 0 || index2 > matrix.length){ 
  29.             throw new RuntimeException("該頂點未存在"); 
  30.         } 
  31.         //將新的鄰接添加的鄰接矩陣中 
  32.         matrix[index1][index2] = 1; 
  33.         matrix[index2][index1] = 1; 
  34.     } 
  35.  
  36.     /** 
  37.      * 展示鄰接矩陣 
  38.      */ 
  39.     public void showGraphMatrix(){ 
  40.         for (int arr[] : matrix){ 
  41.             System.out.println(Arrays.toString(arr)); 
  42.         } 
  43.     } 
  44.      
  45.     /** 
  46.      * 獲取頂點在鄰接矩陣對應行row中的第一個鄰接頂點下標 
  47.      * @param row 
  48.      * @return 當有鄰接頂點時返回鄰接頂點下標，沒有則返回-1 
  49.      */ 
  50.     public int getFirstNeighbor(int row){ 
  51.         for(int i =0; i<matrix.length; i++){ 
  52.             if (matrix[row][i] != 0){ 
  53.                 return i; 
  54.             } 
  55.         } 
  56.         return -1; 
  57.     } 
  58.  
  59.     /** 
  60.      * 獲取頂點在鄰接矩陣對于行row中col列的下一個鄰接頂點 
  61.      * @param row 
  62.      * @param col 
  63.      * @return 當有鄰接頂點時返回鄰接頂點下標，沒有則返回-1 
  64.      */ 
  65.     public int getNeighbor(int row, int col){ 
  66.         for (int i=col+1; i<matrix.length; i++){ 
  67.             if (matrix[row][i] != 0){ 
  68.                 return i; 
  69.             } 
  70.         } 
  71.         return -1; 
  72.     } 
  73. } 

深度優先搜索

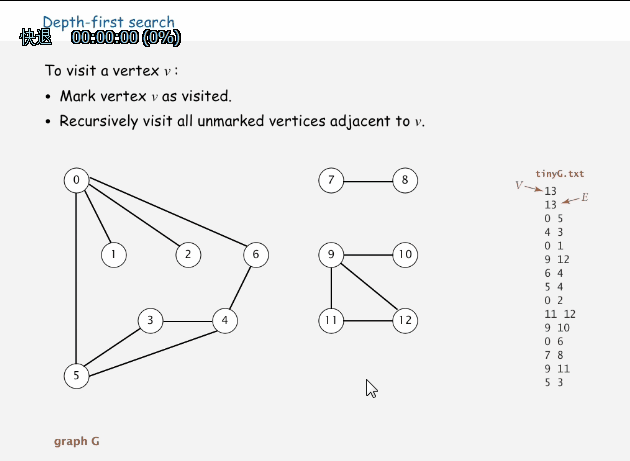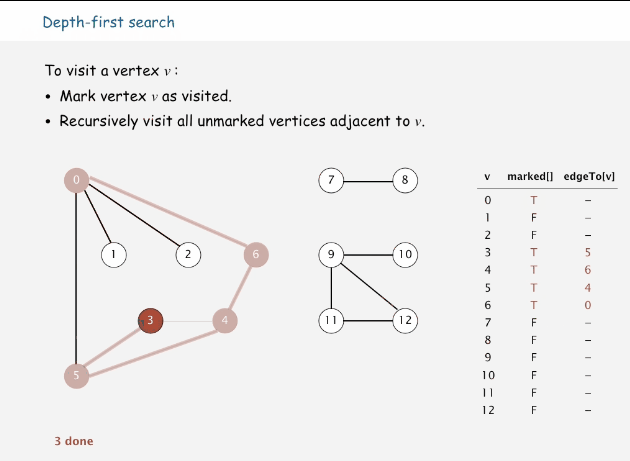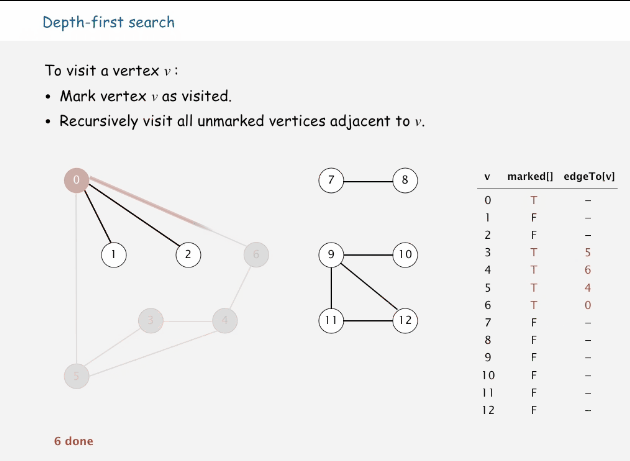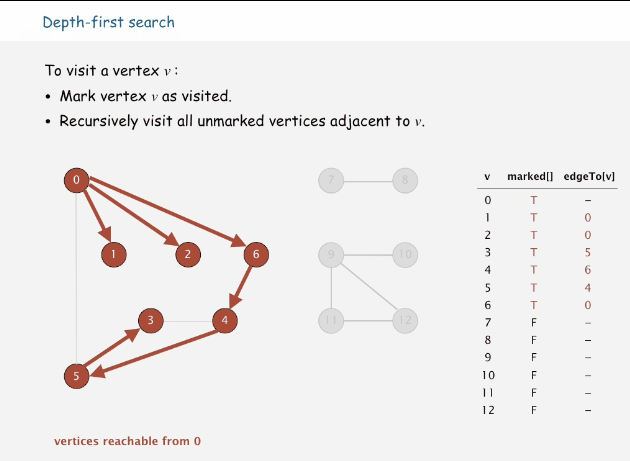
深度優先搜索屬于圖算法的一種，英文縮寫為DFS即Depth First Search.其過程簡要來說是對每一個可能的分支路徑深入到不能再深入為止，而且每個節點只能訪問一次。這樣的訪問策略是優先往縱向進行深入挖掘，而不是對一個頂點的所有鄰接頂點進行橫線訪問。簡單來說就是一條路走到死，不行再掉頭。

思路：從當前頂點選一個與之連接而未訪問過的頂點，將當前節點往該鄰接頂點移動，如果鄰接頂點沒有未訪問的，則回溯到上一個頂點位置，繼續該步驟。直到所有頂點都訪問過。

往鄰接但未訪問過的頂點移動

 

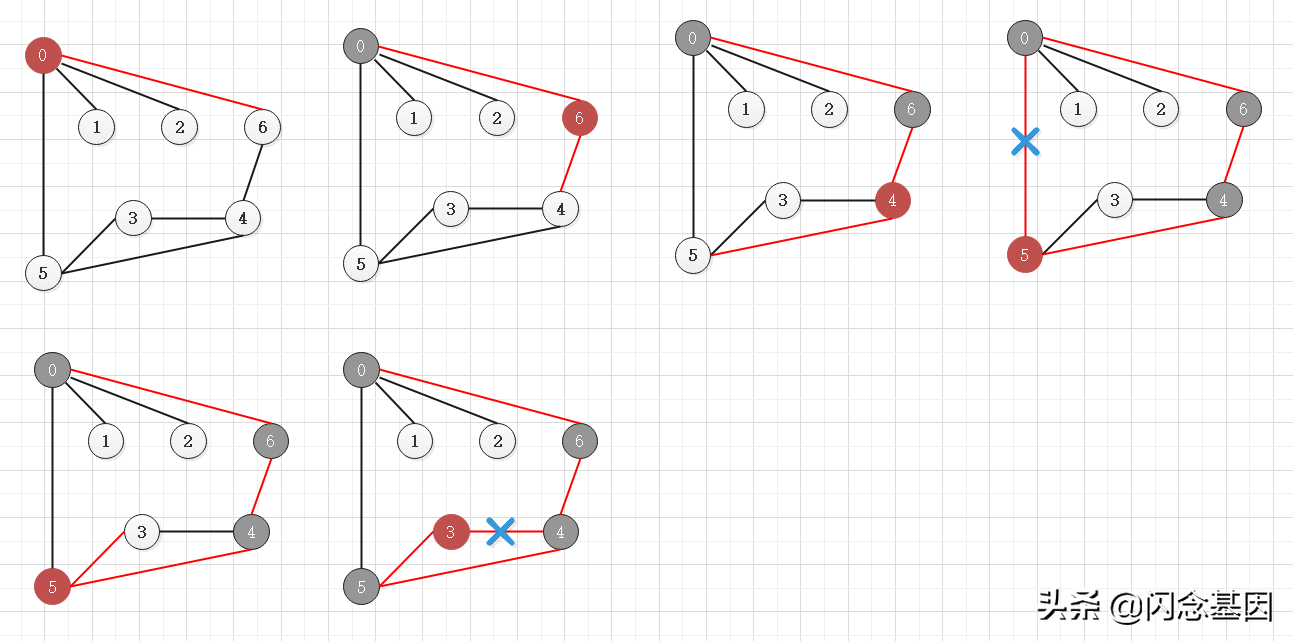
數據結構與算法：圖形結構

鄰接頂點沒有未訪問的，進行回溯，直到遇到未訪問的鄰接頂點

 

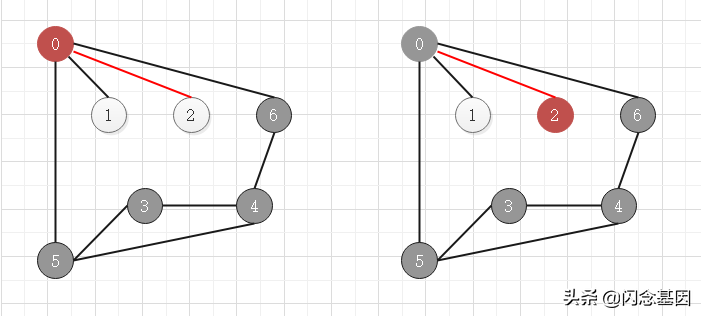
數據結構與算法：圖形結構

當所有頂點都被訪問過時，退出算法

 

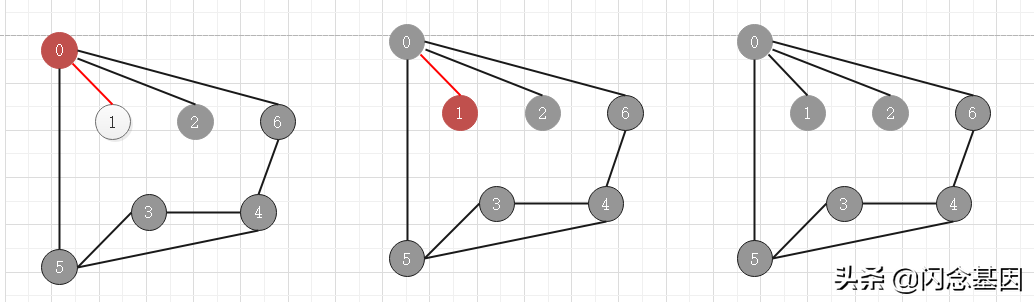
數據結構與算法：圖形結構

下面是深度優先搜索的過程動畫

 

數據結構與算法：圖形結構

代碼演示

 

  1. public void dsf(){ 
  2.     visited = new boolean[vertexes.size()]; 
  3.     //以在集合中下標為0的頂點，進行深度搜索 
  4.     dsf(visited, 0); 
  5. } 
  6.  
  7. /** 
  8.  * 深度優先搜索 
  9.  * @param visited 
  10.  * @param row 
  11.  */ 
  12. public void dsf(boolean[] visited, int row){ 
  13.     //輸出當前頂點 
  14.     System.out.print(vertexes.get(row) + " -> "); 
  15.     //將當前頂點設為已訪問 
  16.     visited[row] = true; 
  17.     //獲取當前頂點的鄰接頂點下標 
  18.     int index = getFirstNeighbor(row); 
  19.     //如果當前頂點有鄰接頂點則進行深度搜索 
  20.     while (index != -1){ 
  21.         //當鄰接頂點未訪問時，則遞歸遍歷 
  22.         if (visited[index] != true){ 
  23.             dsf(visited, index); 
  24.         } 
  25.         //當鄰接頂點已訪問時，則尋找另一個鄰接頂點 
  26.         index = getNeighbor(row, index); 
  27.     } 
  28. } 

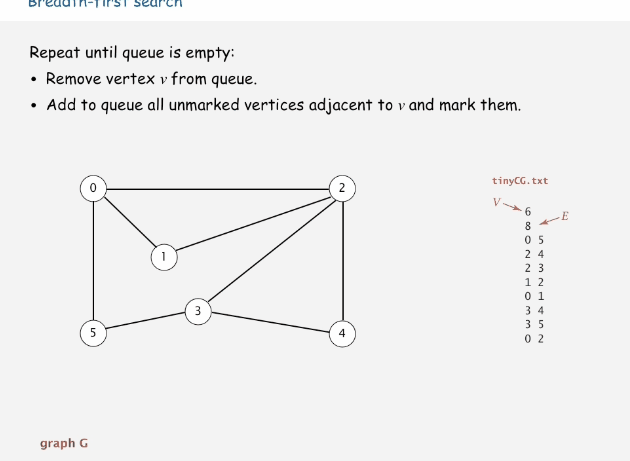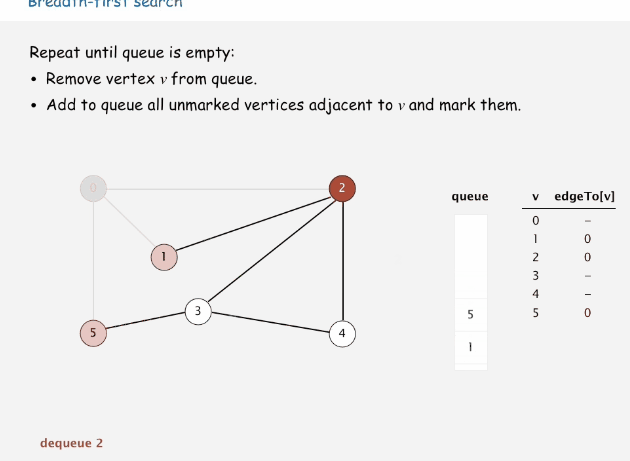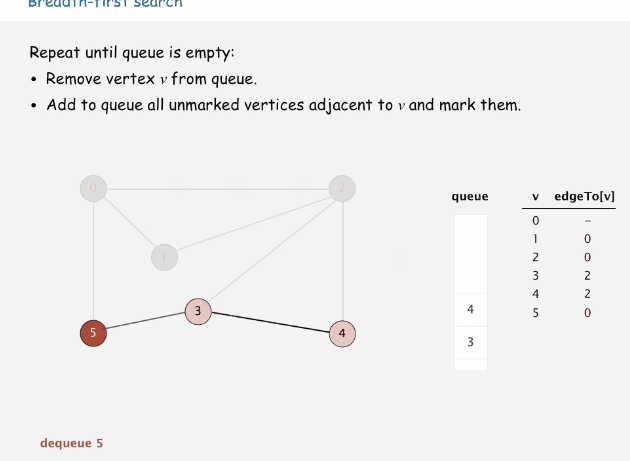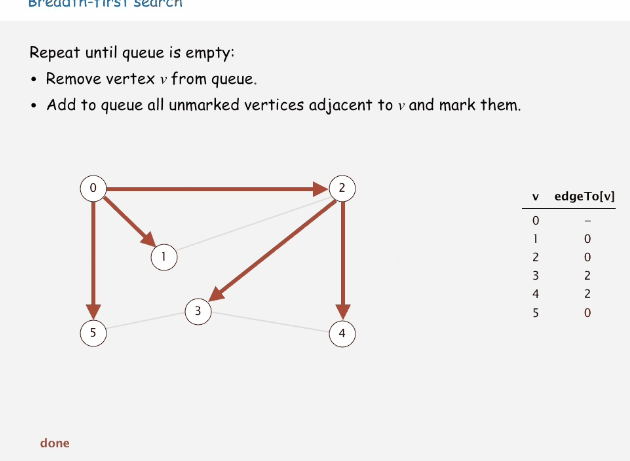
寬度優先搜索

寬度優先搜索算法(又稱廣度優先搜索)是最簡便的圖的搜索算法之一，這一算法也是很多重要的圖的算法的原型。Dijkstra單源最短路徑算法和Prim最小生成樹算法都采用了和寬度優先搜索類似的思想。其別名又叫BFS，屬于一種盲目搜尋法，目的是系統地展開并檢查圖中的所有節點，以找尋結果。換句話說，它并不考慮結果的可能位置，徹底地搜索整張圖，直到找到結果為止。

寬度優先搜索算法類似于一個分層搜索的過程，寬度優先搜索算法需要一個隊列以保持訪問過頂點的順序，以便按這個順序來訪問這些頂點的鄰接頂點。

思路：依次訪問當前頂點的鄰接頂點，并按訪問順序將這些鄰接頂點存儲在隊列中，當當前頂點的所有鄰接頂點都被訪問后，從隊列中彈出一個頂點，以該頂點為當前頂點繼續該步驟，直到所有頂點都被訪問過。

依次訪問當前頂點的所有鄰接頂點，并把這些鄰接頂點按訪問順序存儲在隊列中

 

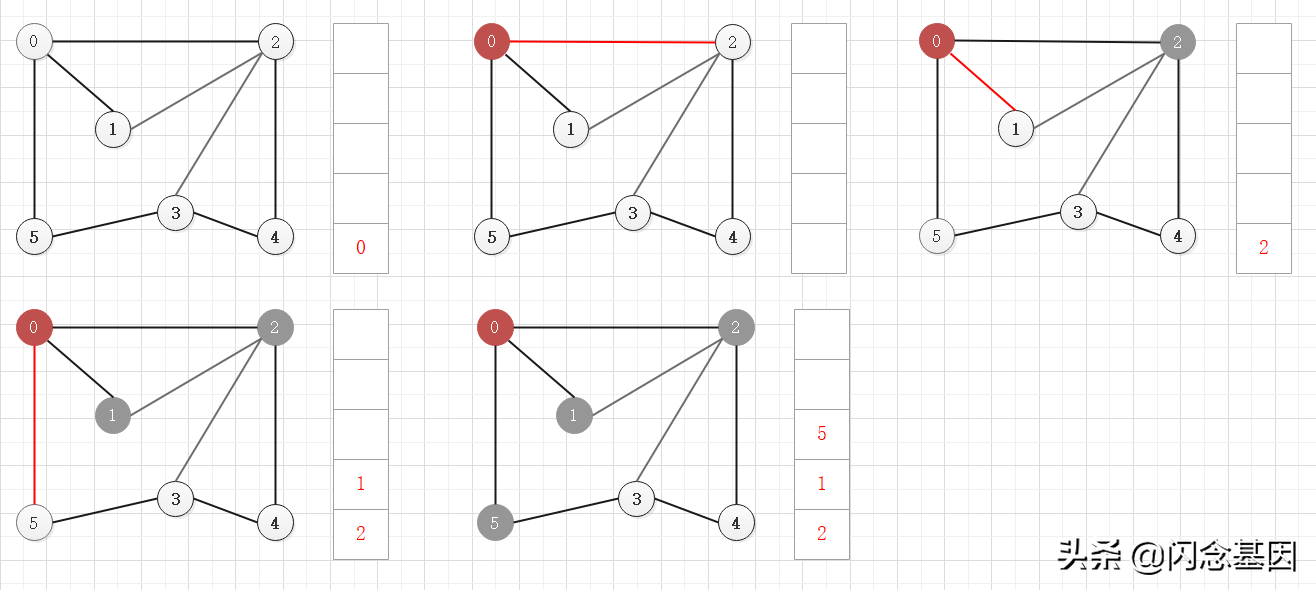
數據結構與算法：圖形結構

當前頂點沒有未訪問的鄰接頂點，從隊列中彈出一個頂點，以該彈出頂點繼續訪問未訪問的鄰接頂點

 

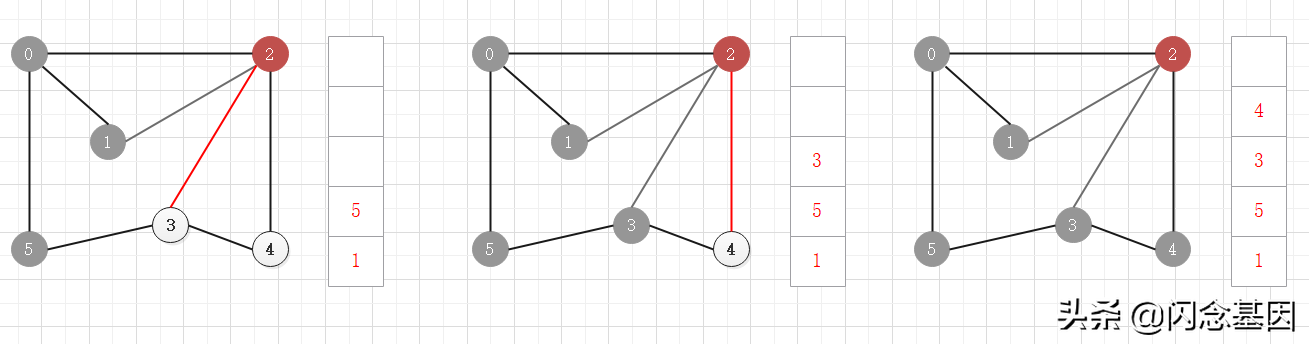
數據結構與算法：圖形結構

注意，雖然圖中的頂點都已經訪問過了，但還是要等隊列中的所有頂點彈出訪問后，算法才結束

 

數據結構與算法：圖形結構

下面時寬度優先搜索的過程動畫

 

數據結構與算法：圖形結構

代碼演示

 

  1. public void bfs(){ 
  2.     visited = new boolean[vertexes.size()]; 
  3.     ////以在集合中下標為0的頂點，進行廣度優先搜索 
  4.     bfs(visited, 0); 
  5. } 
  6.  
  7. /** 
  8.  * 廣度優先搜索 
  9.  * @param visited 
  10.  * @param row 
  11.  */ 
  12. public void bfs(boolean[] visited, int row){ 
  13.     //創建隊列，存儲遍歷鄰接頂點的順序 
  14.     LinkedList queue = new LinkedList(); 
  15.     //輸出當前頂點 
  16.     System.out.print(vertexes.get(row) + " -> "); 
  17.     //將當前頂點設為已訪問 
  18.     visited[row] = true; 
  19.     //將當前頂點加入隊列中 
  20.     queue.add(row); 
  21.     //當隊列不為空時，即有未搜索的鄰接頂點，進行搜索 
  22.     while (!queue.isEmpty()){ 
  23.         //按順序從隊列中彈出鄰接頂點下標 
  24.         int last = (Integer)queue.removeFirst(); 
  25.         //獲取該彈出頂點的鄰接頂點下標 
  26.         int index = getFirstNeighbor(last); 
  27.         //當彈出頂點有鄰接頂點時，進行廣度搜索 
  28.         while(index != -1){ 
  29.             //當鄰接頂點未訪問時 
  30.             if(visited[index] != true){ 
  31.                 //輸出該鄰接頂點 
  32.                 System.out.print(vertexes.get(index) + " -> "); 
  33.                 //把該鄰接頂點設為已訪問 
  34.                 visited[index] = true; 
  35.                 //將該鄰接頂點加入隊列 
  36.                 queue.addLast(index); 
  37.             } 
  38.             //繼續尋找彈出頂點的另一個鄰接頂點 
  39.             index = getNeighbor(last, index); 
  40.         } 
  41.     } 
  42. } 

完整演示代碼

 

  1. public class GraphDemo { 
  2.     public static void main(String[] args) { 
  3.         String[] s = {"A","B","C","D","E","F","G"}; 
  4.         Graph graph = new Graph(s); 
  5.         //A-B A-C A-G A-F F-D F-E D-E E-G 
  6.         graph.connect(0, 1); 
  7.         graph.connect(0, 2); 
  8.         graph.connect(0, 6); 
  9.         graph.connect(0, 5); 
  10.         graph.connect(5, 3); 
  11.         graph.connect(5, 4); 
  12.         graph.connect(3, 4); 
  13.         graph.connect(4, 6); 
  14.         graph.showGraphMatrix(); 
  15.  
  16.         graph.dsf();//A -> B -> C -> F -> D -> E -> G ->  
  17.         System.out.println(); 
  18.         graph.bfs();//A -> B -> C -> F -> G -> D -> E ->  
  19.     } 
  20. } 
  21.  
  22. //圖形結構 
  23. class Graph { 
  24.     //存儲圖中所有頂點 
  25.     private List<String> vertexes; 
  26.     //圖形結構的鄰接矩陣 
  27.     private int[][] matrix; 
  28.     //各頂點訪問情況，true為已訪問，false為未訪問 
  29.     private boolean[] visited; 
  30.  
  31.     /** 
  32.      * 根據傳入的頂點信息生成矩陣 
  33.      * @param s 
  34.      */ 
  35.     public Graph(String s[]) { 
  36.         vertexes = new ArrayList<>(); 
  37.         for (String vertex : s){ 
  38.             vertexes.add(vertex); 
  39.         } 
  40.         matrix = new int[s.length][s.length]; 
  41.     } 
  42.  
  43.     /** 
  44.      * 將倆個頂點連接，即生成邊 
  45.      * @param index1 頂點在集合中的索引 
  46.      * @param index2 
  47.      */ 
  48.     public void connect(int index1, int index2){ 
  49.         if (index1 < 0 || index1 > matrix.length || index2 < 0 || index2 > matrix.length){ 
  50.             throw new RuntimeException("該頂點未存在"); 
  51.         } 
  52.         //將新的鄰接添加的鄰接矩陣中 
  53.         matrix[index1][index2] = 1; 
  54.         matrix[index2][index1] = 1; 
  55.     } 
  56.  
  57.     /** 
  58.      * 展示鄰接矩陣 
  59.      */ 
  60.     public void showGraphMatrix(){ 
  61.         for (int arr[] : matrix){ 
  62.             System.out.println(Arrays.toString(arr)); 
  63.         } 
  64.     } 
  65.  
  66.     public void dsf(){ 
  67.         visited = new boolean[vertexes.size()]; 
  68.         //以在集合中下標為0的頂點，進行深度優先搜索 
  69.         dsf(visited, 0); 
  70.     } 
  71.  
  72.     /** 
  73.      * 深度優先搜索 
  74.      * @param visited 
  75.      * @param row 
  76.      */ 
  77.     public void dsf(boolean[] visited, int row){ 
  78.         //輸出當前頂點 
  79.         System.out.print(vertexes.get(row) + " -> "); 
  80.         //將當前頂點設為已訪問 
  81.         visited[row] = true; 
  82.         //獲取當前頂點的鄰接頂點下標 
  83.         int index = getFirstNeighbor(row); 
  84.         //如果當前頂點有鄰接頂點則進行深度搜索 
  85.         while (index != -1){ 
  86.             //當鄰接頂點未訪問時，則遞歸遍歷 
  87.             if (visited[index] != true){ 
  88.                 dsf(visited, index); 
  89.             } 
  90.             //當鄰接頂點已訪問時，則尋找另一個鄰接頂點 
  91.             index = getNeighbor(row, index); 
  92.         } 
  93.     } 
  94.  
  95.     public void bfs(){ 
  96.         visited = new boolean[vertexes.size()]; 
  97.         ////以在集合中下標為0的頂點，進行廣度優先搜索 
  98.         bfs(visited, 0); 
  99.     } 
  100.  
  101.     /** 
  102.      * 廣度優先搜索 
  103.      * @param visited 
  104.      * @param row 
  105.      */ 
  106.     public void bfs(boolean[] visited, int row){ 
  107.         //創建隊列，存儲遍歷鄰接頂點的順序 
  108.         Queue queue = new ArrayDeque(); 
  109.         //輸出當前頂點 
  110.         System.out.print(vertexes.get(row) + " -> "); 
  111.         //將當前頂點設為已訪問 
  112.         visited[row] = true; 
  113.         //將當前頂點加入隊列中 
  114.         queue.add(row); 
  115.         //當隊列不為空時，即有未搜索的鄰接頂點，進行搜索 
  116.         while (!queue.isEmpty()){ 
  117.             //按順序從隊列中彈出鄰接頂點下標 
  118.             int last = (Integer)queue.poll(); 
  119.             //獲取該彈出頂點的鄰接頂點下標 
  120.             int index = getFirstNeighbor(last); 
  121.             //當彈出頂點有鄰接頂點時，進行廣度搜索 
  122.             while(index != -1){ 
  123.                 //當鄰接頂點未訪問時 
  124.                 if(visited[index] != true){ 
  125.                     //輸出該鄰接頂點 
  126.                     System.out.print(vertexes.get(index) + " -> "); 
  127.                     //把該鄰接頂點設為已訪問 
  128.                     visited[index] = true; 
  129.                     //將該鄰接頂點加入隊列 
  130.                     queue.add(index); 
  131.                 } 
  132.                 //繼續尋找彈出頂點的另一個鄰接頂點 
  133.                 index = getNeighbor(last, index); 
  134.             } 
  135.         } 
  136.     } 
  137.  
  138.     /** 
  139.      * 獲取頂點在鄰接矩陣對應行row中的第一個鄰接頂點下標 
  140.      * @param row 
  141.      * @return 當有鄰接頂點時返回鄰接頂點下標，沒有則返回-1 
  142.      */ 
  143.     public int getFirstNeighbor(int row){ 
  144.         for(int i =0; i<matrix.length; i++){ 
  145.             if (matrix[row][i] != 0){ 
  146.                 return i; 
  147.             } 
  148.         } 
  149.         return -1; 
  150.     } 
  151.  
  152.     /** 
  153.      * 獲取頂點在鄰接矩陣對于行row中col列的下一個鄰接頂點 
  154.      * @param row 
  155.      * @param col 
  156.      * @return 當有鄰接頂點時返回鄰接頂點下標，沒有則返回-1 
  157.      */ 
  158.     public int getNeighbor(int row, int col){ 
  159.         for (int i=col+1; i<matrix.length; i++){ 
  160.             if (matrix[row][i] != 0){ 
  161.                 return i; 
  162.             } 
  163.         } 
  164.         return -1; 
  165.     } 
  166. } 

 

責任編輯：未麗燕 來源： Gofy的博客
數據結構算法圖形
相關推薦

2023-03-08 08:03:09

數據結構算法歸并排序

2023-10-27 07:04:20

2023-03-07 08:02:07

數據結構算法數列

2023-03-10 08:07:39

數據結構算法計數排序

2023-03-02 08:15:13

2023-04-27 09:13:20

排序算法數據結構

2023-02-08 07:52:36

跳躍表數據結構

2023-10-30 08:31:42

數據結構算法

2023-03-13 10:08:31

數據結構算法

2023-11-06 06:43:23

單鏈表查詢數據結構

2017-08-31 09:45:43

JavaArrayList數據

2023-09-15 10:33:41

算法數據結構

2021-05-12 09:07:09

Java數據結構算法

2023-09-25 12:23:18

棧Python

2020-10-30 09:56:59

Trie樹之美

2021-03-09 06:30:32

JAVA數據結構算法

2021-03-18 08:44:20

Java數據結構算法

2022-09-21 07:57:33

二叉搜索樹排序二叉樹

2021-04-13 09:37:41

Java數據結構算法

2022-09-26 07:56:53

AVL算法二叉樹
點贊
收藏

51CTO技術棧公眾號

主站蜘蛛池模板： 日韩一区二区三区在线观看视频 | 欧美做暖暖视频 | 高清欧美性猛交 | 粉嫩国产精品一区二区在线观看 | 久久久久久一区 | 中文在线一区二区 | 色婷婷精品久久二区二区蜜臂av | 久久激情av | 亚州精品天堂中文字幕 | aa级毛片毛片免费观看久 | 亚洲欧美视频 | 中文字幕 欧美 日韩 | 亚洲精品一区国语对白 | 久久国产精品一区二区 | 天天躁日日躁狠狠的躁天龙影院 | 在线观看成年视频 | 国产午夜av片 | 久草网在线视频 | 中文字幕第十一页 | 久久久久久久97 | 国产乱一区二区三区视频 | 亚洲视频在线观看免费 | 精品国产精品一区二区夜夜嗨 | 日韩成人精品视频 | 免费播放一级片 | 成人av影院 | 国产精久久久久久久 | 国产91九色 | 一本一道久久a久久精品蜜桃 | 九九热这里只有精品6 | 色综久久 | 亚洲成人一区 | 亚洲综合成人网 | 国产一区黄色 | 欧美在线高清 | 99精品视频免费观看 | 国产99精品| 亚洲综合视频 | 日韩欧美在线视频 | a级大片免费观看 | 日韩有码一区二区三区 |