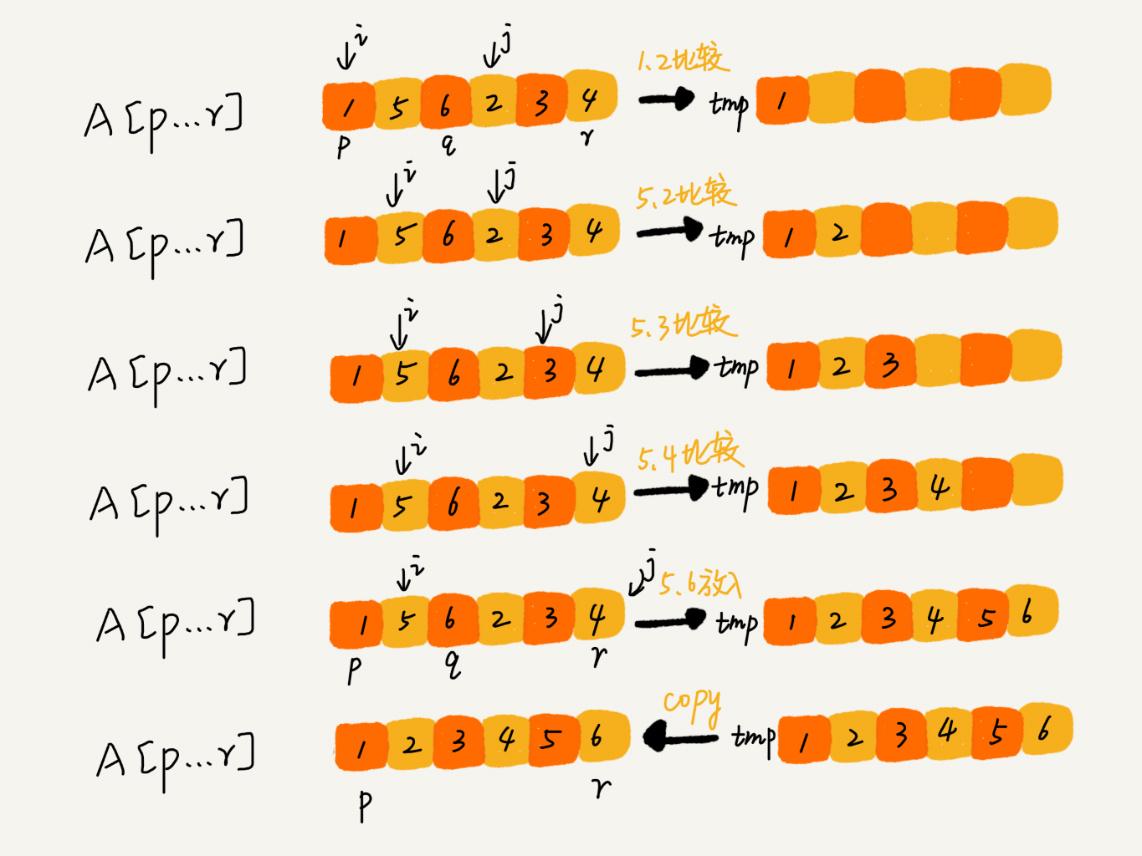一、分治思想
分治,就是分而治之,將一個大問題分解成小的子問題來解決。小的子問題解決了,大問題也就解決了。
分治算法一般都是用遞歸來實現的。分治是一種解決問題的處理思想,遞歸是一種編程技巧。
二、歸并排序
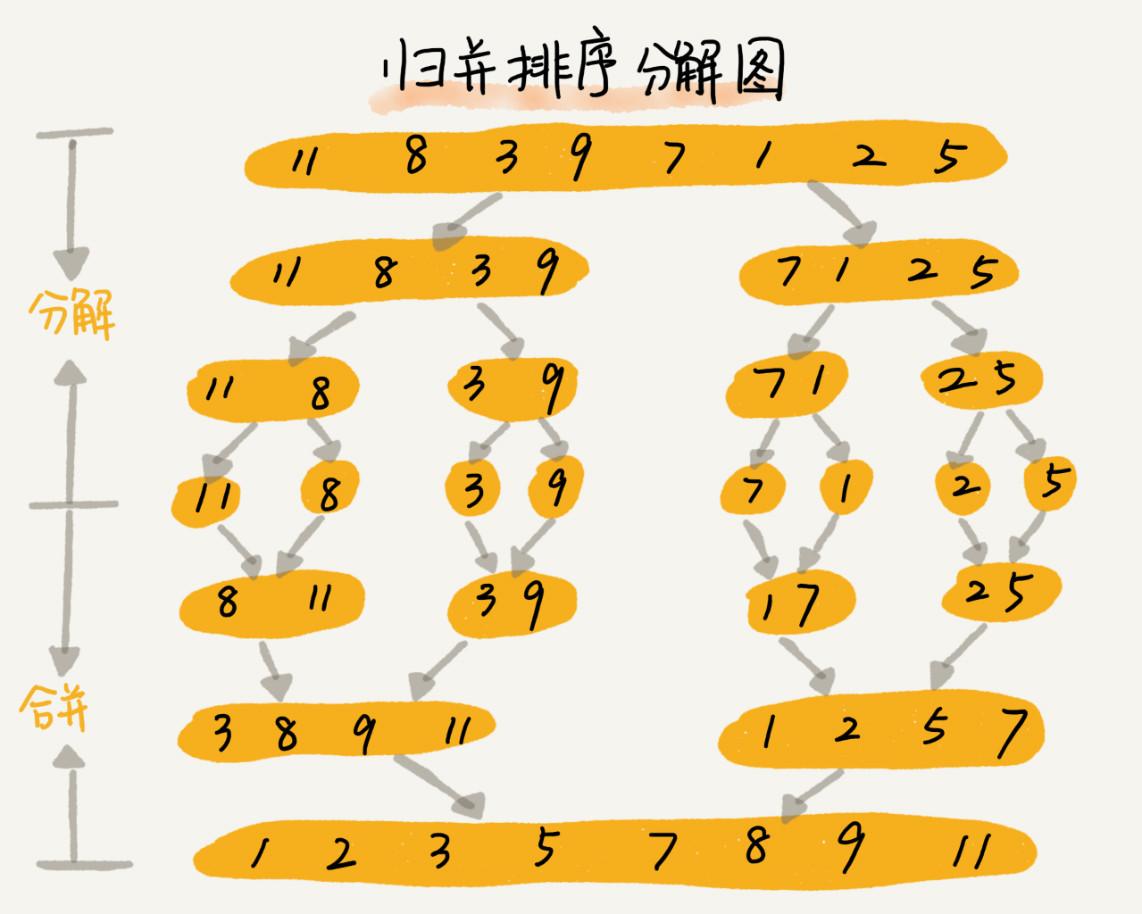
歸并排序是建立在歸并操作上的一種有效,穩定的排序算法。
該算法是采用分治思想,將已有序的子序列合并,得到完全有序的序列;
即先使每個子序列有序,再使子序列段間有序。若將兩個有序表合并成一個有序表,稱為二路歸并。
第一步:申請空間,使其大小為兩個已經排序序列之和,該空間用來存放合并后的序列
第二步:設定兩個指針,最初位置分別為兩個已經排序序列的起始位置
第三步:比較兩個指針所指向的元素,選擇相對小的元素放入到合并空間,并移動指針到下一位置
重復步驟3直到某一指針超出序列尾。
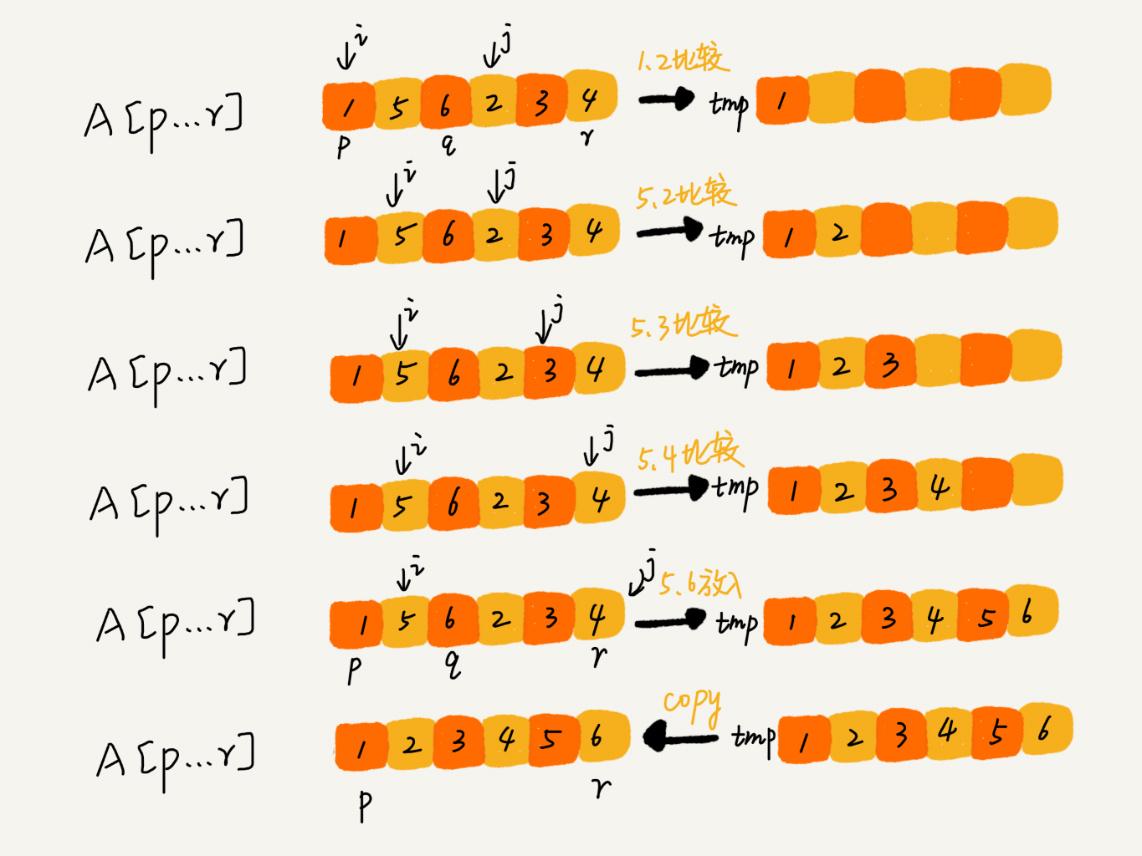
三、歸并排序代碼實現
import java.util.*;
class MergeSort {
public static void main(String[] args) {
int[] arr = {5,7,4,2,0,3,1,6};
mergeSort(arr, 0, arr.length-1);
System.out.print(Arrays.toString(arr));
}
public static void mergeSort(int[] arr,int left,int right){
if(left>=right){
return;
}
int mid = (left + right) / 2;
//先將數組按照中間下標分解成兩部分,遞歸直到分解每部分只有1個元素為止
mergeSort(arr, left, mid);
mergeSort(arr, mid+1, right);
//分解結束后,由下到上,遞歸合并已經排序好的兩部分
merge(arr, left, mid, right);
}
//需要注意的是整個合并過程中并沒有將兩個被合并的數組單獨拎出來,
//二者始終是存在于一個數組地址上的
public static void merge(int[] arr,int left,int mid,int right){
//根據拿到的左邊界,我們定其為第一個數組的指針
int s1 = left;
//根據中間位置,讓中間位置右移一個單位,那就是第二個數組的指針
int s2 = mid+1;
//根據左右邊界相減我們得到這片空間的長度,以此聲明額外空間
int[] temp = new int[right - left+1];
//定義額外空間的指針
int i = 0;
while(s1<=mid && s2 <=right){
//如果第一個數組的指針數值小于第二個數組的,那么其放置在臨時空間上
if(arr[s1]<=arr[s2]){
temp[i++] = arr[s1++];
}else{//否則是第二個數組的數值放置于其上
temp[i++] = arr[s2++];
}
}
//如果這是s1仍然沒有到達其終點,那么說明它還有剩
while(s1<=mid){
//因為我們知道每個參與合并的數組都是有序數組,因此直接往后拼接即可
temp[i++] = arr[s1++];
}
while(s2<=right){//同上
temp[i++] = arr[s2++];
}
for(int j = 0;j<temp.length;j++){//數組復制
arr[j+left] = temp[j];
}
}
}
二、歸并排序復雜度
時間復雜度O(N*logN)
空間復雜度O (N)
穩定性:穩定