什么是 DSA？

DSA（Data Structures and Algorithms）。

在計算機科學(xué)的背景下，術(shù)語 DSA 代表 數(shù)據(jù)結(jié)構(gòu)和算法。

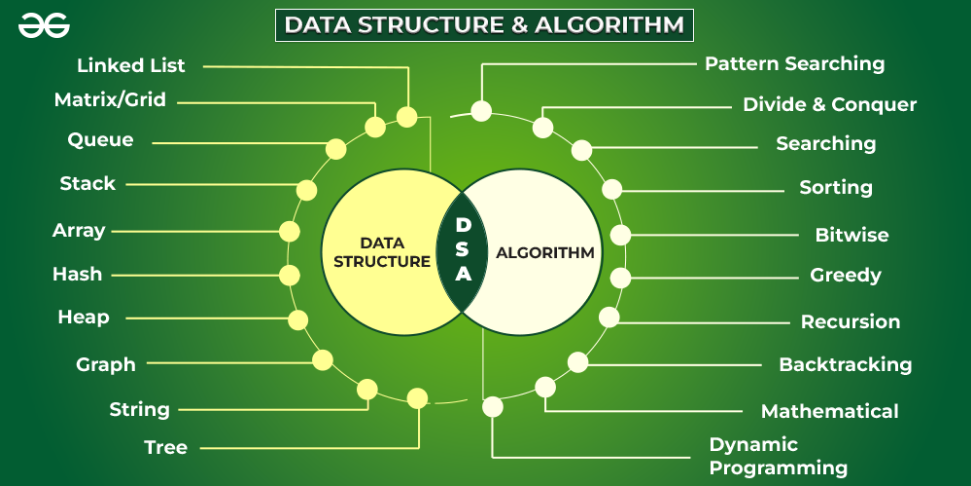
數(shù)據(jù)結(jié)構(gòu)與算法簡介（DSA）

什么是數(shù)據(jù)結(jié)構(gòu)？

數(shù)據(jù)結(jié)構(gòu)被定義為在我們的設(shè)備中存儲和組織數(shù)據(jù)以高效且有效地使用數(shù)據(jù)的特定方式。使用數(shù)據(jù)結(jié)構(gòu)背后的主要思想是最小化時間和空間復(fù)雜性。高效的數(shù)據(jù)結(jié)構(gòu)占用最少的內(nèi)存空間并需要最少的時間來執(zhí)行數(shù)據(jù)。

什么是算法？

算法被定義為一個過程或一組定義明確的指令，通常用于解決一組特定的問題或執(zhí)行特定類型的計算。簡單來說，就是為了執(zhí)行任務(wù)而按步驟的方式進行的一組操作。

認識DSA

時間和空間復(fù)雜性

這是一個有趣且重要的話題。使用 DSA 的主要動機是有效且高效地解決問題。如何判斷自己編寫的程序是否高效？這是通過復(fù)雜性來衡量的。復(fù)雜性有兩種類型：

• 時間復(fù)雜度：時間復(fù)雜度用于衡量執(zhí)行代碼所需的時間量。
• 空間復(fù)雜度：空間復(fù)雜度是指成功執(zhí)行代碼功能所需的空間量。

上述兩種復(fù)雜性都是根據(jù)輸入?yún)?shù)來測量的。但這里出現(xiàn)了一個問題。執(zhí)行代碼所需的時間取決于幾個因素，例如：

• 程序中執(zhí)行的操作數(shù)量。
• 以及設(shè)備的速度。
• 在平臺執(zhí)行時數(shù)據(jù)傳輸?shù)乃俣取?/span>

以下3種漸近符號主要用于表示算法的時間復(fù)雜度：

• Big-O 表示法 (Ο) – Big-O 表示法專門描述了最壞的情況。
• Omega 表示法 (Ω) – Omega(Ω) 表示法專門描述了最佳情況。
• Theta 表示法 (θ) – 該表示法表示算法的平均復(fù)雜度。

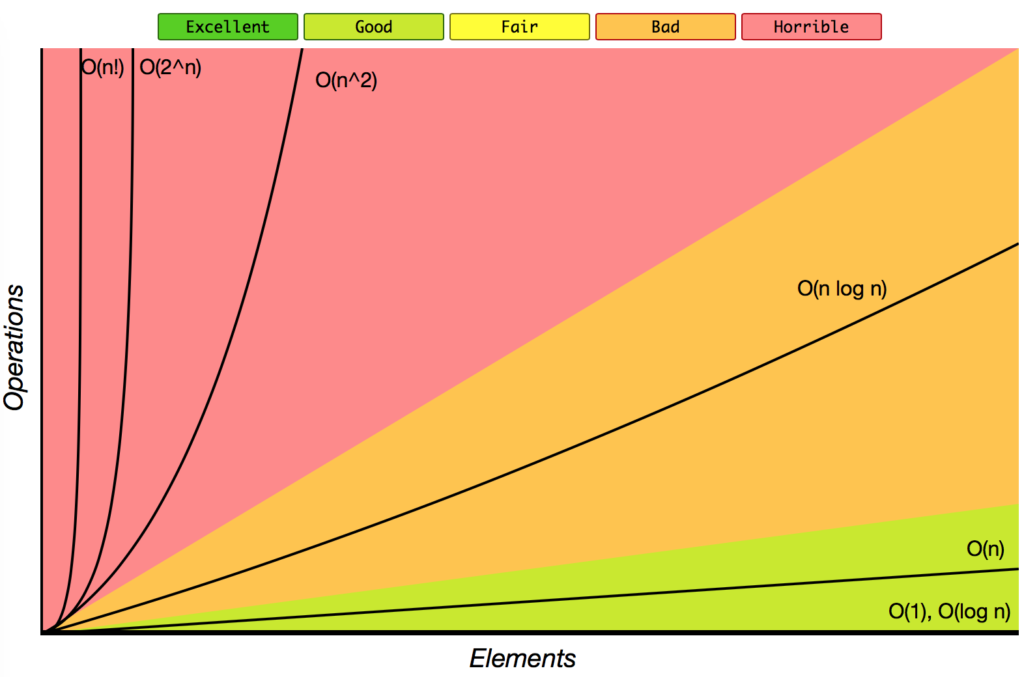
算法的增長率

PS：橫坐標：輸入數(shù)據(jù)的大小；縱坐標：執(zhí)行的完成時間。

代碼分析中最常用的表示法是Big O 表示法，它給出了代碼運行時間的上限（或輸入大小方面使用的內(nèi)存量）。

數(shù)據(jù)結(jié)構(gòu)

數(shù)組（Array）

最基本但重要的數(shù)據(jù)結(jié)構(gòu)是數(shù)組。它是一種線性數(shù)據(jù)結(jié)構(gòu)。數(shù)組是同類數(shù)據(jù)類型的集合，其中元素被分配連續(xù)的內(nèi)存。由于內(nèi)存的連續(xù)分配，數(shù)組的任何元素都可以在恒定時間內(nèi)訪問。每個數(shù)組元素都有一個對應(yīng)的索引號。

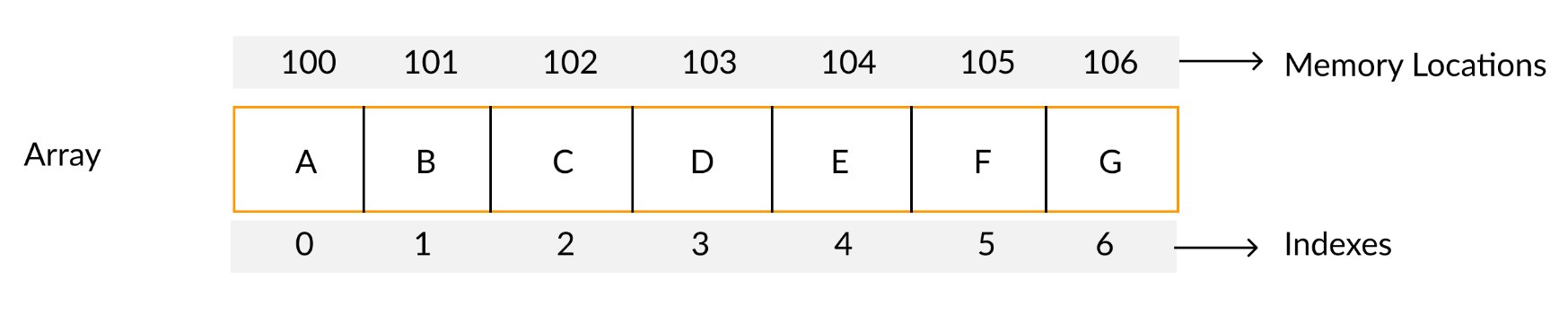
數(shù)組數(shù)據(jù)結(jié)構(gòu)

鏈表（Linked Lists）

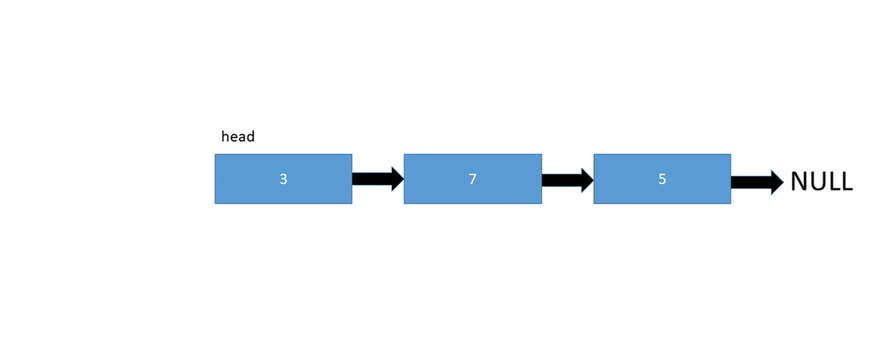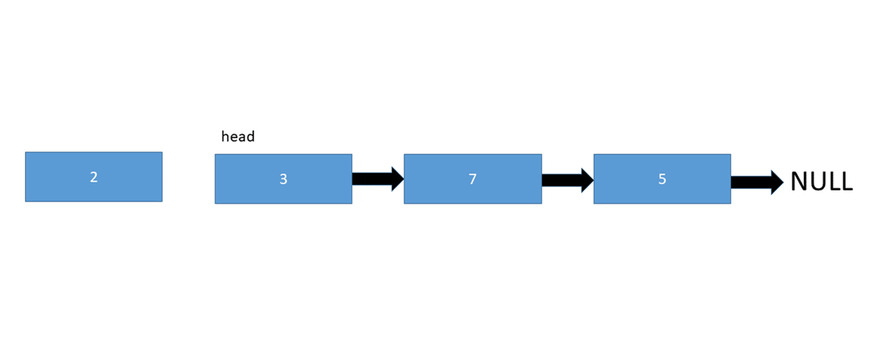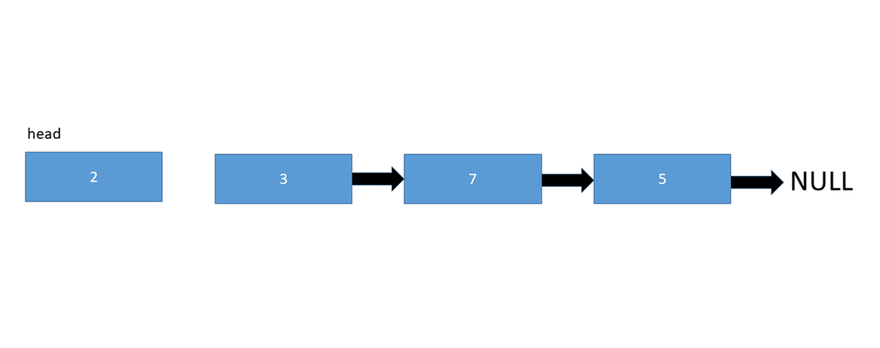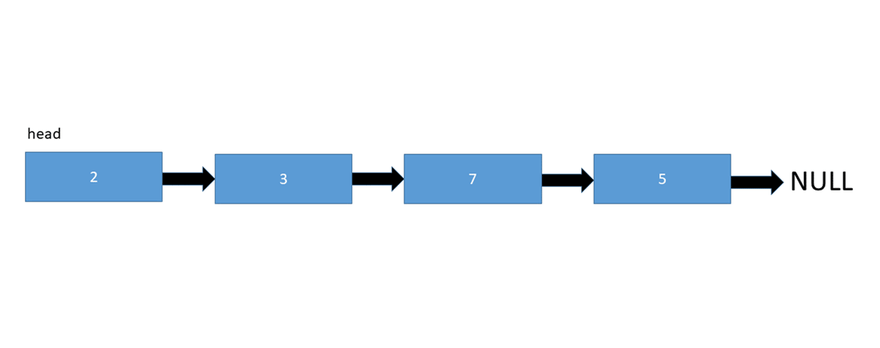
和上面的數(shù)據(jù)結(jié)構(gòu)一樣，鏈表也是一種線性數(shù)據(jù)結(jié)構(gòu)。但Linked List在配置上與Array不同。它沒有分配到連續(xù)的內(nèi)存位置。相反，鏈表的每個節(jié)點都被分配到一些隨機內(nèi)存空間，并且前一個節(jié)點維護一個指向該節(jié)點的指針。因此任何節(jié)點都不可能直接訪問內(nèi)存，而且它也是動態(tài)的，即鏈表的大小可以隨時調(diào)整。

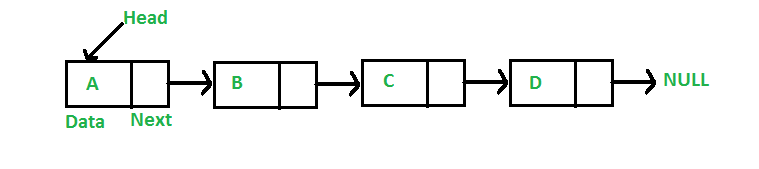
鏈表數(shù)據(jù)結(jié)構(gòu)

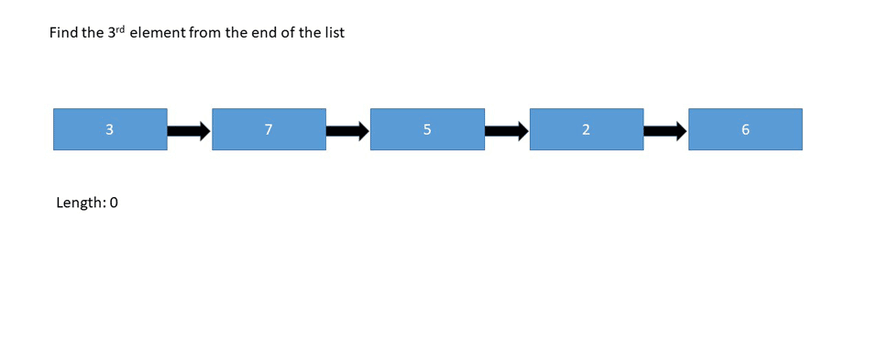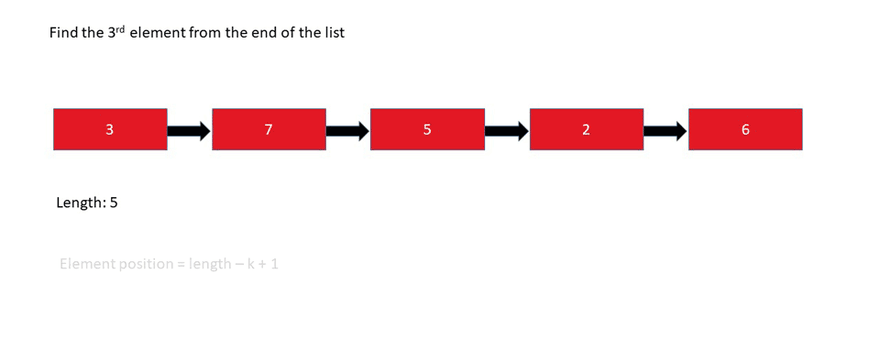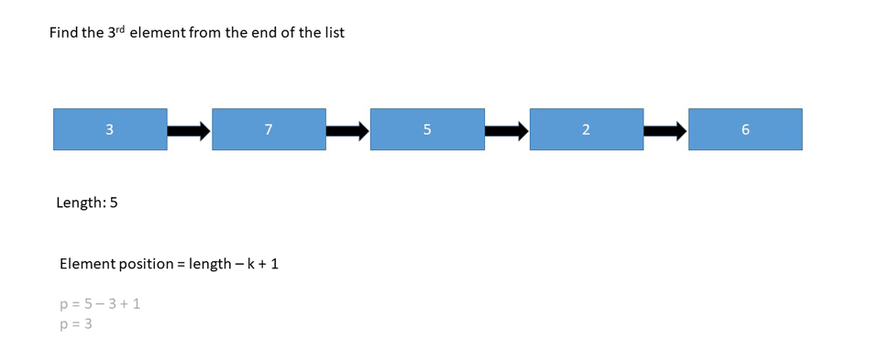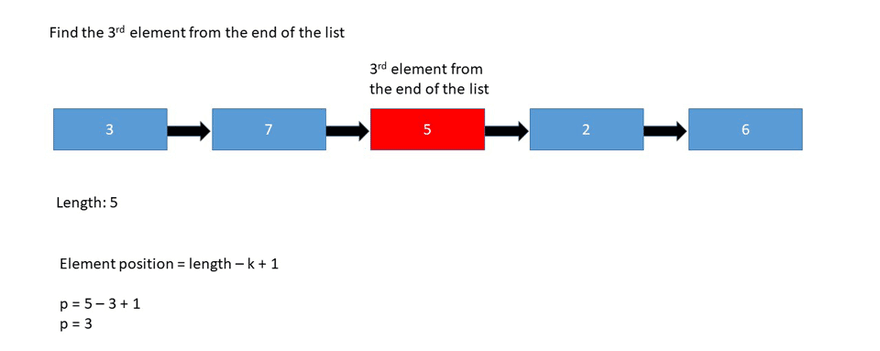
鏈表的不同實現(xiàn)：

• 單向鏈表– 鏈表中的每個節(jié)點僅指向其下一個節(jié)點。
• 循環(huán)鏈表——這是最后一個節(jié)點指向鏈表頭的鏈表類型。
• 雙向鏈表——在這種情況下，鏈表的每個節(jié)點都保存兩個指針，一個指向下一個節(jié)點，另一個指向前一個節(jié)點。

堆棧（Stack）

堆棧是一種線性數(shù)據(jù)結(jié)構(gòu)，遵循特定的操作執(zhí)行順序。順序可以是LIFO（后進先出）或 FILO（先進后出）。

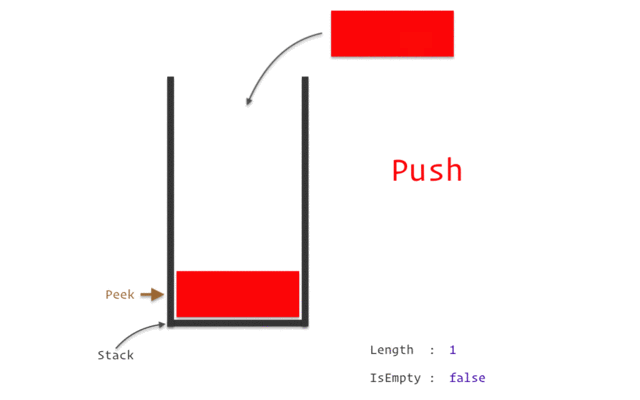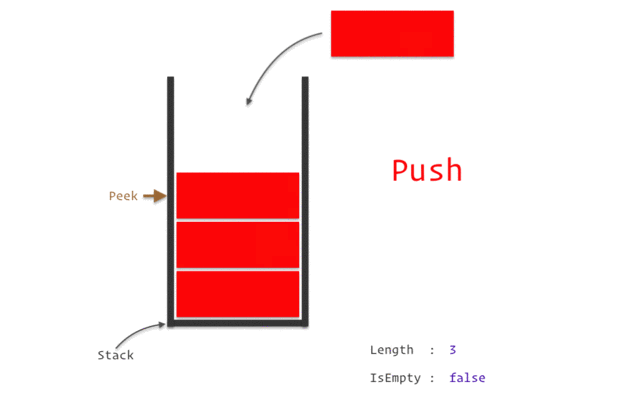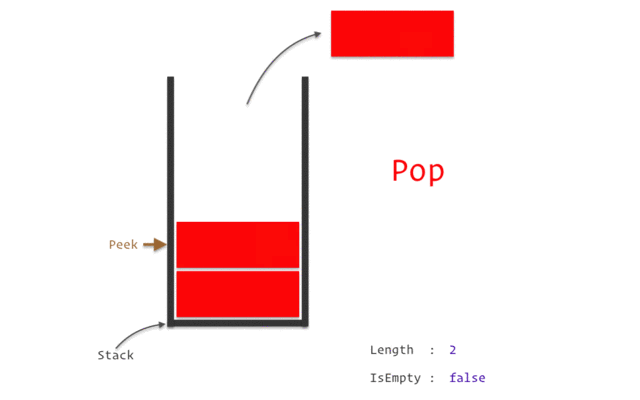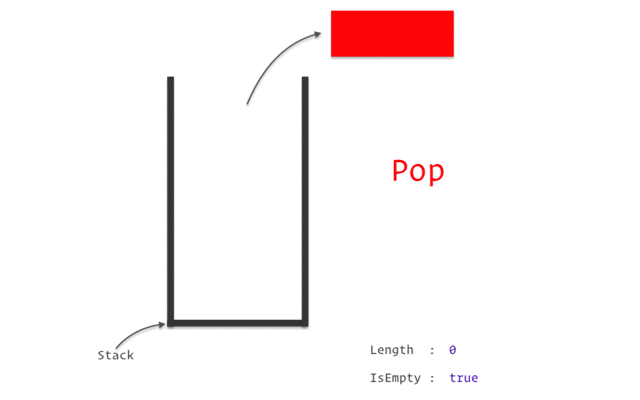
Stack之所以被認為是一種復(fù)雜的數(shù)據(jù)結(jié)構(gòu)，是因為它根據(jù)Stack數(shù)據(jù)結(jié)構(gòu)的特點和特點，使用了其他數(shù)據(jù)結(jié)構(gòu)來實現(xiàn)，比如數(shù)組、鏈表等。

隊列（Queue）

Stack類似但特性不同的數(shù)據(jù)結(jié)構(gòu)是Queue。

隊列是一種線性結(jié)構(gòu)，其各個操作遵循先進先出 (FIFO)方法。

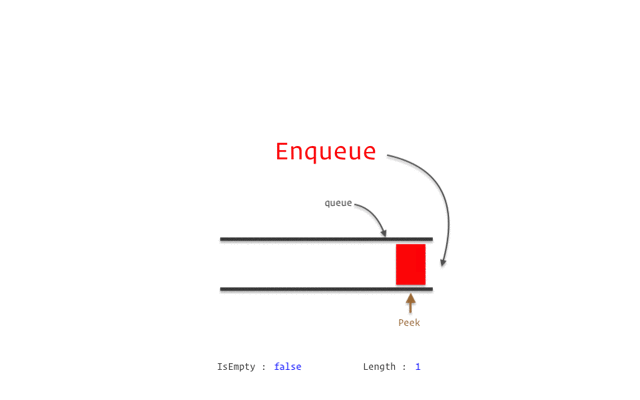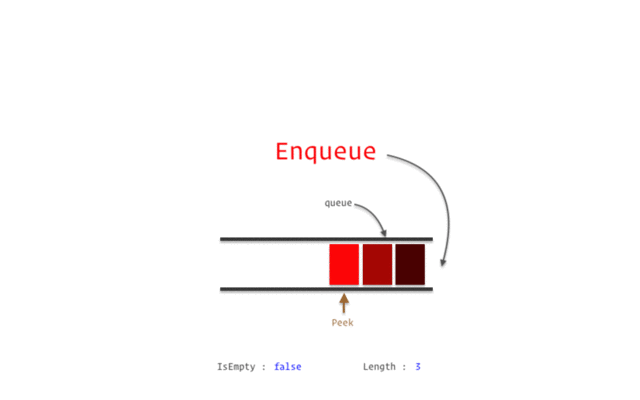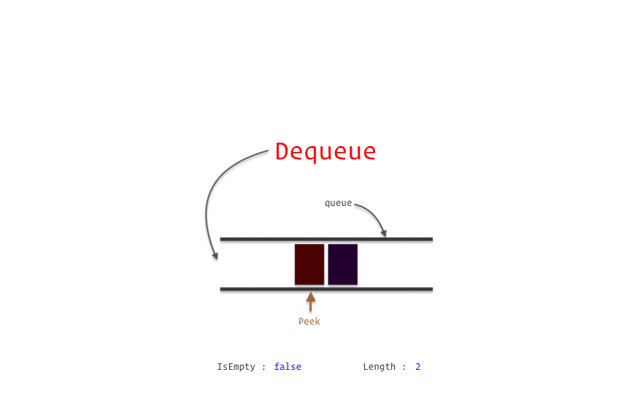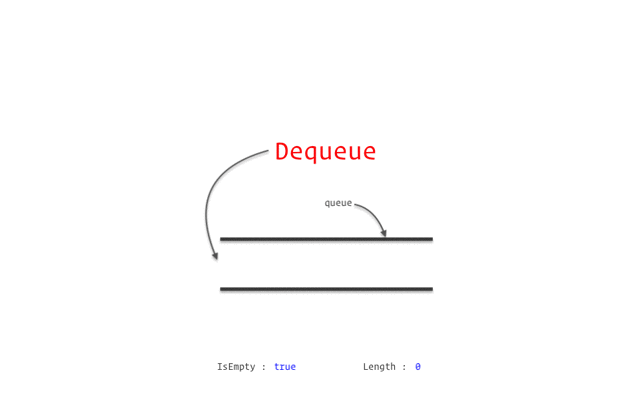
隊列可以有不同的類型，例如：

• 循環(huán)隊列——在循環(huán)隊列中，最后一個元素連接到隊列的第一個元素
• 雙端隊列（或稱為雙端隊列） ——雙端隊列是一種特殊類型的隊列，可以從隊列的兩端執(zhí)行操作。
• 優(yōu)先級隊列——這是一種特殊類型的隊列，其中元素按照其優(yōu)先級排列。低優(yōu)先級元素在高優(yōu)先級元素之后出列。

堆（Heap）

堆是一種特殊的基于樹的數(shù)據(jù)結(jié)構(gòu)，其中樹是完全二叉樹。

堆的類型：

一般來說，堆有兩種類型。

大頂堆：

在這個堆中，根節(jié)點的值必須是其所有子節(jié)點中最大的，并且其左右子樹也必須執(zhí)行相同的操作。

小頂堆：

在這個堆中，根節(jié)點的值必須是其所有子節(jié)點中最小的，并且其左右子樹也必須執(zhí)行相同的操作。

哈希（Hash）

散列是指使用稱為散列函數(shù)的數(shù)學(xué)公式從可變大小的輸入生成固定大小的輸出的過程。該技術(shù)確定數(shù)據(jù)結(jié)構(gòu)中項目存儲的索引或位置。

樹（Tree）

樹數(shù)據(jù)結(jié)構(gòu)類似于我們在自然界中看到的樹，但它是顛倒的。它也有根和葉。根是樹的第一個節(jié)點，葉子是最底層的節(jié)點。樹的特點是從它的任何一個節(jié)點到任何其他節(jié)點只有一條路徑。

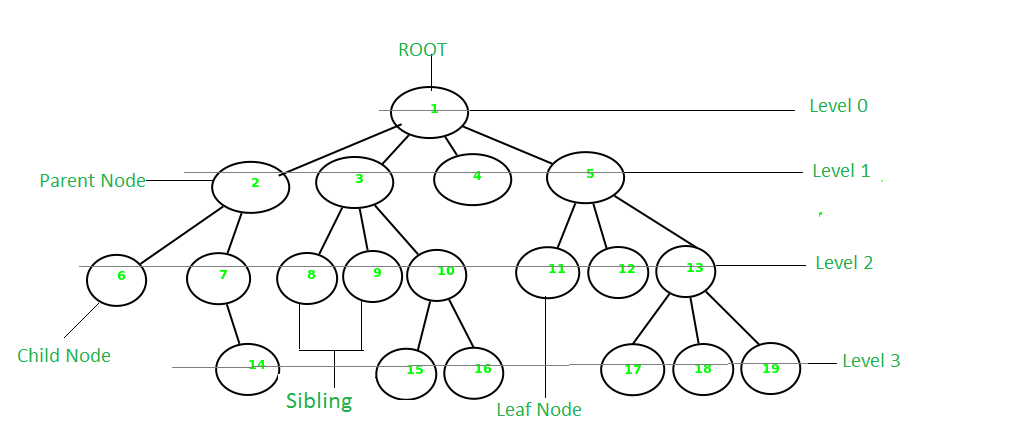
樹數(shù)據(jù)結(jié)構(gòu)

樹有多種不同的類型和變種，常見的樹包括：

• 二叉樹（Binary Tree）：每個節(jié)點最多有兩個子節(jié)點，分別稱為左子節(jié)點和右子節(jié)點。
• 二叉搜索樹（Binary Search Tree）：二叉樹的一種特殊形式，其中左子節(jié)點的值小于等于父節(jié)點的值，右子節(jié)點的值大于等于父節(jié)點的值，便于進行快速的搜索和插入操作。
• 平衡樹（Balanced Tree）：樹的節(jié)點在高度上保持平衡，以確保樹的操作具有良好的性能。常見的平衡樹包括AVL樹、紅黑樹等。
• 堆（Heap）：一種特殊的樹結(jié)構(gòu)，用于高效地找到最大值或最小值。常見的堆包括最大堆和最小堆。
• B樹（B-tree）：一種多路搜索樹，常用于數(shù)據(jù)庫和文件系統(tǒng)等存儲系統(tǒng)，具有高度的平衡性和高效的查找操作。

圖（Graph）

它類似于Tree數(shù)據(jù)結(jié)構(gòu)，不同之處在于沒有特定的根或葉節(jié)點，并且可以按任意順序遍歷。

圖是一種非線性數(shù)據(jù)結(jié)構(gòu)，由一組有限的頂點（或節(jié)點）和一組連接一對節(jié)點的邊組成 。

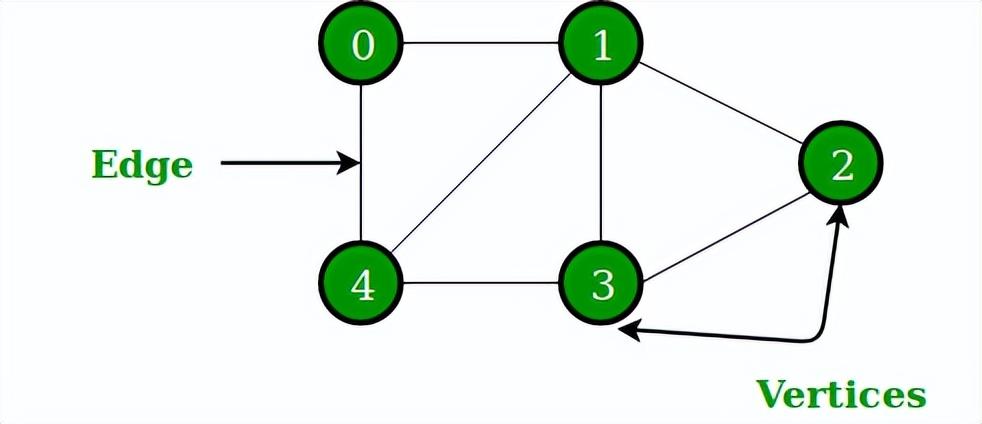
圖數(shù)據(jù)結(jié)構(gòu)

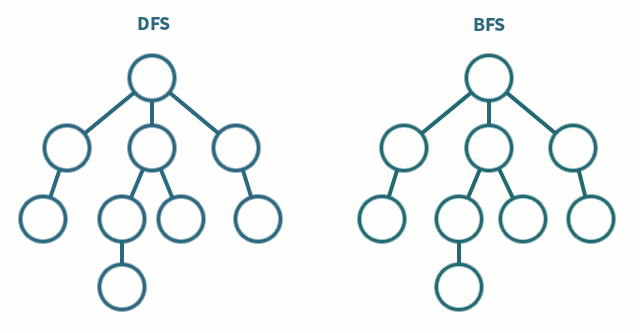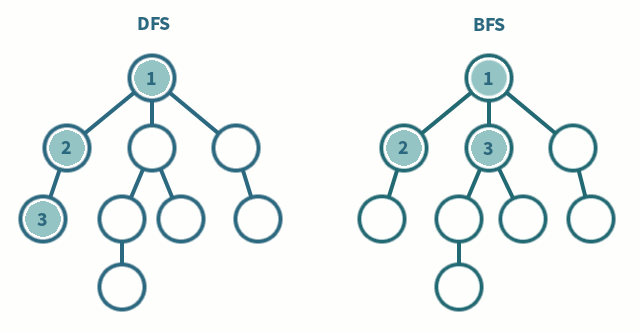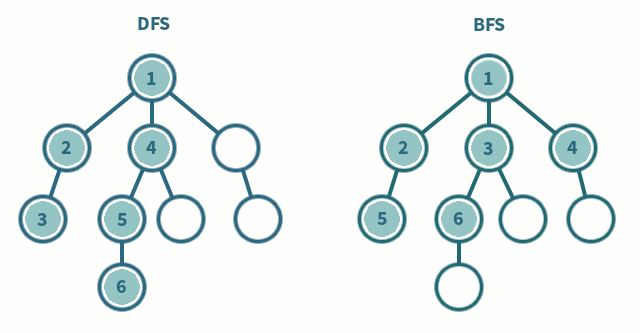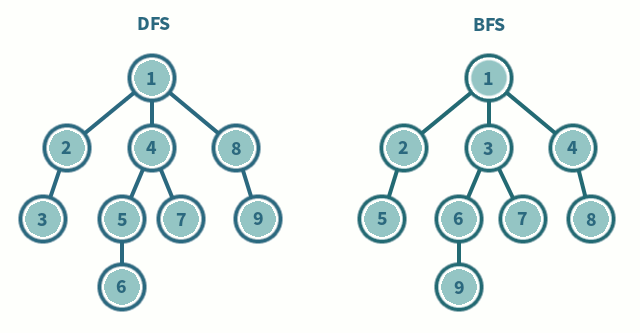
每條邊都顯示一對節(jié)點之間的連接。這種數(shù)據(jù)結(jié)構(gòu)有助于解決許多現(xiàn)實生活中的問題。根據(jù)邊和節(jié)點的方向，有各種類型的圖。

以下是一些必須了解的圖概念：

• 圖的類型：根據(jù)節(jié)點的連通性或權(quán)重，有不同類型的圖。
• BFS 和 DFS ： 這些是遍歷圖的算法
• 圖中的循環(huán)：循環(huán)是一系列連接，我們將在循環(huán)中移動這些連接。
• 圖中的拓撲排序
• 圖中的最小生成樹

算法

搜索算法

搜索算法用于查找數(shù)組、字符串、鏈表或其他數(shù)據(jù)結(jié)構(gòu)中的特定元素。

最常見的搜索算法是：

• 線性搜索- 在此搜索算法中，我們從一端到另一端迭代地檢查元素。
• 二分搜索——在這種類型的搜索算法中，我們將數(shù)據(jù)結(jié)構(gòu)分成兩個相等的部分，并嘗試決定需要在哪一半中查找元素。
• 三元搜索——在這種情況下，數(shù)組被分為三個部分，根據(jù)分區(qū)位置的值，我們決定需要在哪個段中查找所需元素。

除此之外，還有其他搜索算法，例如

• 跳轉(zhuǎn)搜索
• 插值搜索
• 指數(shù)搜索

排序算法

通常我們需要根據(jù)特定條件對數(shù)據(jù)進行排列或排序。排序算法就是在這些情況下使用的算法。根據(jù)條件，我們可以對一組同質(zhì)數(shù)據(jù)進行排序，就像按升序或降序?qū)?shù)組進行排序一樣。

排序算法用于根據(jù)元素上的比較運算符重新排列給定的數(shù)組或列表元素。比較運算符用于決定相應(yīng)數(shù)據(jù)結(jié)構(gòu)中元素的新順序。

顯示排序的示例

有許多不同類型的排序算法。一些廣泛使用的算法是：

• 快速排序
• 歸并排序
• 堆排序
• 冒泡排序
• 插入排序
• 選擇排序
• 樹排序
• 等等

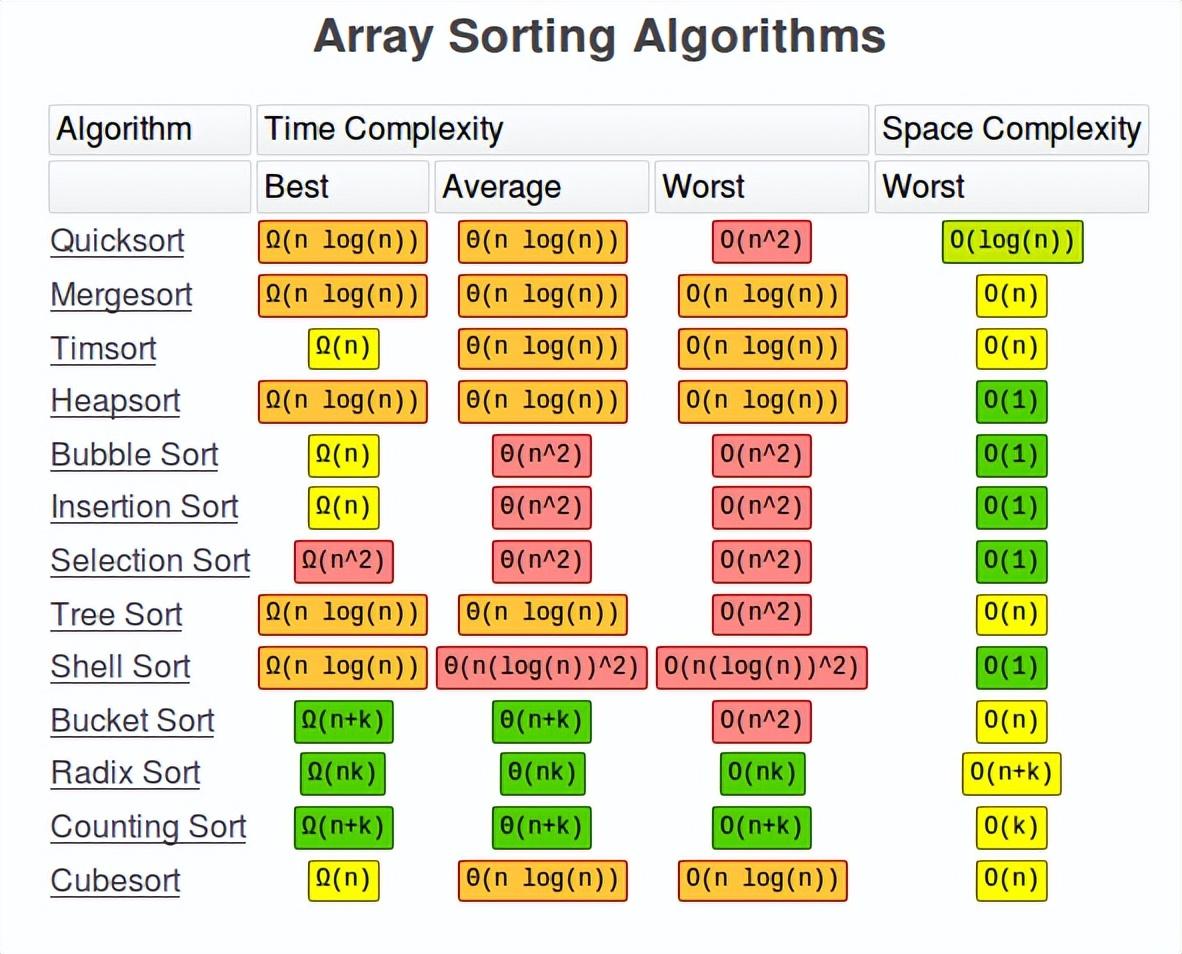
排序算法的復(fù)雜性

分治算法

顧名思義，它將問題分解為多個部分，然后解決每個部分，然后再次合并已解決的子任務(wù)以解決實際問題。

分而治之是一種算法范式。典型的分而治之算法使用以下三個步驟解決問題。

• 分解（Divide）：將給定問題分解為相同類型的子問題。
• 解決（Conquer）：遞歸地解決這些子問題。
• 合并（Combine）：將子問題合并為原始問題的解決方案。

這是前面提到的歸并排序和快速排序這兩種排序算法中提到的主要技術(shù)。

貪心算法

顧名思義，該算法一次構(gòu)建一個解決方案，并選擇下一個提供最明顯和直接好處的解決方案，即當(dāng)時的最佳選擇。因此，選擇局部最優(yōu)也導(dǎo)致全局解決方案的問題最適合貪婪。

例如，考慮分數(shù)背包問題。局部最優(yōu)策略是選擇具有最大價值與重量比的項目。這種策略還可以產(chǎn)生全局最優(yōu)解決方案，因為我們可以獲取某個項目的一部分。

回溯算法

回溯算法源自遞歸算法，如果遞歸解決方案失敗，則可以選擇恢復(fù)，即如果解決方案失敗，程序?qū)⒆匪莸绞〉臅r刻并構(gòu)建另一個解決方案。所以基本上它會嘗試所有可能的解決方案并找到正確的解決方案。

回溯是一種遞歸解決問題的算法技術(shù)，通過嘗試逐步構(gòu)建解決方案，一次一個部分，刪除那些在任何時間點都無法滿足問題約束的解決方案

動態(tài)規(guī)劃

動態(tài)編程主要是對普通遞歸的優(yōu)化。無論何時我們看到重復(fù)調(diào)用相同輸入的遞歸解決方案，我們都可以使用動態(tài)編程對其進行優(yōu)化。

動態(tài)規(guī)劃算法的主要思想是利用先前計算的結(jié)果來避免同一子任務(wù)的重復(fù)計算，從而有助于降低時間復(fù)雜度。

動態(tài)規(guī)劃

圖算法

圖算法用于解決將圖表示為網(wǎng)絡(luò)的問題，例如航空公司航班、互聯(lián)網(wǎng)如何連接或 社交軟件里人之間親密度。它們在NLP和機器學(xué)習(xí)中也很流行，用于形成網(wǎng)絡(luò)。

一些頂級的圖形算法包括：

• 實現(xiàn)廣度優(yōu)先遍歷
• 實現(xiàn)深度優(yōu)先遍歷
• 計算圖級別中的節(jié)點數(shù)
• 查找兩個節(jié)點之間的所有路徑
• 查找圖的所有連通分量
• 迪杰斯特拉算法（Dijkstra） 在圖數(shù)據(jù)中查找最短路徑
• 移除邊緣

總結(jié)

本篇是從理論和概念上對數(shù)據(jù)結(jié)構(gòu)與算法的一些簡單介紹，后面會詳細解釋數(shù)據(jù)結(jié)構(gòu)和算法。