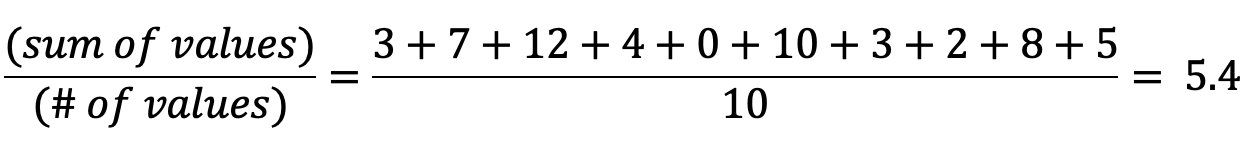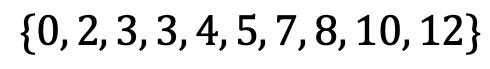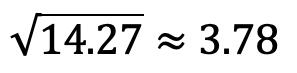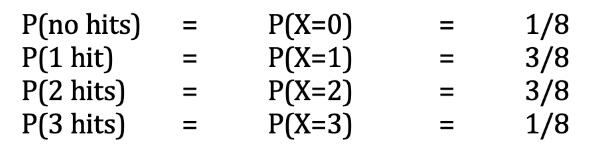每個數據科學家都必須了解的5大統計概念
統計和數據科學的重要支柱
任何數據科學家都可以從數據集中收集信息-任何優秀的數據科學家都將知道,扎實的統計基礎可以收集有用和可靠的信息。 沒有它,就不可能進行高質量的數據科學。
> Photo by Tachina Lee on Unsplash
但是統計是一個巨大的領域! 我從哪說起呢?
以下是每個數據科學家都應該知道的前五個統計概念:描述性統計,概率分布,降維,過采樣和欠采樣以及貝葉斯統計。
讓我們從最簡單的一個開始。
1. 描述性統計
您正坐在數據集的前面。 您如何對自己所擁有的東西有一個高層次的描述? 描述性統計就是答案。 您可能已經聽說過其中的一些:平均值,中位數,眾數,方差,標準差…
這些將快速識別您的數據集的關鍵特征,并在您執行任務時通知您的方法。 讓我們來看看一些最常見的描述性統計數據。
意思
平均值(也稱為"期望值"或"平均值")是值的總和除以值的數量。 采取以下示例集:
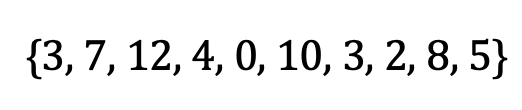
平均值計算如下:
中位數
以升序(或降序)列出您的值。 中位數是將數據分成兩半的點。 如果有兩個中間數字,則中位數是這些數字的平均值。 在我們的示例中:
中位數為4.5。
模式
模式是數據集中最頻繁的值。 在我們的示例中,模式為3。
方差
方差衡量數據集相對于均值的分布。 要計算方差,請從每個值中減去平均值。 平方每個差異。 最后,計算這些結果數字的平均值。 在我們的示例中:
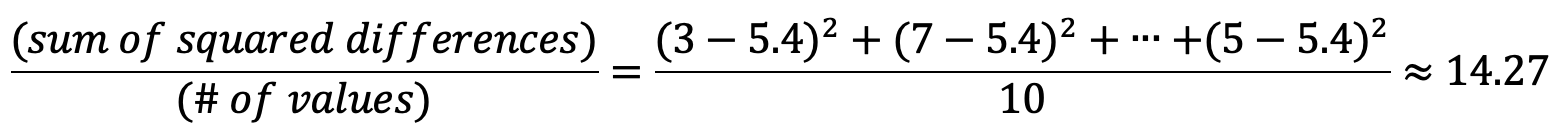
標準偏差
標準差用于衡量總體價差,并通過求出方差的平方根來計算。 在我們的示例中:
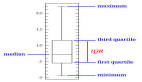
其他描述性統計數據包括偏度,峰度和四分位數。
2. 概率分布
概率分布是一種函數,它給出實驗每個可能結果的出現概率。 如果您要繪制鐘形曲線,那您就走對了。 乍一看,它顯示了如何分散隨機變量的值。 隨機變量及其分布可以是離散的也可以是連續的。
離散的
約翰是一名棒球運動員,每次向他投球時,都有50%的隨機擊球機會。 讓我們向約翰投三個球,看看他有多少次擊球。 以下是所有可能結果的列表:

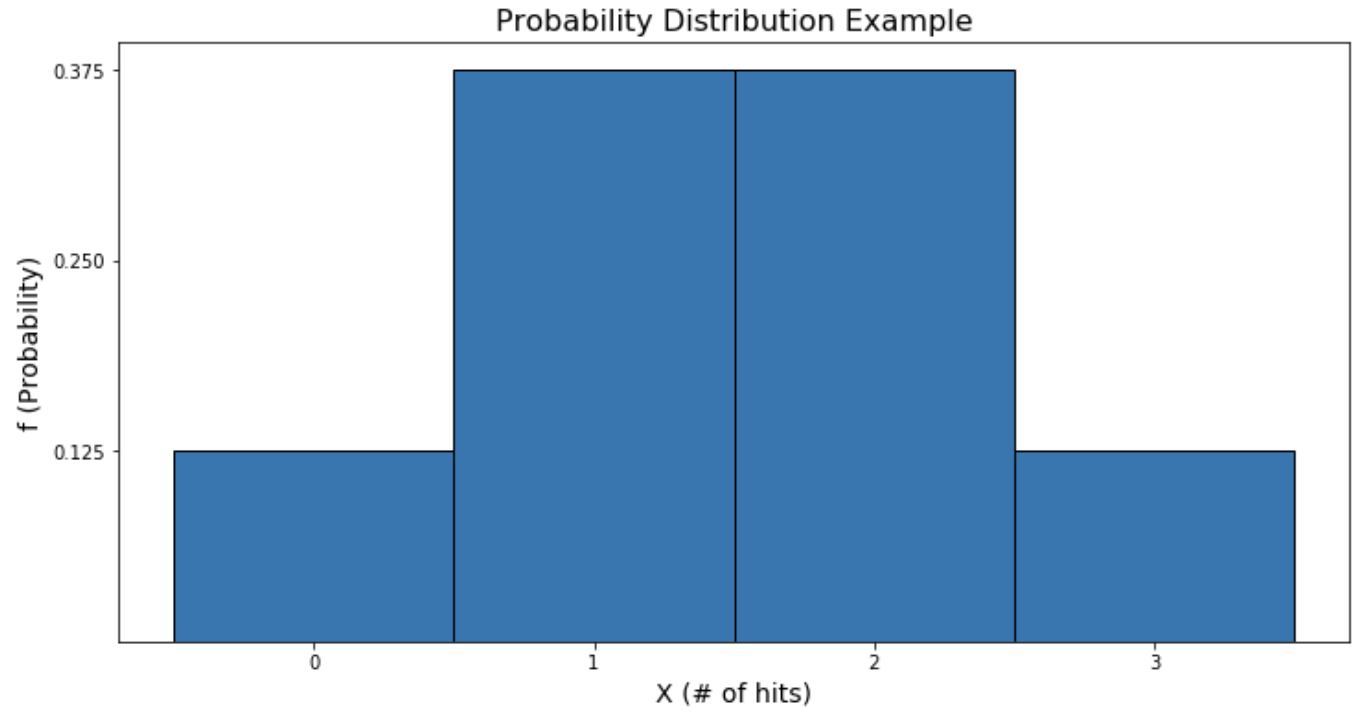
令X為我們的隨機變量,即約翰在三音高實驗中被擊中的次數。 約翰獲得n次點擊的概率由P(X = n)表示。 因此,X可以為0、1、2或3。如果上述所有八個結果均具有相同的可能性,則我們有:
用f代替P,我們就有了概率函數! 讓我們來畫一下。
從圖中可以看出,John獲得1或2次命中比獲得0或3次命中的可能性更大,因為對于那些X值,該圖更高。常見的離散分布包括伯努利,二項式和 泊松
連續
連續情況自然而然地來自離散情況。 除了計算命中率外,我們的隨機變量可能是棒球播出的時間。 我們可以將值設置為3.45秒或6.98457秒,而不僅僅是一秒,兩秒或三秒。
我們正在談論無限多種可能性。 連續變量的其他示例是高度,時間和溫度。 常見的連續分布包括正態,指數和卡方。
3. 降維
如果輸入變量太多或數據計算笨拙,則可以轉向降維。 這是將高維數據投影到低維空間的過程,但是請務必注意不要丟失原始數據集的重要特征。
例如,假設您正在嘗試確定哪些因素可以最好地預測您最喜歡的籃球隊今晚能否贏得比賽。 您可能會收集數據,例如他們的獲勝百分比,他們在踢球,在哪里踢球,他們的前鋒是誰,他吃晚餐的時間以及教練穿什么顏色的鞋子。
您可能會懷疑其中某些功能比其他功能與獲勝的相關性更高。 降維可以使我們放心地刪除不會對預測做出有意義貢獻的信息,同時保留具有最大預測價值的特征。
主成分分析(PCA)是一種流行的方法,它通過夸大稱為主成分的要素的新組合的方差來工作。 這些新組合是原始數據點到新空間(仍是相同維度)的投影,其中會顯示變化。
通常的想法是,在這些新組件中,變化最小的組件可以最安全地刪除。 刪除單個組件將使原始尺寸減小一倍,刪除兩個組件將使尺寸減小兩個,依此類推。
4. 欠采樣和過采樣
收集的一組觀測值稱為"樣本",而收集觀測值的方式稱為"采樣"。 在需要平等代表少數派和多數派的分類情況下,欠采樣或過采樣可能會有用。 對多數類別進行欠采樣或對少數類別進行過度采樣可以幫助均衡不平衡的數據集。
隨機過采樣(或者,隨機欠采樣)涉及在少數類中隨機選擇和復制觀測值(或在多數類中隨機選擇和刪除觀測值)。
這很容易實現,但是您應謹慎行事:對采樣重復的觀測值進行過采樣加權,如果不加偏見,可能會嚴重影響結果。 同樣,采樣不足會帶來刪除關鍵觀測值的風險。
少數群體過采樣的一種方法是合成少數群體過采樣技術(SMOTE)。 這通過創建現有觀測值的新組合來創建(綜合)少數群體觀測值。 對于少數群體類別中的每個觀察,SMOTE會計算其k個最近的鄰居; 也就是說,它找到最類似于該觀測值的k個少數群體觀測值。
通過將觀察結果視為向量,它可以通過用0到1之間的隨機數對k個最近鄰居中的任何一個加權,并將其添加到原始向量中來創建隨機線性組合。
多數類樣本不足的一種方法是使用聚類質心。 從理論上講,與SMOTE相似,它用k個最近鄰居簇的質心替換向量組。
5. 貝葉斯統計
在統計推斷方面,主要有兩種思想流派:常客統計和貝葉斯統計。 頻繁的統計數據使我們能夠進行有意義的工作,但是在某些情況下,它的工作還不夠。 當您有理由相信您的數據可能無法很好地表示您希望將來觀察到的數據時,貝葉斯統計量會很好。
這使您可以將自己的知識整合到計算中,而不僅僅是依靠樣本。 它還可以讓您在收到新數據后更新對未來的看法。
來看一個例子:A隊和B隊互相比賽10次,A隊贏得9次。 如果今晚兩隊互相比賽,我問你認為誰會贏,你可能會說A隊! 如果我還告訴您B隊賄賂了今晚的裁判怎么辦? 好吧,那您可能會猜猜B隊會贏。
貝葉斯統計允許您將這些額外的信息納入您的計算中,而常客統計則僅關注10個獲勝百分比中的9個。
貝葉斯定理是關鍵:
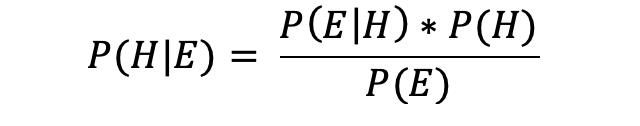
給定E的H的條件概率,記為P(H | E),表示當E也出現(或已經發生)時H發生的概率。 在我們的示例中,H是B隊獲勝的假設,E是我為您提供的有關B隊賄賂裁判的證據。
P(H)是常客概率,為10%。 P(E | H)是在B隊獲勝的情況下我對您所說的關于賄賂的信息屬實的概率。 (如果B隊今晚獲勝,您會相信我說的話嗎?)
最后,P(E)是B隊實際上賄賂裁判的概率。 我是值得信賴的信息來源嗎? 您會發現,這種方法不僅包含了兩支球隊之前10場比賽的結果,而且還包含更多信息。
就是今天。 讓我們在下一節中總結一下。
你走之前
學習這5個概念并不能使您掌握統計學或數據科學知識,但是如果您不了解數據科學項目的基本流程,那么這是一個很好的起點。