用Python 通過動態規劃完成公務員考試題
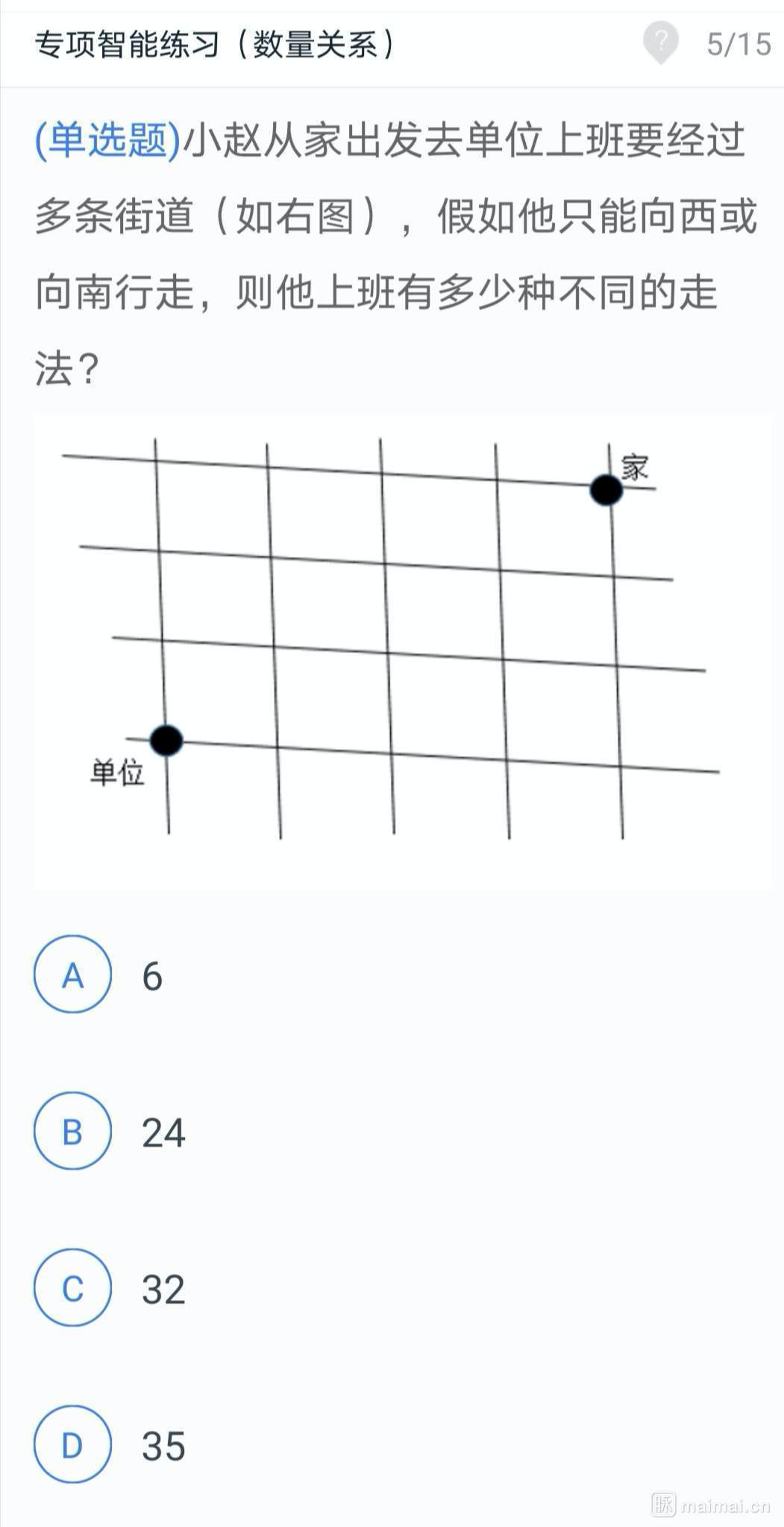
今天在脈脈上看到有人發了一道公務員的考試題,題目如下:
這道題可以用數學方法來做,但我離開學校很多年了,想不出數學的解法。不過看到題目的一瞬間,我就想到了可以使用動態規劃來解決這個問題。
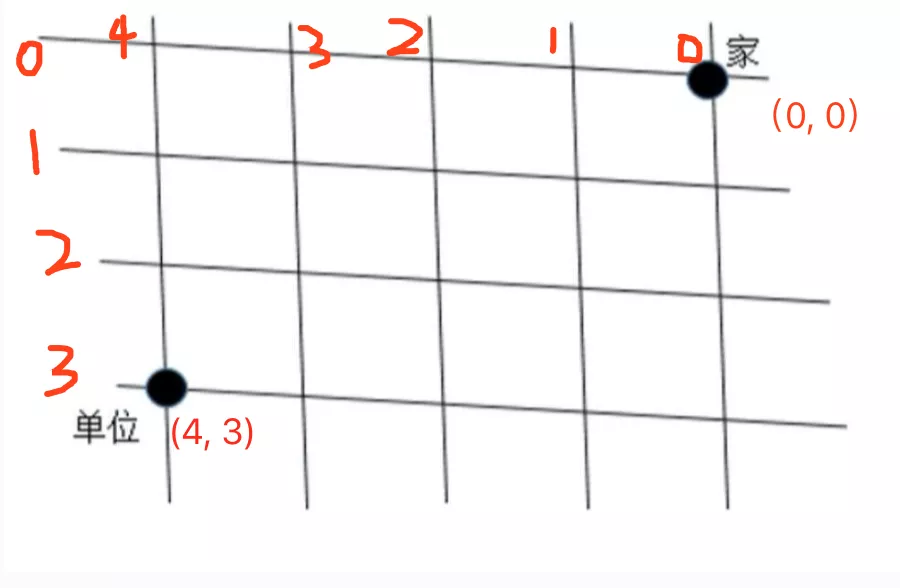
我們把“家”的位置標記為(0, 0),把單位的位置標記為(4, 3),如下圖所示:
動態規劃的一個典型解法,就是想問題的時候,倒著想。假設現在我已經在單位(4, 3)了。我上一步是在哪里?要到(4, 3),只有兩種方法,從(3, 3)到(4, 3)或者從(4, 2)到(4, 3)。現在問題的規模縮小了,變成了兩個小問題,一個是從家(0, 0)到(4, 2)有多少種走法,另一個是從家(0, 0)到(3, 3)有多少種走法。
到這里,我們看出來這實際上是一個遞歸問題,也就是fn(x, y) = f(x - 1, y) + f(x, y - 1)。
不過,這里要考慮另一個問題,就是當我們在fn(x, 0)或者fn(0, y)的時候。如果 x > 1,那么此時只有一種走法,就是從(x-1, 0)到 (x, 0)。如果x == 1,那么此時只能是從(0, 0)到(1, 0)。同理,對于(0, y)也是一樣,如果y > 1,那么只能從(0, y - 1)到(0, y)。如果y == 1,那么只能是從(0, 0)到(0, 1)。
于是,根據這個思路,我們可以寫出如下的代碼:
- def find_walk_num(x, y):
- if y == 0:
- if x == 1:
- return 1
- return find_walk_num(x - 1, 0)
- if x == 0:
- if y == 1:
- return 1
- return find_walk_num(0, y - 1)
- return find_walk_num(x - 1, y) + find_walk_num(x, y - 1)
- result = find_walk_num(4, 3)
- print(f'從(0, 0)到(4, 3)的走法一共有:{result}種')
運行效果如下圖所示:
所以這道題的答案就是 D,一共有35種走法。