快速排序算法實現及優化
本文轉載自微信公眾號「貝塔學JAVA」,作者Silently9527。轉載本文請聯系貝塔學JAVA公眾號。
本文已被Github倉庫收錄 https://github.com/silently9527/JavaCore
程序員常用的IDEA插件:https://github.com/silently9527/ToolsetIdeaPlugin
完全開源的淘客項目:https://github.com/silently9527/mall-coupons-server
前言
快速排序可以說是使用最廣的排序算法了,主要的特點是基于原地排序(不需要使用輔助數組,節省空間);其實對于長度為N的數組使用快速排序時間復雜度為 NlogN;在前幾篇也一起討論了其他的排序算法,都沒能夠把這兩個特點結合起來。
快速排序思路
快速排序也是一種分治的排序算法,把數組劃分為兩個子數組,然后遞歸對子數組進行排序,最終保證整個數組有序。
算法思路:
- 隨機選擇一個切分元素,通常選擇的是數組的第一個元素
- 從數組的左邊開始掃描找出大于等于切分元素的值,從數組的右邊開始掃描找出小于等于切分元素的值,交換這兩個值
- 循環這個過程直到左右兩個指針相遇,這樣就排定了一個元素,保證了切分元素左邊的值都是小于它的值,右邊的元素都是大于它的值
- 遞歸這個過程,最終保證整個數組有序
算法實現
根據快速排序算法的思路,我們可以寫出第一版實現:
- public class QuickSort implements SortTemplate {
- @Override
- public void sort(Comparable[] array) {
- quickSort(array, 0, array.length - 1);
- }
- private void quickSort(Comparable[] array, int lo, int hi) {
- if (lo >= hi) {
- return;
- }
- int partition = partition(array, lo, hi);
- quickSort(array, lo, partition - 1);
- quickSort(array, partition + 1, hi);
- }
- private int partition(Comparable[] array, int lo, int hi) {
- int i = lo, j = hi + 1;
- Comparable el = array[lo];
- while (true) {
- while (less(array[++i], el)) {
- if (i == hi) {
- break;
- }
- }
- while (less(el, array[--j])) {
- if (j == lo) {
- break;
- }
- }
- if (i >= j) {
- break;
- }
- exch(array, i, j);
- }
- exch(array, lo, j);
- return j;
- }
- }
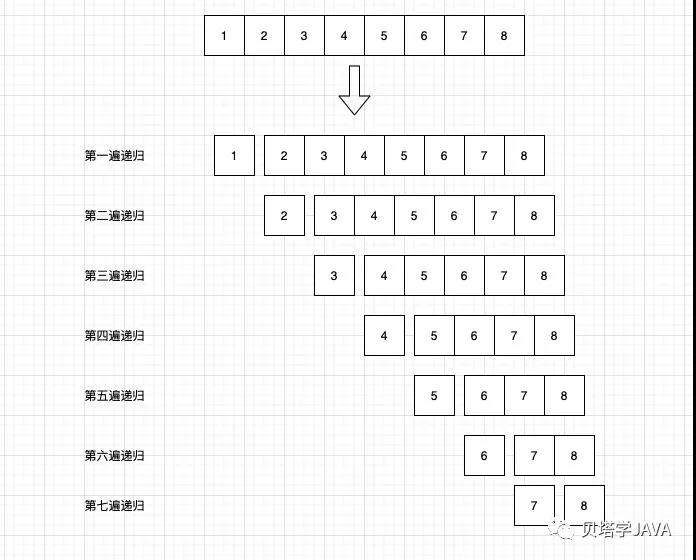
這段代碼是實現快速排序的常規實現,考慮最糟糕的情況,假如需要排序的數組是已經有序的[1,2,3,4,5,6,7,8],執行快速排序的過程如圖:
對一個長度為N的數組,最糟糕的情況下需要遞歸N-1次,所以時間復雜度是O(n2),為了避免這種情況出現,我們來看下算法如何改進
算法改進
- 保證隨機性 為了避免最糟糕的情況出現,有兩個辦法,第一是在排序數組之前先隨機打亂數組;第二是在partition方法中隨機取切分元素,而不是固定取第一個,簡單實現:
- private int partition(Comparable[] array, int lo, int hi) {
- int i = lo, j = hi + 1;
- int random = new Random().nextInt(hi - lo) + lo;
- exch(array, lo, random);
- Comparable el = array[lo];
- while (true) {
- while (less(array[++i], el)) {
- if (i == hi) {
- break;
- }
- }
- while (less(el, array[--j])) {
- if (j == lo) {
- break;
- }
- }
- if (i >= j) {
- break;
- }
- exch(array, i, j);
- }
- exch(array, lo, j);
- return j;
- }
- 切換到插入排序 這點和歸并排序一樣,對于小數組的排序直接切換成插入排序
- private void quickSort(Comparable[] array, int lo, int hi) {
- if (lo >= hi) {
- return;
- }
- if (hi - lo < 5) { //測試,小于5就切換到插入排序
- insertionSort(array, lo, hi);
- return;
- }
- int partition = partition(array, lo, hi);
- quickSort(array, lo, partition - 1);
- quickSort(array, partition + 1, hi);
- }
- //插入排序
- private void insertionSort(Comparable[] array, int lo, int hi) {
- for (int i = lo; i <= hi; i++) {
- for (int j = i; j > lo && less(array[j], array[j - 1]); j--) {
- exch(array, j, j - 1);
- }
- }
- }
三向切分 當我們需要排序的數組中出現了大量的重復元素,我們實現的快速排序在遞歸的時候會遇到許多全部重復的子數組,我們的算法依然會對其進行切分,這里有很大的提升空間。
思路就是先隨意選擇一個切分元素(el),然后把數組切換成大于、等于、小于三個部分,一次遞歸可以排定所有等于切分元素的值;維護一個指針lt、gt,使得a[lo..lt-1]都小于切分元素,a[gt+1..hi]都大于切分元素;
- 初始化變量:lt=lo, i=lo+1, gt=hi
- if a[i] < el ; 交換a[i]與a[lt], i++, lt++
- if a[i] > el ; 交換a[gt]與a[i], gt--
- a[i] == el; i++
代碼實現:
- public class Quick3waySort implements SortTemplate {
- @Override
- public void sort(Comparable[] array) {
- quickSort(array, 0, array.length - 1);
- }
- @SuppressWarnings("unchecked")
- private void quickSort(Comparable[] array, int lo, int hi) {
- if (lo >= hi) {
- return;
- }
- int lt = lo, i = lo + 1, gt = hi;
- Comparable el = array[lo];
- while (i <= gt) {
- int tmp = el.compareTo(array[i]);
- if (tmp > 0) {
- exch(array, lt++, i++);
- } else if (tmp < 0) {
- exch(array, i, gt--);
- } else {
- i++;
- }
- }
- quickSort(array, lo, lt - 1);
- quickSort(array, gt + 1, hi);
- }
- }