很多面試題的解答都是以排序為基礎的，如果我們寫出一個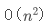的算法，大概率要被掛，今天寫個快排的基礎文章，后面看情況再把歸并和堆排序寫一寫，至于選擇排序、冒泡排序這種時間復雜度高的就不寫了，有興趣的可以找書自己看一下。

文中算法的實現是用 Go 寫了一個比較簡單的快速排序，方便大家理解(旁邊畫外音：其實是他好幾年沒面試了，太厲害的他也寫不出來)。

關于更優秀的代碼實現，可以在評論區里發出來一起學習，相信咱們讀者里一定是臥虎藏龍，有不少算法大拿。

快速排序的思想

快速排序算法首先會在序列中隨機選擇一個基準值(pivot)，然后將除了基準值之外的數分為 "比基準值小的數" 和 "比基準值大的數" 這兩個類別，再將其排列成以下形式。

【比基準值小的數】 基準值 【比基準值大的數】

接著，繼續對兩個序列 "【】"中的數據進行排序之后，整體的排序便完成了。對基準值左右兩側的序列排序時，同樣也會使用快速排序。

快速排序是一種"分治法"，將原本的問題分解成兩個子問題—— 比基準值小的數和比基準值大的數，然后再分別解決這兩個子問題。解決子問題的時候會再次使用快速排序，只有在子問題里只剩下一個數字的時候，排序才算完成。

快排的過程

下面我們用示意圖更好地理解一下快速排序對一個序列進行排序的過程。

圖例出自—《我的第一本算法書》。

假定有如下待排序序列：

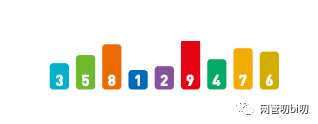
待排序序列

首先在序列中隨機選擇一個基準值，這里選擇了 4。

選擇基準值 pivot

將其他數字和基準值進行比較，小于基準值的往左移，大于基準值的往右移。

首先比較第一個元素 3 和基準值4，因為 3 < 4, 所以將 3放在基準值的左邊。

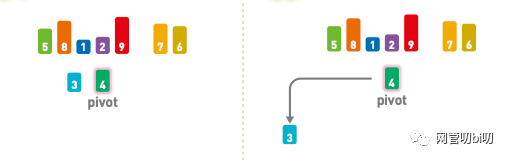
首先比較 3 和基準值4，因為 3 < 4, 所以將 3放在基準值的左邊

接下來，比較 5 和基準值，因為 5 > 4，所以將 5 放在基準值的右邊。

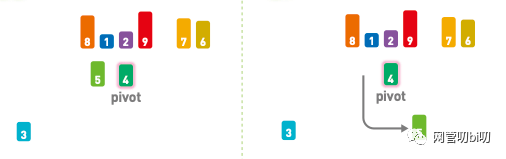
5 > 4， 將5放在基準值右邊

對整個序列進行同樣操作后，所有小于基準值的數字全都放到了基準值的左邊，大于的則全都放在了右邊。

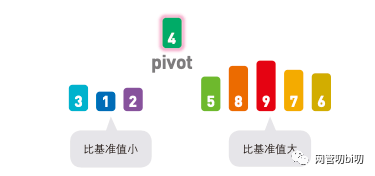
一輪排序完成后的結果

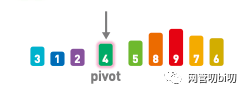
把基準值放入序列

現在排序就分成了兩個子問題，分別再對基準值左邊和右邊的數據進行排序。

分解成了兩個子問題

兩邊的排序操作也和前面的一樣，也是使用快排算法，選取基準值，把小于的數字放左邊大于的放右邊。

對子序列使用快速排序

子問題有可能會再分解成子問題，直到子問題里只剩下一個數字，再也無法分解出子問題的時候，整個序列的排序才算完成。

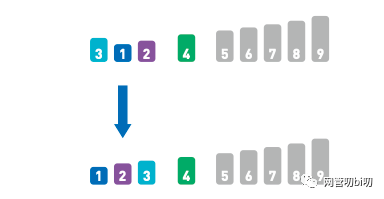
排序完成

因為快速排序算法在對序列進行排序的過程中會再次使用該算法，所以快速排序算法在實現時需要使用"遞歸”來實現。

快速排序的Go代碼實現

下面上一個用 Go 版本的快速排序算法的簡單實現：

func quickSort(sequence []int, low int, high int) {
 if high <= low {
  return
 }
 j := partition(sequence, low, high)
 quickSort(sequence, low, j-1)
 quickSort(sequence, j+1, high)
}

// 進行快速排序中的一輪排序
func partition(sequence []int, low int, high int) int {
 i, j := low+1, high
 for {
  // 把頭元素作為基準值 pivot
  for sequence[i] < sequence[low] {
   // i 坐標從前往后訪問序列，如果位置上的值大于基準值，停下來。
   // 準備和 j 坐標訪問到的小于基準值的值交換位置
   i++
   if i >= high {
    break
   }
  }
  for sequence[j] > sequence[low] {
   // j 坐標從后往前訪問序列，如果位置上的值小于基準值，停下來。
   // 和 i 坐標指向的大于基準值的值交換位置
   j--
   if j <= low {
    break
   }
  }
  if i >= j {
   break
  }
  sequence[i], sequence[j] = sequence[j], sequence[i]
 }
 sequence[low], sequence[j] = sequence[j], sequence[low]

 return j
}

每一輪快速排序都會經歷下面這幾個步驟：

1. 設置兩個變量i、j，排序開始的時候：i=0，j=待排序序列長度 - 1。
2. 以第一個數組元素作為基準值 pivot(也可以是最后一個元素，或者是隨機的一個元素)。
3. i 坐標從開始向后訪問序列里的元素，即 i++，找到第一個大于 pivot 的位置 ，和 j 坐標訪問到的小于基準值的值交換位置。
4. j 坐標從末尾向前搜索，即j--，找到第一個小于 pivot 的位置，將i，j坐標上的值進行互換。
5. 重復第3、4步，直到i=j，然后將 pivot 和 j 坐標上的值互換，完成一輪排序，小于 pivot 的值都放在了它的左邊，大于的則放到了右邊。

重復進行上面的過程，直到排序完成。最后我們可以生成一個隨機數序列對上面的快速排序函數進行測試：

func main() {
 rand.Seed(time.Now().Unix())
 sequence := rand.Perm(34)
 fmt.Printf("sequence before sort: %v", sequence)
 quickSort(sequence, 0, len(sequence) - 1)
 fmt.Printf("sequence after sort: %v", sequence)
}

快速排序的時間復雜度

分割子序列時需要選擇基準值，如果每次選擇的基準值都能使得兩個子序列的長度為原本的一半，那么快速排序的運行時間和歸并排序的一樣，都為 O(nlogn)。將序列對半分割 log2n 次之后，子序列里便只剩下一個數據，這時子序列的排序也就完成了。

因此，如果像下圖這樣一行行地展現根據基準值分割序列的過程，那么總共會有 log2n 行。

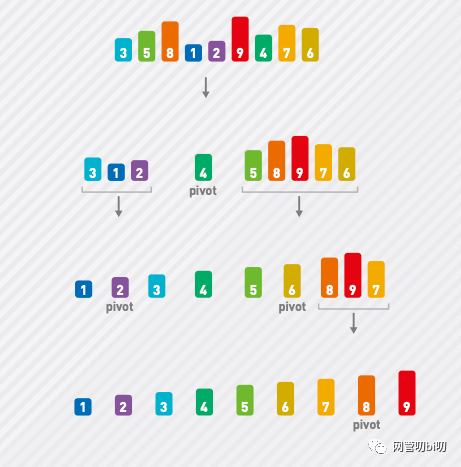
快排分解序列的次數

每行中每個數字都需要和基準值比較大小，因此每行所需的運行時間為 O(n)。由此可知，整體的時間復雜度為 O(nlogn)。

如果運氣不好，每次都選擇最小值作為基準值，那么每次都需要把其他數據移到基準值的右邊，遞歸執行 n 行，運行時間也就成了。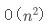

所以真正應用的時候基準值的選取也比較講究，比如以中位數做基準值：本輪排序序列的第一個、最后一個、中間位置三個數的中位數作為基準值進行排序。