人工智能算法:遺傳算法
本書的前兩章從某種抽象意義上定義了演化算法。計分、選擇、種群、交叉和突變都是演化算法的重要特點,但是我們尚未將所有這些特點整合到一個具體算法中。
遺傳算法是一種特殊的演化算法,但是在描述遺傳算法的文獻中,其定義各不相同。本書將遺傳算法定義為一種可以用交叉和突變算子優化固定長度向量的演化算法。計分函數可以區分優劣方案,以優化該固定長度的向量。這個定義說明了遺傳算法的本質。
此外,可以將可選特征添加到遺傳算法中,以增強其性能。例如物種形成、精英和其他選擇方法之類的技術,有時可以改善遺傳算法的運行效果。
3.1 離散問題的遺傳算法
與其他算法相似,針對連續學習和離散學習,遺傳算法采用略有不同的方法。連續學習涉及計算數值,而離散學習涉及識別非數值。本節將展示如何將離散學習和連續學習應用于以下兩個經典的AI問題:
旅行商問題;
鳶尾花物種建模。
對于旅行商問題,我們將展示如何將遺傳算法應用于離散學習的組合問題,目標是找到最佳的城市序列。同時,我們將擬合RBF神經網絡的權重以識別鳶尾花種類,這將作為連續問題的遺傳算法示例,即對數字權重進行調整。
3.1.1 旅行商問題
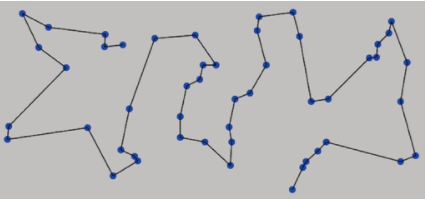
旅行商問題(Traveling Salesman Problem,TSP)涉及為旅行商確定最短路徑。旅行商必須訪問一定數量的城市,盡管他可以從任何城市開始和結束,但他只能訪問每個城市一次。TSP有多個變體,其中一些變體允許多次訪問每個城市,或為每個城市分配不同的值。本章中的TSP只是尋求一條盡可能短的路線,每個城市訪問一次。圖3-1展示了這里介紹的TSP和最短路徑。
圖3-1 旅行商問題
對于普通的迭代程序而言,找到最短的路徑似乎很容易。但是,隨著城市數量的增加,可能的組合數量也會急劇增加。如果問題有一個或兩個城市,則只能選擇一條路徑;如果包括3個城市,則可能的路徑將增加到6個。以下列表展示了路徑數量增長的速度:
1個城市有1條路徑 2個城市有2條路徑 3個城市有6條路徑 4個城市有24條路徑 5個城市有120條路徑 6個城市有720條路徑 7個城市有5 040條路徑 8個城市有40 320條路徑 9個城市有362 880條路徑 10個城市有3 628 800條路徑 11個城市有39 916 800條路徑 12個城市有479 001 600條路徑 13個城市有6 227 020 800條路徑 …… 50個城市有3.041 × 10ˆ64條路徑
在上表中,用于計算總路徑條數的公式是階乘。使用階乘運算符!作用于城市數n。某個任意值n的階乘由n×(n − 1)×(n − 2)×…×3× 2×1給出。當程序必須執行蠻力搜索時,這些值會變得非常大。TSP是“非確定性多項式時間”(non-deterministic polynomialtime,NP)難題的一個例子。“NP困難”(NP-hard)被非正式地定義為“一系列不能用暴力搜索法求解的問題”。當超過10個城市時,TSP滿足這個定義。NP困難的正式定義可以在Computers and Intractability: A Guide to the Theory of NP-Completeness [1]一書中找到。
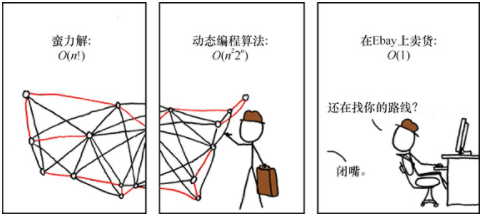
動態編程是解決TSP的另一種常用方法,如圖3-2的漫畫所示。
盡管本書沒有全面討論動態編程,但了解其基本功能還是很有價值的。動態編程將TSP之類的大問題分解為較小的問題,這項工作可以被許多較小的程序復用,從而減少蠻力解所需的迭代次數。
圖3-2 解決TSP的方法(來自xkcd網站)
與蠻力解和動態編程不同,遺傳算法不能保證找到最優解。盡管它將找到一個很好的解,但分數可能不是最好的。在3.1.2節中討論的示例程序,將展示遺傳算法如何在短短幾分鐘內為50個城市的TSP產生可接受的解 [2]。
3.1.2 為旅行商問題設計遺傳算法
TSP是最著名的計算機科學問題之一。由于傳統的迭代算法通常無法解決NP困難問題,因此程序員必須使用遺傳算法來生成潛在解。因此,我們將研究如何將遺傳算法應用于TSP。
離散遺傳算法決定了你要使用的交叉和突變算子的類型。由于離散問題是分類問題,因此你無須處理數值。所以,你可能訪問的城市就是TSP中的分類信息。按照訪問順序,城市列表是每個解的基因組。下面展示了如何表達TSP基因組:
[洛杉磯, 芝加哥, 紐約]
你的初始種群將是這些城市的隨機排列。例如,初始隨機種群可能類似于以下列表:
[洛杉磯, 芝加哥, 紐約] [芝加哥, 洛杉磯, 紐約] [紐約, 洛杉磯, 芝加哥]
你可以計算在每條路徑上行駛的英里(1英里=1 609.344米)數,從而為上述城市創建一個計分函數。考慮第一個種群成員。根據Google Maps的駕駛導航,洛杉磯至芝加哥為2 016英里,芝加哥至紐約為790英里。因此,第一個種群成員覆蓋的整個距離為2 806英里。距離是我們要最小化的分數。以上3個種群成員及其分數顯示如下。
[洛杉磯, 芝加哥, 紐約] -> 分數: 2 016 + 790 = 2 806 [芝加哥, 洛杉磯, 紐約] -> 分數: 2 016 + 2 776 = 4 792 [紐約, 洛杉磯, 芝加哥] -> 分數: 2 776 + 2 016 = 4 792
如你所見,最后兩條路徑的分數相同,因為旅行商可以從任何城市開始,所以最后兩條路徑產生相同的距離。旅行商問題的某些變體可以固定起點和終點城市。作為旅行商的家鄉,起點和終點是相同的。其他變體讓旅行商可以多次訪問同一座城市。簡而言之,如何定義旅行商問題的規則將決定如何實現計算機程序。
考慮一下這種情況:旅行商總是從同一城市(即他的家鄉)開始,并最終返回這里。在這個例子中,家鄉城市是密蘇里州的圣路易斯。此外,分數將是兩個城市間最便宜機票的價格。由于基因組仍將由洛杉磯、芝加哥和紐約的排列組成,因此圣路易斯沒有必要出現在基因組的開始和結尾。這樣可以防止算法將圣路易斯更改為不是路徑的起點或終點。換言之,計分函數隱式地將圣路易斯作為路徑的起點和終點,并對其進行適當的處理。檢查第一個種群成員,如下所示。
[洛杉磯, 芝加哥, 紐約]
該示例包括以下旅程。
圣路易斯至洛杉磯 -> 費用: $393 洛杉磯至芝加哥 -> 費用: $452 芝加哥至紐約 -> 費用: $248 紐約至圣路易斯 -> 費用: $295 總計: $1388
對問題的微小改動帶來了很大的復雜性。由于圣路易斯位于美國中部,旅行商無法再從東到西或從西到東走一條簡單的路。此外,機票價格不可互換,因為從芝加哥到圣路易斯的票價不一定與從圣路易斯到芝加哥的票價相同。旅行當天機票價格的變化使這個問題更加復雜。因此,基因組可以包括開始和結束日期。這樣,遺傳算法可以優化出行計劃和城市順序。
你還可以創建算法,以允許旅行商多次訪問同一座城市,但是,這個要求增大了計分函數的復雜性。如果你放寬要求,讓旅行商可以多次訪問同一座城市,則最佳分數可能來自以下解:
[芝加哥, 芝加哥, 芝加哥]
上述解的分數十分理想。該算法選擇了從圣路易斯到最便宜的目的地芝加哥的路徑。然后,算法再次選擇芝加哥作為第2和第3站。因為從芝加哥到芝加哥的機票是0美元,所以這次旅行的分數非常好。顯然,在這種情況下,該算法沒有為程序員做任何額外的工作。因此,計分函數需要更復雜才能傳達真正最優解的參數。也許有些城市更有價值,需要拜訪,而另一些則是可選的。設計計分函數對于遺傳算法編程至關重要。
3.1.3 旅行商問題在遺傳算法中的應用
現在,我們將看到一個簡單的遺傳算法的示例,它用一條好路徑穿過一系列城市。50個城市隨機放置在256×256網格上。該程序使用了1 000條路徑的種群,來演化出穿過這些城市的最佳路徑。因為城市列表是分類值,所以TSP是一個離散的問題。在這個示例中,計分函數計算出一條城市路徑所覆蓋的總距離,這些城市中的任何一個都不會被訪問兩次。
這些參數決定了最合適的突變和交叉算子的選擇。對于這個示例,改組突變算子是最佳選擇。如第2章所述,改組突變算子可與固定長度的分類數據配合使用。同樣,我們將使用無重復的拼接交叉算子。兩個算子都允許1 000條路徑的種群演化,并且無重復的交叉強制實現了我們的要求,即同一城市只被訪問一次。
我對該程序進行了數百次迭代,直到連續經過50次迭代而沒有出現一次改善最佳路徑長度的情況。一次迭代即經過了一個世代。程序的輸出在下面列出。
Iteration: 1 , Best Path Length = 5308.0 Iteration: 2 , Best Path Length = 5209.0 Iteration: 3 , Best Path Length = 5209.0 Iteration: 4 , Best Path Length = 5209.0 Iteration: 5 , Best Path Length = 5209.0 Iteration: 6 , Best Path Length = 5163.0 Iteration: 7 , Best Path Length = 5163.0 Iteration: 8 , Best Path Length = 5163.0 Iteration: 9 , Best Path Length = 5163.0 Iteration: 10 , Best Path Length = 5163.0 ... Iteration: 260 , Best Path Length = 4449.0 Iteration: 261 , Best Path Length = 4449.0 Iteration: 262 , Best Path Length = 4449.0 Iteration: 263 , Best Path Length = 4449.0 Iteration: 264 , Best Path Length = 4449.0 Iteration: 265 , Best Path Length = 4449.0 Good solution found: 22>1>37>30>11>33>39>24>9>16>40>3>17>49>31>48>46>20>13>47>23> 0>2>29>27>14>34>26>15>7>35>19>21>18>6>28>25>45>8>38>43>32> 41>5>10>4>44>36>12>42
如你所見,在程序確定一個解之前,發生了265次迭代。由于城市是隨機的,因此它們沒有實際名稱,而是將城市標記為“1”“2”“3”等。上面顯示的最優解從城市22開始,接下來是城市1,最終在城市42停止。你可以在以下網址查看在線的TSP實現:
http://www.heatonresearch.com/aifh/vol2/tsp_genetic.html
3.2 連續問題的遺傳算法
程序員還可以利用遺傳算法來演化連續的(即數值的)數據。在下面的示例中,我們將基于4個輸入測量值來預測鳶尾花的種類。因此,我們的遺傳算法將訓練一個徑向基函數(Radial-Basis Function,RBF)網絡模型。
模型是一種算法,它基于輸入向量進行預測,這稱為預測建模。對于鳶尾花數據集,我們將為RBF網絡提供4個描述鳶尾花的測量值。RBF網絡將根據這4個測量結果預測鳶尾花種屬。它通過訓練示例中的150朵花的數據來進行學習預測。該模型可以預測訓練集中未包含的新花的種屬。
讓我們回顧一下如何訓練模型。3個主要部分確定了遺傳算法如何訓練任何模型:
訓練設置;
超參數;
參數。
訓練設置是遺傳算法所獨有的,例如種群數量、精英數、交叉算法和突變算法。在本書的后文,我們將學習粒子群優化(PSO)和蟻群優化(ACO),它們是RBF網絡模型的訓練算法。PSO和ACO的訓練設置具有獨有的特征。程序員通常會建立訓練參數,因此,選擇最佳的參數可能需要反復試驗。
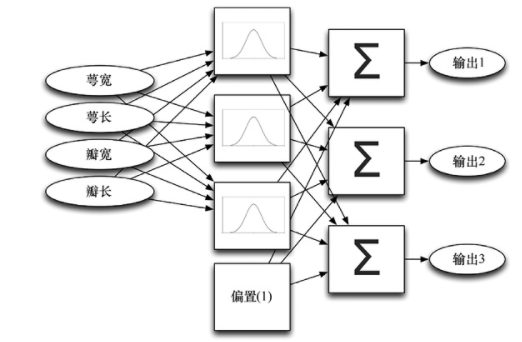
超參數定義模型的結構。考慮圖3-3,該圖展示了RBF網絡的結構。
圖3-3 以鳶尾花數據集為輸入的RBF網絡的結構
在圖3-3中,第2列顯示的是3個具有凸起形狀曲線的框,它們是RBF,使RBF網絡能夠做出預測。這個任務所需的RBF網絡的數量是一個超參數,程序員或計算機可以確定該超參數。盡管RBF數量不影響遺傳訓練,但是如果你正在使用PSO和ACO進行訓練,你仍然需要設置RBF數量。不過,你要小心,如果將RBF數量設置得太低,則創建的模型會很簡單,以至于無法從信息中學習;如果將RBF數量設置得太高,則創建的網絡會很復雜且難以訓練,并可能導致過度擬合。這是我們不希望的情況,這時模型開始將數據存儲在數據集中,而不是學習更通用的解。第10章將介紹過度擬合及其避免方法。在本章中,我們將RBF數量設置為5,這對于鳶尾花數據集似乎效果很好。我通過試驗確定了這個數字。
計算機也可以確定超參數,其中試錯法通常是找到超參數的方法。只需在1~10個RBF之間循環,并讓計算機嘗試每種情況。一旦測試了全部10個RBF,程序就會選擇獲得最佳分數的模型。該模型將告訴你RBF數量超參數的最佳設置。
最后的組成部分是參數向量。在訓練模型時,模型會調整參數向量。這方面與超參數有所不同,因為一旦訓練開始,模型就不會調整超參數。實際上,超參數定義了模型,無法更改。對參數向量進行調整是一種訓練算法(例如遺傳算法、PSO或ACO)教給模型針對給定輸入的正確響應的方法。遺傳算法利用交叉和突變來調整參數向量。
下面列出的輸出展示了使用遺傳算法針對鳶尾花數據集訓練RBF網絡的進度。如你所見,分數在前10次迭代中并沒有提高。這些迭代中的每一次迭代代表一代潛在解。分數代表錯誤分類的150朵鳶尾花的百分比,我們力求讓這個分數最小。
Iteration #1, Score = 0.1752302452792032, Species Count: 1 Iteration #2, Score = 0.1752302452792032, Species Count: 1 Iteration #3, Score = 0.1752302452792032, Species Count: 1 Iteration #4, Score = 0.1752302452792032, Species Count: 1 Iteration #5, Score = 0.1752302452792032, Species Count: 1 Iteration #6, Score = 0.1752302452792032, Species Count: 1 Iteration #7, Score = 0.1752302452792032, Species Count: 1 Iteration #8, Score = 0.1752302452792032, Species Count: 1 Iteration #9, Score = 0.1752302452792032, Species Count: 1 Iteration #10, Score = 0.1752302452792032, Species Count: 1 ... Iteration #945, Score = 0.05289116605845716, Species Count: 1 Iteration #946, Score = 0.05289116605845716, Species Count: 1 Iteration #947, Score = 0.05289116605845716, Species Count: 1 Iteration #948, Score = 0.051833695704776035, Species Count: 1 Iteration #949, Score = 0.05050776383877834, Species Count: 1 Iteration #950, Score = 0.04932340367757065, Species Count: 1 Final score: 0.04932340367757065 [- 0.55, 0.24, -0.86, -0.91] -> Iris-setosa, Ideal: Iris-setosa [-0.66, -0.16, -0.86, -0.91] -> Iris-setosa, Ideal: Iris-setosa [-0.77, 0. 0, -0.89, -0.91] -> Iris-setosa, Ideal: Iris-setosa ... [0.22, -0.16, 0.42, 0.58] -> Iris-virginica, Ideal: Iris-virginica [0.05, 0.16, 0.49, 0.83] -> Iris-virginica, Ideal: Iris-virginica [-0.11, -0.16, 0.38, 0.41] -> Iris-virginica, Ideal: Iris- virginica
在以上輸出中,你可能還看到了物種計數(species count)。由于我們目前不使用物種,因此它保持為1。第5章將介紹物種。
3.3 遺傳算法的其他應用
鳶尾花數據集和旅行商問題是人工智能文獻中的常見例子。觀察各種算法如何解決相同的問題,可以有助于理解它們的差異,檢查新問題與遺傳算法相符合的方式同樣有價值。本節將說明如何讓各種問題適應遺傳算法。
盡管本書目前未實現這些應用程序,但將來可能會包含它們。以下各小節的主要目的是演示遺傳算法在各種情況下的應用。
3.3.1 標簽云
標簽云是一種方便的工具,可用于可視化文檔中的單詞頻率計數。實際上,一個小的標簽云可以代表一個很長的文檔中的常用單詞,但是,標簽云算法通常會從單詞數統計中刪除結構化單詞(例如“the”)。圖3-4展示了根據《人工智能算法(卷1):基礎算法》英文版創建的標簽云。
圖3-4 卷1的標簽云
圖3-4所示的標簽云展示了每個單詞出現的頻率。你可以輕松地看到,“algorithm”是卷1中最常見的單詞。
要創建標簽云,必須統計單詞數。下面展示了構建圖3-4所示標簽云的單詞計數:
341 algorithm 239 training 203 data 201 output 198 random 192 algorithms 169 number 163 input ...
單詞計數提供每個單詞的出現頻率,并與其他單詞對比。標簽云中的單詞互相交織,使得單詞之間的空白空間最小。在示例中,較小的單詞填充了“algorithm”的“h”和“m”下的空白。
創建標簽云的第一步是選擇一些單詞并確定它們的大小。上面的單詞計數說明了這個步驟。最有可能的是,你會在標簽云中包含文檔中大約100個最常見的單詞。標簽云中的確切字數將根據顯示美觀度進行調整。單詞在文本中出現的次數將決定單詞的大小。
消除空白是遺傳算法的一項重要應用。x和y坐標、方向指示共同代表了每個單詞。其中x和y坐標表明每個單詞在顯示屏上的位置,方向指示表明單詞是水平的還是垂直的。這3個數據項產生的向量長度等于標簽云中單詞數量的3倍。如果顯示100個單詞,則向量的長度為300個元素。對于空白和重疊文本,基因組將接受罰分。標簽云不應該有重疊的文本。因此,你需要創建類似于以下內容的計分函數:
[空白像素數] + ([重疊像素數] × 100)
遺傳算法應設法最小化這個計分函數。如果文本重疊,則需要增加系數100。
3.3.2 馬賽克藝術
藝術生成是遺傳算法的另一個非常常見的例子。編寫計算機藝術的計分函數非常容易。你需要將源圖像與遺傳算法創建的圖像進行比較;還要為遺傳算法提供一組工具,以便它可以生成圖像并顯示其模擬的創造力。
人類畫家的工作方式基本相同。顯然,產生圖像的最簡單方法是用數碼相機照相,但是,畫家用自己的工具(畫筆和顏料)創造了藝術。對于遺傳算法,工具是編程語言的圖形命令,計分函數只是將原始圖像與遺傳算法產生的圖像進行比較。例如,你可以限制遺傳算法,讓它僅用少數幾種顏色畫圓。僅使用程序中允許的元素,遺傳算法將通過演化,產生原始照片的最佳渲染效果。通過這種方式,它展示了模擬的創造力。
用遺傳算法創建計算機藝術的一個例子是馬賽克,它是由較小圖像集合組成的較大圖像。主圖像包含一個圖像網格,較小的圖像將放置在每個網格單元中。圖3-5展示了一幅馬賽克。
圖3-5 玄鳳鸚鵡馬賽克
圖3-5描繪了由動物圖像生成的玄鳳鸚鵡馬賽克。玄鳳鸚鵡的圖像尺寸為2 048像素×2 048像素,每張尺寸為32像素×32像素的較小動物圖像的網格將構成該馬賽克。將這些較小的動物圖像的網格覆蓋到較大的圖像上,則將形成64×64的網格。(圖3-5經過裁剪,僅展示其中一部分。)選擇一組較小的動物圖像放入64×64的網格中,使得網格在整體上可以最佳地呈現出一只玄鳳鸚鵡的樣子。
每個基因組都是固定長度的數組,長度等于64×64即4 096字節。使用計分函數比較生成的馬賽克圖像和原始圖像之間的差異。一旦得分降到最低,你將擁有與玄鳳鸚鵡非常相似的馬賽克。
3.4 本章小結
遺傳算法利用種群、計分、交叉和突變來解決實際的編程問題。遺傳算法是在第1章和第2章中學到的概念的具體實現,這些概念與交叉和突變一起工作,可以為下一代提供更好的解。
遺傳算法要求解以固定長度數組表示。這項要求似乎很有局限性,但是許多解都可以用這種方式表示。在本章中,我們還演示了旅行商問題和鳶尾花數據集。另外,我們討論了遺傳算法如何應用于標簽云和馬賽克藝術。
為了超越定長數組,第4章將介紹如何演化實際的程序。實際上,遺傳編程可以將計算機程序表示為樹狀結構,以便為下一代創建更好的程序。