譯者 | 布加迪

審校 | 重樓

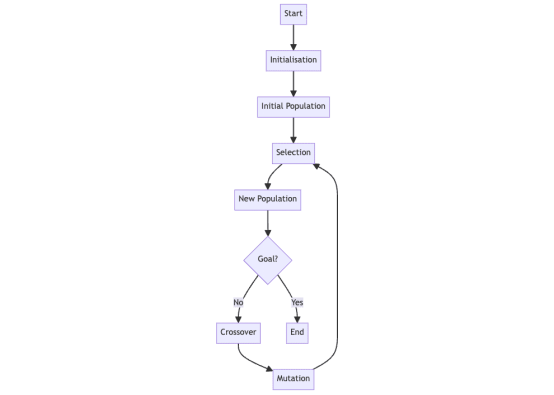
遺傳算法是一種基于自然選擇的技術(shù)，用于解決復雜問題。由于問題很復雜，遺傳算法（而不是其他方法）被用來得出解決問題的合理方案。本文介紹遺傳算法的基礎知識以及如何用Python來實現(xiàn)。

遺傳算法的要素

適應度函數(shù)

適應度函數(shù)衡量所考慮的解決方案與問題的最佳解決方案的接近程度。它為人群中的每個人提供了適應度水平，描述了當前一代人的質(zhì)量或效率。這個分值定義了選擇，而更高的適應度值表明是經(jīng)過優(yōu)化的解決方案。

比如說，假設我們在處理一個實際的函數(shù)f(x)，其中x是一組參數(shù)。要找到的最優(yōu)值是x，這樣f(x)就取最大值。

選擇

這個過程決定了當前一代人中哪些個體受到青睞，從而繁殖、為下一代做出貢獻。可以確定許多選擇方法，每種方法都有自己的特點和適合的上下文。

• 輪盤選擇：

根據(jù)個體的適應度水平，選擇個體的概率也是最大的。

• 錦標賽選擇：

隨機抽取一組，選擇其中最好的。

• 基于排序的選擇：

根據(jù)適合度對人進行排序，選擇機會則根據(jù)適合度分數(shù)按比例分配。

交叉

交叉是遺傳算法的一個基本概念，其目的是交換兩個親本的遺傳信息，形成一個或多個后代。這個過程非常類似自然界中發(fā)生的生物的交叉和重組。運用遺傳的基本原理，交叉試圖產(chǎn)生具有雙親理想特征的后代，從而在下一代中有更好的適應性。交叉是一個比較寬泛的概念，可以分為幾種類型，每種類型都有其特點和可以有效運用的領域。

• 單點交叉：在親本染色體上選擇一個交叉點，實際上只發(fā)生一次交叉。這個位置之前的所有基因都取自第一個親本，而這個位置之后的所有基因都取自第二個親本。
• 兩點交叉：選擇兩個斷點，它們之間的部分在兩個親本染色體之間交換。它也有利于遺傳信息的交換，這與單點交叉不一樣。

突變

在遺傳算法中，突變之所以至關(guān)重要，是由于它提供了多樣性，多樣性是避免直接向最優(yōu)解區(qū)域收斂的關(guān)鍵因素。因此，獲得單個突變基因串的隨機變化，算法可以進入僅通過交叉操作無法企及的最優(yōu)解空間的其他區(qū)域。這個隨機過程保證了無論怎樣，人群都會進化，或者在遺傳算法確定的搜索空間區(qū)域內(nèi)移動其位置。

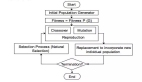
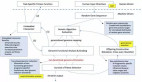
實現(xiàn)遺傳算法的步驟

不妨用Python實現(xiàn)遺傳算法。

問題定義

問題：對具體函數(shù)進行計算；f (x) = x^2f(x) = x^2，只對x值取整。

適應度函數(shù)：對于染色體二進制為x的情況，適應度函數(shù)的一個例子可能是f(x)= x^2。

def fitness(chromosome):
  x = int(''.join(map(str, chromosome)), 2)
 return x ** 2

人群初始化

生成一個給定長度的隨機染色體。

def generate_chromosome(length):
 return [random.randint(0, 1) for _ in range(length)]

def generate_population(size, chromosome_length):
 return [generate_chromosome(chromosome_length) for _ in range(size)]

population_size = 10
chromosome_length = 5
population = generate_population(population_size, chromosome_length)

適應度評估

評估人群中每個染色體的適應度。

fitnesses = [fitness(chromosome) for chromosome in population]

選擇

使用輪盤選擇法根據(jù)適合度選擇親本染色體。

def select_pair(population, fitnesses):
   total_fitness = sum(fitnesses)
 selection_probs = [f / total_fitness for f in fitnesses]
   parent1 = population[random.choices(range(len(population)), selection_probs)[0]]
 parent2 = population[random.choices(range(len(population)), selection_probs)[0]]
 return parent1, parent2

交叉

使用單點交叉，在父本基因串中選擇一個隨機的交叉位置，并在兩個基因串之間交換這個位置之后的所有基因值。

def crossover(parent1, parent2):
 point = random.randint(1, len(parent1) - 1)
 offspring1 = parent1[:point] + parent2[point:]
 offspring2 = parent2[:point] + parent1[point:]
 return offspring1, offspring2

突變

通過以一定的概率翻轉(zhuǎn)比特來實現(xiàn)突變。

def mutate(chromosome, mutation_rate):
 return [gene if random.random() > mutation_rate else 1 - gene for gene in chromosome]

mutation_rate = 0.01

結(jié)語

總之，由于模擬物種進化，遺傳算法對于解決無法直接解決的優(yōu)化問題具有一致性和有效性。因此，一旦您掌握了遺傳算法的基本要素，并了解了如何用Python實現(xiàn)遺傳算法，解決復雜任務就會容易得多。選擇、交叉和突變使您能夠?qū)鉀Q方案進行修改，并不斷獲得最佳或接近最佳的答案。但愿您已準備好將遺傳算法運用到自己的任務中，從而在不同的任務和問題解決中得到改進。

原文標題：Understanding and Implementing Genetic Algorithms in Python，作者：Jayita Gulati